数论-组合数

Posted 2021-03-11 sxq-study

组合数一：

组合数范围小，询问多，可以采用预处理方式，把所有的都处理出来

题目：

给定nn组询问，每组询问给定两个整数a，ba，b，请你输出Cba mod (109+7)Cab mod (109+7)的值。

输入格式

第一行包含整数nn。

接下来nn行，每行包含一组aa和bb。

输出格式

共nn行，每行输出一个询问的解。

数据范围

1≤n≤100001≤n≤10000,
1≤b≤a≤20001≤b≤a≤2000

输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

 1 #include <iostream>
 2 using namespace std;
 3 
 4 const int N = 2010;
 5 const int mod = 1e9+7;
 6 
 7 int c[N][N];
 8 
 9 void init(){
10     for(int i = 0;i < N;++i)
11         for(int j = 0;j <= i;++j)
12             if(j == 0) c[i][j] = 1;
13             else c[i][j] = (c[i-1][j-1] + c[i-1][j]) % mod;//记住这个公式
14 }
15 
16 int main(){
17     init();
18     int n;cin >> n;
19     while(n --){
20         int a, b;cin >> a >> b;
21         cout << c[a][b] << endl;
22     }
23     return 0;
24 }

View Code

 

组合数二：

组合数范围大，询问也很多，可以采用组合数公式，此时需要用到乘法逆元

题目：

给定nn组询问，每组询问给定两个整数a，ba，b，请你输出Cba mod (109+7)Cab mod (109+7)的值。

输入格式

第一行包含整数nn。

接下来nn行，每行包含一组aa和bb。

输出格式

共nn行，每行输出一个询问的解。

数据范围

1≤n≤100001≤n≤10000,
1≤b≤a≤1051≤b≤a≤105

输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

 1 #include <iostream>
 2 using namespace std;
 3 
 4 typedef long long ll;
 5 const int N = 1e5+10;
 6 const int mod = 1e9+7;
 7 
 8 ll fact[N], infact[N];//fact存的是阶乘，infact存的是阶乘的逆元
 9 
10 ll qmi(ll a, ll k, ll p){
11     ll res = 1;
12     while (k)
13     {
14         if (k & 1) res = res * a % p;
15         a = a * a % p;
16         k >>= 1;
17     }
18     return res;
19 }
20 
21 int main(){
22     fact[0] = infact[0] = 1;
23     for(int i = 1;i < N;++i){
24         fact[i] = i * fact[i - 1] % mod;
25         infact[i] = qmi(fact[i], mod - 2, mod) % mod;
26     }
27     int n;cin >> n;
28     while(n --){
29         int a, b;cin >> a >> b;
30         cout << fact[a]*infact[b]%mod*infact[a-b]%mod << endl;
31     }
32     return 0;
33 }

View Code

 

组合数三：

询问少，但是组合数范围巨大，采用卢斯卡定理，

组合数定义式：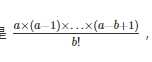       

 

 

题目：

给定nn组询问，每组询问给定三个整数a,b,pa,b,p，其中pp是质数，请你输出Cba mod pCab mod p的值。

输入格式

第一行包含整数nn。

接下来nn行，每行包含一组a,b,pa,b,p。

输出格式

共nn行，每行输出一个询问的解。

数据范围

1≤n≤201≤n≤20,
1≤b≤a≤10181≤b≤a≤1018,
1≤p≤1051≤p≤105,

输入样例：

3
5 3 7
3 1 5
6 4 13

输出样例：

3
3
2

 1 #include <iostream>
 2 using namespace std;
 3 
 4 typedef long long ll;
 5 
 6 ll qmi(ll a, ll k, ll p){
 7     ll res = 1;
 8     while (k)
 9     {
10         if (k & 1) res = res * a % p;
11         a = a * a % p;
12         k >>= 1;
13     }
14     return res;
15 }
16 
17 ll C(ll a, ll b, ll p){
18     if(b > a) return 0;
19     ll x = 1, y = 1;
20     for(int i = 0; i < b; i++)//定义式
21     {
22         x = x * (a - i) % p;
23         y = y * (i + 1) % p;
24     }
25     return x * qmi(y, p - 2, p) % p;//x是分子，y是分母，分母用到了逆元
26 }
27 
28 ll lusca(ll a, ll b, ll p){
29     if(a < p && b < p) return C(a, b, p);
30     return C(a%p, b%p, p) * lusca(a/p, b/p, p) % p;//公式
31 }
32 
33 int main(){
34     int n;cin >> n;
35     while(n --){
36         ll a, b, p;cin >> a >> b >> p;
37         cout << lusca(a, b, p) << endl;
38     }
39     return 0;
40 }

View Code

 

组合数四：

求出来的结果很大，需要用到高精度

题目：

输入a,ba,b，求CbaCab的值。

注意结果可能很大，需要使用高精度计算。

输入格式

共一行，包含两个整数aa和bb。

输出格式

共一行，输出CbaCab的值。

数据范围

1≤b≤a≤50001≤b≤a≤5000

输入样例：

5 3

输出样例：

10

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 const int N = 5010;
 5 
 6 int prime[N], cnt;
 7 bool st[N];
 8 int sum[N];
 9 
10 
11 void get_prime(int n){
12     for(int i = 2;i <= n;++i){
13         if(!st[i]){
14             prime[cnt++] = i;
15             for(int j = i + i;j <= n;j += i) st[j] = true;
16         }
17     }
18 }
19 //看a的阶乘里有多少个p
20 int get(int a, int p){
21     int res = 0;
22     while(a){
23         res += a / p;
24         a /= p;
25     }
26     return res;
27 }
28 //高精度乘法
29 vector<int> mul(vector<int>& a, int b){
30     vector<int> res;
31     int t = 0;
32     for(int i = 0;i < a.size();++i){
33         t += a[i] * b;
34         res.push_back(t % 10);
35         t /= 10;
36     }
37     while(t){
38         res.push_back(t % 10);
39         t /= 10;
40     }
41     return res;
42 }
43 
44 int main(){
45     int a, b;cin >> a >> b;
46     get_prime(a);//获取所有质数
47     //枚举每个质数，看看结果里有多个该质数
48     for(int i = 0;i < cnt;++i){
49         int t = prime[i];
50         sum[i] = get(a, t) - get(b, t) - get(a - b, t);
51     }
52     //求结果
53     vector<int> ans; 
54     ans.push_back(1);
55     for(int i = 0;i < cnt;++i)
56         for(int j = 0;j < sum[i];++j)
57             ans = mul(ans, prime[i]);
58         
59     for(int i = ans.size()-1;i >= 0;--i) printf("%d", ans[i]);
60     return 0;
61 }

View Code