HDU-4857 逃生（逆向拓扑排序）

Posted 2021-03-09 jiamian

 

Problem Description

糟糕的事情发生啦，现在大家都忙着逃命。但是逃命的通道很窄，大家只能排成一行。

现在有n个人，从1标号到n。同时有一些奇怪的约束条件，每个都形如：a必须在b之前。
同时，社会是不平等的，这些人有的穷有的富。1号最富，2号第二富，以此类推。有钱人就贿赂负责人，所以他们有一些好处。

负责人现在可以安排大家排队的顺序，由于收了好处，所以他要让1号尽量靠前，如果此时还有多种情况，就再让2号尽量靠前，如果还有多种情况，就让3号尽量靠前，以此类推。

那么你就要安排大家的顺序。我们保证一定有解。

 

 

Input

第一行一个整数T(1 <= T <= 5),表示测试数据的个数。
然后对于每个测试数据，第一行有两个整数n(1 <= n <= 30000)和m(1 <= m <= 100000)，分别表示人数和约束的个数。

然后m行，每行两个整数a和b，表示有一个约束a号必须在b号之前。a和b必然不同。

 

Output

对每个测试数据，输出一行排队的顺序，用空格隔开。

Sample Input

1
5 10
3 5
1 4
2 5
1 2
3 4
1 4
2 3
1 5
3 5
1 2

Sample Output

1 2 3 4 5

 

 

这是一种比较坑的排序，要求编号小的尽量排在前面，这里平时的是不一样的。

 

例子来自：https://blog.csdn.net/qq_41713256/article/details/80805338

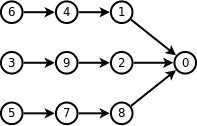
如果你用优先队列拓扑排序得到的是：3 5 6 4 1 7 8 9 2 0

但是正确答案为 6 4 1 3 9 2 5 7 8 0 这样使得小的（1）尽量在前面。

 

这题相当于逆向的拓扑排序，因为小的要尽量放前面。

如果正向拓扑的话，优先队列要设置成小的值优先，这样万一出现一个比较小的入度为0的点，就会直接放进queue去 ，这样万一后面还有更小的点的话就出错了。

所以要逆向拓扑，从右往左想，所有特殊条件都没有指明谁要在它后面的点先放（即这个点的出度为0），优先队列设置成大的优先。

 

思路：逆向拓扑 + 优先队列

1.反向建边,点大的优先级高。
2.用拓扑排序+优先队列，逆向输出序列即可。

 

 

 1 #include <stdio.h>
 2 #include <string.h>
 3 #include <iostream>
 4 #include <string>
 5 #include <math.h>
 6 #include <algorithm>
 7 #include <vector>
 8 #include <stack>
 9 #include <queue>
10 #include <set>
11 #include <map>
12 #include <sstream>
13 const int INF=0x3f3f3f3f;
14 typedef long long LL;
15 const double eps =1e-8;
16 const int mod=1e9+7;
17 const int maxn=1e5+10;
18 using namespace std;
19 
20 struct edge
21 {
22     int to;
23     int next;
24 }E[maxn];
25 int head[maxn];
26 int tot;
27 void add(int u,int v)
28 {
29     E[tot].to=v;
30     E[tot].next=head[u];
31     head[u]=tot++;
32 } 
33 
34 priority_queue<int> qe;
35 vector<int> ans;
36 int in[maxn];
37 
38 void init()
39 {
40     tot=0;
41     memset(in,0,sizeof(in));
42     memset(head,-1,sizeof(head));
43     while(!qe.empty()) qe.pop();
44     ans.clear();
45 }
46 
47 int main()
48 {
49     #ifdef DEBUG
50     freopen("sample.txt","r",stdin);
51     #endif
52     
53     int T;
54     scanf("%d",&T);
55     while(T--)
56     {
57         int n,m;
58         scanf("%d %d",&n,&m);
59         init();
60         for(int i=1;i<=m;i++)
61         {
62             int u,v;
63             scanf("%d %d",&u,&v);
64             add(v,u);
65             in[u]++;
66         }
67         for(int i=1;i<=n;i++)
68             if(in[i]==0) qe.push(i);
69         while(!qe.empty())
70         {
71             int u=qe.top(); qe.pop();
72             ans.push_back(u);
73             for(int i=head[u];i!=-1;i=E[i].next)
74             {
75                 int v=E[i].to;
76                 in[v]--;
77                 if(in[v]==0) qe.push(v);
78             }
79         }
80         for(int i=ans.size()-1;i>=0;i--)
81             printf(i==0?"%d
":"%d ",ans[i]);
82     } 
83         
84     return 0;
85 }

 

 

 

-