《概率统计》理论基石：条件概率独立性与贝叶斯

Posted 2021-03-03 traditional

从概率到条件概率

对于概率，相信大家都不会陌生，在各阶段的数学课上，它都是高频出现的常客，最简单的概率场景比如掷骰子：第一次掷出的点数为 5 的概率为多大？你会毫不犹豫的说出答案：1/6。

这太简单了。接下来我增加一个限定条件：已知在抛出骰子是奇数的情况下，抛掷点数为 5 的可能性有多大？

发现了没有，在第二个问题中我就没有直接地只问投掷出 5 这个事件的概率，而是增加了一个前提条件：这次抛掷出的点数为奇数。

生活中这类场景更多，我们一般不会直接去推断一个事件发生的可能性，因为这样实际意义并不明显，而且也不容易推断出结果。比如我问你今天下雨的概率是多大？你可能是一头雾水，什么地点？什么月份？当日云层的厚度？这些条件都没有提供，这样是无法给出一个有意义、有价值的合理推断的。

而且在实际情况下，一个事件一般而言也不会是孤立的发生，它会伴随着其他事情一同出现，单独谈一个事件的概率，一般而言也是不存在的。

因此，在实际的应用中，我们更关心的是条件概率，也就是在给定部分信息的基础上对试验结果的推断。这些给定的信息就是我们附加的条件，是我们研究时关注的重点。这里，我们来具体描述一下条件概率：

假设我们知道给定事件 B 已经发生，在此基础上希望知道另一个事件 A 发生的可能性，此时我们就需要构造出 条件概率，它需要先顾及事件 B 已经发生的信息，然后再求出事件 A 发生的概率。

这个条件概率描述的就是在给定事件 B 发生的情况下，事件 A 发生的概率，我们专门把它记作：P(A|B)。

那我们回到投掷骰子的问题中来，在投出奇数点数骰子的前提下，投出 5 的概率有多大？奇数点数一共有 {1,3,5} 三种，其中出现 5 的概率是 1/3。很明显，和单独问投出点数是 5 的概率计算结果是不同的。

条件概率表达式

先看一张图：

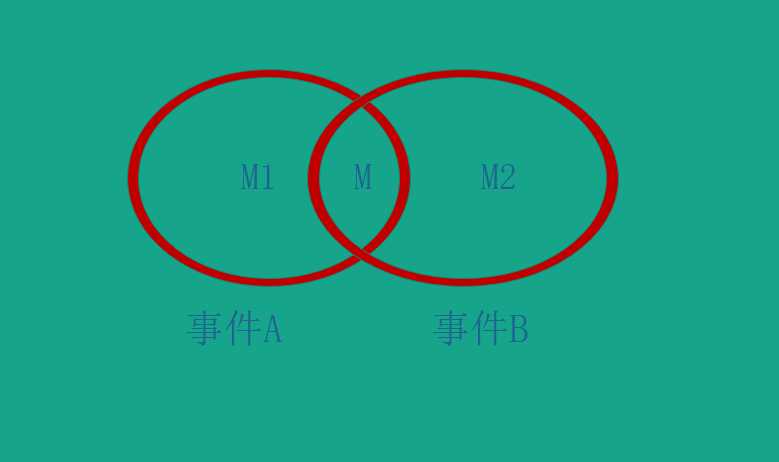
我们做一个实验，实验的结果要么发生事件A、要么发生事件B，当然结果也可能既是事件A、又是事件B，这两个事件之间存在交集。

然后我们做了N次实验，其中有M1次发生了事件A、M2次发生事件B，M次两个事件都发生。所以实际上总次数N=M1+M2-M，但是现在我问你，单纯的事件A和事件B发生的概率是多少？你肯定会脱口而出：分别是M1/N、M2/N。那么再代入到条件概率中来，已知在事件B发生的前提下，事件A发生 的概率是多少呢？

首先我们要求的是事件A发生的前提是事件B发生，所以我们是在B发生的前提下计算A发生的概率，那么样本总数就不再是N了，而是M2。而在事件B发生的前提下事件A再发生，那不就是两者同时发生吗？所以显然总共出现了M次，那么答案就很明显了。

在事件B发生的前提下，事件A发生的概率就是P(A|B) = M / M2

我们说上面的M和M2指的是发生的次数，我们可以进一步推导：

对于M / M2，我给分子分母同时除以一个初始的样本总数N，所以P(A|B) = (M / N) / (M2 / N) = P(AB) / P(B)

因此我们得到了一个更具有一般性的结论，那就是在B发生的前提下A发生的概率等于AB同时发生的概率除以B发生的概率。

两个事件的独立性

在上面的例子中，我们看到事件A的无条件概率P(A)和在事件B发生的前提下A发生的概率P(A|B)一般是不一样的，这也是普遍存在的一种情况。但是两者之间的关系还是能说明一些问题的：

• P(A) < P(A|B)：它反映了事件B如果发生了，那么事件A更有可能发生。还是掷骰子，A表示出现数字5的概率、B表示出现奇数的概率。如果事件B发生，那么代表点数是奇数，相当于将样本范围进一步缩小了。

• P(A) = P(A|B)：它反映了事件B的发生跟事件A是否发生没有任何关系，我们计算A发生的概率，可以无视事件B。比如：明天京东上某个商品是否降价和广州是否下雨之间没有关系，广州下不下雨对商品降价无影响。

  此时我们称A和B是独立事件，我们由P(A|B)=P(AB)/P(B)可以得到，P(AB)=P(A|B)·P(B)，即A和B同时发生的概率等于B发生的概率乘上在B发生的前提下A发生的概率或者等于A发生的概率乘上在A发生的前提下B发生的概率，这两者是一样的。但如果A和B之间是独立的，那么A和B同时发生的概率就等于A发生的概率乘上B发生的概率。

• P(A) > P(A|B)：它反映了B发生了会降低A发生的可能性，比如从1到10之间随机选择一个数，事件A表示选择的数字大于等于7，那么无条件概率就是4 / 10 = 0.4；但是B表示抽中的数字小于等于7，如果B发生了那么A再发生的话，数字就只能是7，所以概率变成1 / 7

  因此我们看到P(A)和P(A|B)之间关系的不同，能反映出A和B两个事件的关系，当然我们这里不考虑那种偶然性，而是考虑一种普遍性。所以即便广州下雨了、京东的某个商品也降价了，但两者还是没有关系，因为我们考虑的是一种具有普遍性的结论。

• P(A|B) = 0：它反映了事件B一旦发生了，事件A就不可能再发生，这算是P(A) > P(A|B)的特例吧，虽然概率降低了，但是还有可能发生。而P(A|B)=0则是说明了B发生了A就不可能再发生了，所以我们称此时的A和B为互斥事件

因此针对事件发生的可能性、以及事件之间的关系，我们对事件也有几个分类：

• 随机事件：一个事件可能发生、也可能不发生，那么这个事件就叫做随机事件。比如：漫展上一个皮肤白皙、长相可爱的人是女性，这就是个随机事件，因为还有可能是个女装大佬，这谁说的准呢
• 不可能事件：一个事件一定不会发生，那么这个事件就叫做不能事件。比如：从1到10中选择一个大于20的数
• 必然事件：一个事件一定会发生，那么这个事件就叫做必然事件。比如：太阳从东方升起
• 互斥事件：不可能同时发生的两个事件就是互斥事件。即：A发生B不发生、B发生A不发生、A和B都不发生
• 对立事件：不可能同时发生、但是一定会发生其中一个的两个事件就是互斥事件。即：A发生B不发生，B发生A不发生，只有这两种情况。

全概率公式

假设有n个事件B1、B2、B3...Bn，它们之间两两互斥、且至少发生一个，那么对于任意的事件A，都有如下关系：

P(A) = P(B1)P(A|B1) + P(B2)P(A|B2)+...+P(Bn)P(A|Bn)

我们来解释一下：首先我们说n个事件是两两互斥，且至少发生一个。那么我们先假设只有一个事件B1，如果是只是一个事件B1、且B1必发生，那么有P(A)=P(B1)P(A|B1)显然是没问题的，因为B1一定发生，所以就不考虑了。

然后扩展到n个事件，我们说是两两互斥、且必发生一个，那么肯定有P(B1) + P(B2) + P(B3) + ... +P(Bn)=1?

P(A) = P(A · 1)

P(A) = P(AB1 + AB2 + AB3 + ... ABn)

因为事件B1、B2、B3...Bn两两互斥，所以AB1、AB2、AB3...ABn也是两两互斥，那么有：

P(A) = P(AB1) + P(AB2) + P(AB3) + ... + P(ABn)

我们是对于任意事件A，所以A和B1、B2、B3...Bn之间的关系是不清楚的，所以得到：

P(A) = P(B1)P(A|B1) + P(B2)P(A|B2)+...+P(Bn)P(A|Bn)

所以P(A) = P(B1)P(A|B1) + P(B2)P(A|B2)+...+P(Bn)P(A|Bn)我们就称之为全概率公式

全概率公式的实际价值就在于，我们想计算事件A的概率是比较困难的。但如果条件概率P(A|Bn)是已知的，则变得很好计算，因此此时全概率公式就成了计算P(A)的很好途径。

聚焦贝叶斯公式

我们之前说了：P(AB) = P(A)P(B|A) = P(B)P(A|B)，那么在了解完全概率公式之后，我们可以将两者组合起来，得到如下的式子：

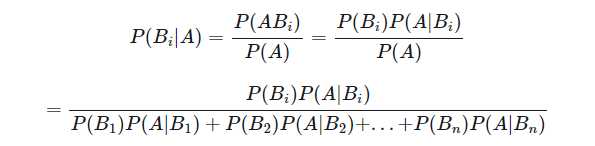
于是我们就得到了大名鼎鼎的贝叶斯公式，我们先不管下面的那一大长串，我们上面的很好理解。然后下面的一大长串，就是将分母的P(A)用全概率公式进行了替换。而分子上则不再是B，而是Bi。其中Bi则指的是下面B1、B2、B3...Bn之一，因为我们使用贝叶斯的场景一般都是：导致这个结果的原因可能有多种，但不知具体是哪一种，所以用贝叶斯来分析每一种的概率有多大，我们后面会举例说明。

可能这个式子看起来平淡无奇，但里面包含了很多内容，我们来分析一下：

首先贝叶斯公式最根本的数学基础就是它将P(A|B)和P(B|A)联系了起来。

我们说P(A|B)P(B)和P(B|A)P(A)两者是相等的，它们都等于P(AB)，里面的内涵是什么，我们往下看。

这个简单的等式的内涵就在于：由因到果、由果推因。

现实中，我们可以把A看成是结果，B1、B2、B3...Bn看成是导致这个结果的原因

那么我们说的全概率公式，就是由各种原因推理出结果事件发生的概率，由因到果

但是，更重要、更实际的应用场景是，我们在日常生活中常常是观察到某种现象，然后去反推造成这种现象的各种原因的概率。简单点说，就是由果推因。

贝叶斯公式P(Bi|A)=...，最终求得的就是条件概率。在结果事件A发生的前提下，我们推断结果事件A的发生(在众多原因B1、B2、B3...Bn中)是由原因Bi(i=0,1,2...n)造成的概率有多大，以支撑我们后续判断。

那么我们说单纯的概率：P(Bi)叫做先验概率，指的是在没有别的前提信息情况下的概率值，这个值一般需要借助我们的经验估计得到。

而P(Bi|A)叫做后验概率，它表示在得到某个信息之后事件出现的概率值，可以说后验概率是先验概率在获取了新信息之后的一种修正。

应用举例

贝叶斯应用

比如，贝叶斯公式应用的一个常见例子就是 X 光片的病理推断案例，在某个病人的 X 光片中，医生看到了一个阴影，这就是结果事件 A，我们希望对造成这个结果的三种可能原因（原因 B1：恶性肿瘤；原因 B2：良性肿瘤；原因 B3：其他原因）进行分析判断，推断分属于各个原因的概率

例如，我们想求出原因是恶性肿瘤的概率，也就是求条件概率：P(B1|A) 的值。而我们只要知道在这三种原因下出现阴影的概率，也就是 P(A|B1)，P(A|B2)，P(A|B3)，以及三种原因的先验概率：P(B1)，P(B2)，P(B3)，就能通过贝叶斯公式：

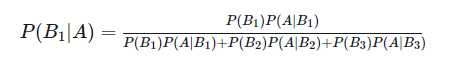
来进行计算。我们说导致X光片中出现阴影的原因有三种，但是不知道是三种的哪一种，所以使用贝叶斯来推断是第一种恶性肿瘤的原因的可能性有多大。所以贝叶斯定义就是P(B|A)P(A)?=?P(A|B)P(B)和全概率公式P(A)=P(B1)P(A|B1) + P(B2)P(A|B2)+...+P(Bn)P(A|Bn)两者的组合，把等式P(B|A)P(A) = P(A|B)P(B)左边的P(A)移到右边分母上，再用全概率公式P(A) = P(B1)P(A|B1) + P(B2)P(A|B2)+...+P(Bn)P(A|Bn)进行替换即可得到贝叶斯公式。只不过前面的不再是P(B|A)，而是P(Bi|A)，Bi为B1、B2...Bn之一。

条件概率应用

这个应用没有涉及到贝叶斯，只是单纯地考察P(A|B)P(B)=P(B|A)P(A)

已知：新垣结衣明天有百分之60的概率不结婚，如果结婚了那么有百分之50的概率和我结婚。

• 问题一：明天新垣结衣和我结婚的概率是多少？
• 问题二：已知明天我没和新垣结衣结婚，那么新垣结衣明天结婚的概率是多少？

解答问题一：

很简单，和我结婚的前提，是明天新垣结衣得结婚才行。结婚的概率是4/10，百分之五十的概率和我结婚，所以概率是1/5

解答问题二：

明天我没和新垣结衣结婚有两种可能，第一：新垣结衣没结婚，第二：结婚了但是和别人结婚了。我们要求出新垣结衣结婚的概率，假设事件A：新垣结衣明天结婚，事件B：新垣结衣没和我结婚。显然B已经发生了，我们目的是求出在B发生的情况下A发生的概率

P(A|B)就是我们要求的概率，显然有：P(A|B) = P(AB) / P(B)，对于P(AB)显然等于4/10 * 1/2?==?1/5，而P(B)表示新垣结衣不和我结婚，那么有两种情况，不结婚(6/10),和别人结婚(2/10),相加是8/10= 4/5，所以P(A|B) = 1/5 / 4/5 = 1/4，因此明天新垣结衣结婚的概率是1/4