动态规划（上）：如何实现基于编辑距离的查询推荐？

Posted 2021-03-01 liugangjiayou

动态规划（上）：如何实现基于编辑距离的查询推荐？

什么是动态规划呢？

我们需要在各种可能的局部解中，找出那些可能达到最优的局部解，而放弃其他的局部解。这个寻找最优解的过程其实就是动态规划。

动态规划需要通过子问题的最优解，推导出最终问题的最优解，因此这种方法特别注重子问题之间的转移关系。我们通常把这些子问题之间的转移称为状态转移，并把用于刻画这些状态转移的表达式称为状态转移方程。很显然，找到合适的状态转移方程，是动态规划的关键。

编辑距离

当你在搜索引擎的搜索框中输入单词的时候，搜索引擎会返回一系列相关的关键词，方便你直接点击。

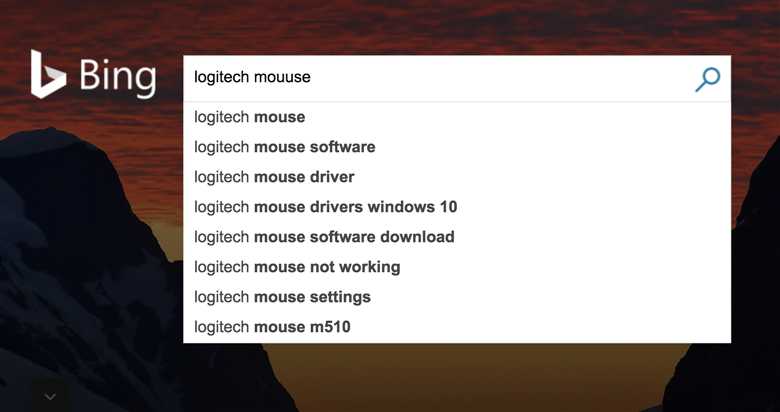
搜索下拉提示和关键词纠错，这两个功能其实就是查询推荐。查询推荐的核心思想其实就是，对于用户的输入，查找相似的关键词并进行返回。而测量拉丁文的文本相似度，最常用的指标是编辑距离（Edit Distance）。

由一个字符串转成另一个字符串所需的最少编辑操作次数，我们就叫作编辑距离。

编辑距离越小，说明这两个字符串越相似，可以互相作为查询推荐。编辑操作有这三种：

• 把一个字符替换成另一个字符；
• 插入一个字符；
• 删除一个字符。

比如，我们想把 mouuse 转换成 mouse，有很多方法可以实现，但是很显然，直接删除一个“u”是最简单的，所以这两者的编辑距离就是 1。

状态转移

编辑距离只需要求最小的操作次数，并不要求列出所有的可能。而且排列过程非常容易出错，还会浪费大量计算资源。

先考虑最简单的情况。假设字符串 A 和 B 都是空字符串，那么很明显这个时候编辑距离就是 0。如果 A 增加一个字符 a1，B 保持不动，编辑距离就增加 1。同样，如果 B 增加一个字符 b1，A 保持不动，编辑距离增加 1。但是，如果 A 和 B 有一个字符，那么问题就有点复杂了，我们可以细分为以下几种情况。

插入字符的情况。A 字符串是 a1 的时候，B 空串增加一个字符变为 b1；或者 B 字符串为 b1 的时候，A 空串增加一个字符变为 a1。很明显，这种情况下，编辑距离都要增加 1。

替换字符的情况。当 A 和 B 都是空串的时候，同时增加一个字符。如果要加入的字符 a1 和 b1 不相等，表示 A 和 B 之间转化的时候需要替换字符，那么编辑距离就是加 1；如果 a1 和 b1 相等，无需替换，那么编辑距离不变。

我们在每一个子问题中，都只需要保留一个最优解。之后的问题求解，只依赖这个最优值。这种求编辑距离的方法就是动态规划，而这些子问题在动态规划中被称为不同的状态。

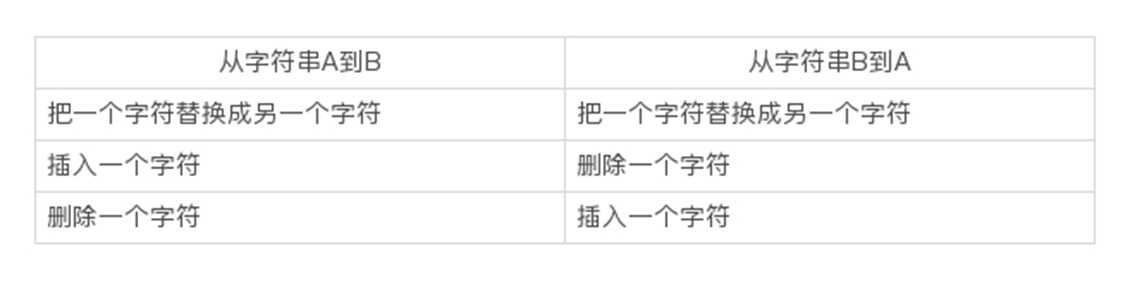
字符串 A 演变到 B 的每一种变化方式，都可以找到对应的从字符串 B 演变到 A 的某种方式，两者的操作次数一样。自然，代表最小操作次数的编辑距离也就一样了。

总结

学数学固然是为了得到结果，但是学习的过程，是要学会解决问题的方法和思路。

能够使用动态规划解决的问题，通常只关心一个最优解，而这个最优解是单调改变的，例如最大值、最小值等等。因此，动态规划中的每种状态，通常只保留一个当前的最优解，这也是动态规划效率比较高的原因。