查找算法-二分查找

Posted 2021-02-28 stringarray

二分查找的引入

在介绍二分查找之前，对于基于数字索引的数组元素的查找，我们可能第一反应都是遍历这个数组，直到给定数组元素值和待查找的值相等时，返回索引值并退出，否则一直遍历到最后一个元素，如果还是没有找到则返回 -1，这样的查找虽然是简单粗暴了点，但是对于规模不大的数据集，也是没什么问题的，不过很明显，对于 n 个元素的数组，这种查找的时间复杂度是 O(n)，随着数据规模的增加，性能会越来越差，设想如果数据集的长度是 40 亿（约 2 的 32 次方），那么最差的情况需要遍历数组 40 亿次，简直不敢想象需要花费多长时间！那有没有性能搞好的算法来解决这个问题呢？

在进一步探讨这个问题之前，我们先来看一个生活中的例子。我们日常生活中，很多人应该有这种经历，朋友、同学或者同事淘了个宝贝，神秘兮兮的过来让大家猜多少钱，在约定一个价格范围之后（比如 10-100），大家会七嘴八舌的猜起价格来：

同事A：新淘了个宝贝，猜猜多少钱？
同事B：50块。
同事A：高了。
同事C：30块。
同事A：低了。
同事D：40块。
同事A：高了。
同事E：36块。
同事A：对了。

如果我们用顺序遍历的逻辑，最差需要 91 次，才能猜到价格，现实生活中，没人会这么干，我们采用上面这种逻辑，只需要 4 次就猜到价格了，快了几十倍，而且数据量越大，优势越明显。基于这种思路，我们的算法科学家提炼出了二分查找算法，帮助我们在给定数据集中快速定位要查找的元素。

实现原理

所谓二分查找，针对的是一个有序的数据集合（这点很重要），查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。注意到二分查找针对的必须是已经排序过的有序数组，否则不能使用该算法。图示如下：

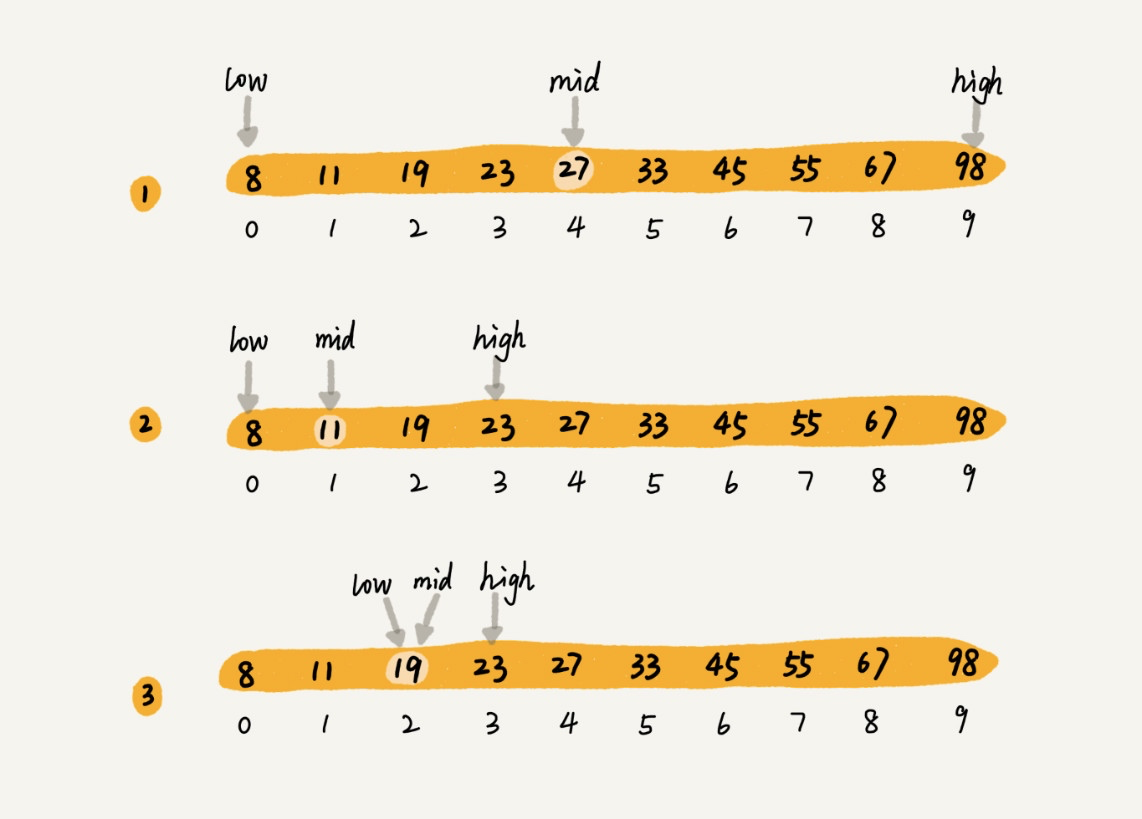
示例代码

思路比较简单，我们将其通过 php 代码实现如下：

<?php
    // 递归版
    function binary_search($nums, $num)
    {
        return binary_search_internal($nums, $num, 0, count($nums) - 1);
    }
    
    function binary_search_internal($nums, $num, $low, $high)
    {
        if ($low > $high) {
            return -1;
        }
    
        $mid = floor(($low + $high) / 2);
        if ($num > $nums[$mid]) {
            return binary_search_internal($nums, $num, $mid + 1, $high);
        } elseif ($num < $nums[$mid]) {
            return binary_search_internal($nums, $num, $low, $mid - 1);
        } else {
            return $mid;
        }
    }
    
    $nums = [1, 2, 3, 4, 5, 6];
    $index = binary_search($nums, 5);
    print $index;
	
    // 非递归版
    function BinaryQuery(array $container, $search)
    {
        $top = count($container);
        $low = 0;
        while ($low <= $top) {
            $mid = intval(floor(($low + $top) / 2));
            if (!isset($container[$mid])) {
                return ‘没找着哦‘;
            }
            if ($container[$mid] == $search) {
                return $mid;
            }
            $container[$mid] < $search && $low = $mid + 1;
            $container[$mid] > $search && $top = $mid - 1;
        }
    }

性能分析

二分查找的时间复杂度是 O(logn)。这是一个非常恐怖的数量级，有时候甚至比 O(1) 还要高效，比如我们要在开头提到的 40 亿个数字中查找某一个元素，也只需要32次（2 的 32 次方是 40 亿数量级），这真的是非常高效了，正因如此二分查找在线性表结构中的应用非常广泛。

但是使用二分查找需要注意一个前提，那就是针对有序数组，换言之，二分查找适用于变动不是很频繁的静态序列集，如果序列集变动很频繁，经常进行插入删除操作，那么就要不断维护这个序列集的排序，这个成本也很高，因此，这种情况下就不适用二分查找了，比如我们的数据库查询，增删改查很频繁，显然不是通过二分查找来进行查询的，后面我们会讨论，如何针对动态变化的序列集进行查询操作。

二分查找的变形: 从给定序列中查找第一个或最后一个匹配元素

符合标准的二分查找条件的序列一般是比较理想的情况，如果要查找的元素在序列中有多个怎么办？所以我们要给大家介绍的第一个常见的变形版本，就是在一个给定排序序列中查找第一个等于给定值的元素。在继续往下看之前，你不妨借机先思考一下要怎么实现。

其实关键节点就在于在序列中找到值等于待查找元素值时的处理。如果此时 $mid 位置已经到了序列的最左边，不能再往左了，或者序列中索引小于 $mid 的上一个元素值不等于待查找元素值，那么此时 $mid 就是第一个等于待查找元素值的位置；否则还要继续往前找。

对应的 PHP 实现代码如下，其他地方都一样，就是 $num == $nums[$mid] 时的处理逻辑变了：

<?php
    
    /**
     * 二分查找变形版：查找第一个值等于给定值的元素（数组中包含重复数据）
     */
    function binary_search($nums, $num)
    {
        if (count($nums) <= 1) {
            return 0;
        }
        return binary_search_internal($nums, $num, 0, count($nums) - 1);
    }

	function binary_search_internal($nums, $num, $low, $high)
    {
        if ($low > $high) {
            return -1;
        }
    
        $mid = floor(($low + $high) / 2);
        if ($num < $nums[$mid]) {
            return binary_search_internal($nums, $num, $low, $mid - 1);
        } elseif ($num > $nums[$mid]) {
            return binary_search_internal($nums, $num, $mid + 1, $high);
        } else {
            if ($mid == 0 || $nums[$mid-1] != $num) {
                return $mid;
            } else {
                return binary_search_internal($nums, $num, $low, $mid - 1);
            }
        }
    }
    
    $nums = [1, 2, 3, 3, 4, 5, 6];
    $index = binary_search($nums, 3);
    print $index;

既然有第一个等于给定值的查询，自然就有最后一个等于给定值的查询，这就是二分查找的第二个变形版本：在给定已排序序列中查找最后一个等于给定值的元素。实现逻辑和上面类似，只需要改动 $num == $nums[$mid] 时的处理逻辑，只是这时的条件变成了 $mid 位置到了序列的最右边，不能再往后了，或者索引大于 $mid 的后一个元素值不等于带查找元素，才返回 $mid，否则，还要继续往后找。在我给出实现代码之前，你能自行实现这段代码吗？不防动手写一下，或者头脑中构思下。

下面我来给出查找最后一个等于给定值的元素的 PHP 实现代码，由于其他部分都一样，我只给出 binary_search_internal 函数的代码：

function binary_search_internal($nums, $num, $low, $high)
    {
        if ($low > $high) {
            return -1;
        }
    
        $mid = floor(($low + $high) / 2);
        if ($num < $nums[$mid]) {
            return binary_search_internal($nums, $num, $low, $mid - 1);
        } elseif ($num > $nums[$mid]) {
            return binary_search_internal($nums, $num, $mid + 1, $high);
        } else {
            if ($mid == count($nums) - 1 || $nums[$mid + 1] != $num) {
                return $mid;
            } else {
                return binary_search_internal($nums, $num, $mid + 1, $high);
            }
        }
    }

二分查找的变形: 在给定序列中查找第一个大于等于或最后一个小于等于给定值的元素

我们之前的需求都是查找等于给定值，现在变成了大于等于给定值，所以我们要在 $nums[$mid] >= $num 这个判断条件上做文章，思路还是和之前两个变形版本类似，当 $mid 已经是最左边的元素，或者 $mid 的前一个元素值小于给定查询值，则 $mid 对应元素即为满足条件的元素，否则继续往前查找。对应的 PHP 实现代码如下：

<?php
    
    /**
     * 二分查找变形版：查找第一个大于等于给定值的元素（数组中包含重复数据）
     */
    function binary_search($nums, $num)
    {
        if (count($nums) <= 1) {
            return 0;
        }
        return binary_search_internal($nums, $num, 0, count($nums) - 1);
    }
    
    function binary_search_internal($nums, $num, $low, $high)
    {
        if ($low > $high) {
            return -1;
        }
    
        $mid = floor(($low + $high) / 2);
        if ($num <= $nums[$mid]) {
            if ($mid == 0 || $nums[$mid - 1] < $num) {
                return $mid;
            } else {
                return binary_search_internal($nums, $num, $low, $mid - 1);
            }
        } elseif ($num > $nums[$mid]) {
            return binary_search_internal($nums, $num, $mid + 1, $high);
        }
    }
    
    $nums = [1, 2, 3, 3, 4, 5, 6];
    $index = binary_search($nums, 3);
    print $index;

同样，与之相对的，还有我们这次分享中最后要讨论的一个二分查找的变形版本：在给定序列中查找最后一个小于等于给定值的元素。

有了前面几个变形版本的铺垫，相信你自己就可以写出对应的实现代码了。这次的判断节点变成了 $nums[$mid] <= $num，其中 $num 是待查找的元素值，当 $mid 已经是最后一个元素索引，或者 $mid 的后一个元素值大于 $num 则当前 $mid 对应元素就是要查找的元素，否则要继续往后查找。

对应的 PHP 实现代码如下：

<?php
    
    /**
     * 二分查找变形版：查找最后一个小于等于给定值的元素（数组中包含重复数据）
     */
    function binary_search($nums, $num)
    {
        if (count($nums) <= 1) {
            return 0;
        }
        return binary_search_internal($nums, $num, 0, count($nums) - 1);
    }
    
    function binary_search_internal($nums, $num, $low, $high)
    {
        if ($low > $high) {
            return -1;
        }
    
        $mid = floor(($low + $high) / 2);
        if ($num >= $nums[$mid]) {
            if ($mid == count($nums) - 1 || $nums[$mid + 1] > $num) {
                return $mid;
            } else {
                return binary_search_internal($nums, $num, $mid + 1, $high);
            }
        } elseif ($num < $nums[$mid]) {
            return binary_search_internal($nums, $num, $low, $mid - 1);
        }
    }
    
    $nums = [1, 2, 3, 3, 4, 5, 6];
    $index = binary_search($nums, 3);
    print $index;

二分查找案例：IP 地址对应城市查询

今天我们来分享一个二分查找的实际使用案例 —— 根据用户的 IP 地址，获取用户所在的城市。

我们知道每个城市都有对应的 IP 地址段，这个在网上搜一下就能拿到。然后我们可以将这些不同城市 IP 地址段起始值转化为整型数字（转化函数Google/百度搜下就能找到），进而对其进行排序，就可以得到一个有序的序列。比如杭州和北京，IP区间分别是 [183.128.0.0,183.159.255.255] 和 [110.96.0.0,110.127.255.255]，转化为数字后对应区间分别是 [3078619136,3080716287] 和 [1851785216,1853882367]，这样，就可以对这两个区间起始值排序为 [1851785216,3078619136]。

此外我们还需要存储每个区间值对应的城市，以便找到对应位置后可以快速定位对应城市，我们可以把这个映射关系存储到数据库里面，存储字段包括城市、起始 IP、结束 IP，这里有一个前提是不同城市区间值不可能交叉，否则没法玩。

接下来就是二分查找排上用场的时候了，我们将待查找 IP 转化为数字，然后在排序序列中查找最后一个起始 IP 小于等于待查找 IP 的位置，通过该起始 IP 在数据库中定位到对应记录，判断待查找 IP 是否在这个 IP 区间范围内，如果在的话则返回对应城市，不在的话，就返回没找到。

如果你在面试的时候遇到这个问题，也就可以从容作答了。