leetcode查找算法(顺序查找,二分法,斐波那契查找,插值查找,分块查找)
Posted 是安澜啊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode查找算法(顺序查找,二分法,斐波那契查找,插值查找,分块查找)相关的知识,希望对你有一定的参考价值。
目录
查找算法也可以叫搜索算法。就是从一个有序数列中找出一个特定的数,常用于判断某个数是否在数列中,或者某个数在数列中的位置。在计算机应用中,查找是常用的基本运算,是算法的重要组成部分。
查找数列按照操作方式可以分成静态查找和动态查找。静态查找只在数列中查找特定的数字,不对数列做任何修改(可以进行排序)。因此静态查找时除了可以返回特定数是否存在,还可以返回这个特定数在当前数列中的序列号(下标)。动态查找在查找的同时进行插入或删除操作。因此,动态查找只能返回特定数是否存在当前数列中。
1.顺序查找
原理
顺序查找是最简单、最直接的查找算法。顺序查找就是将数列从头到尾按照顺序查找一遍,是最没技术含量、最容易理解的算法。
顺序查找属于静态查找。因为顺序查找是按照从头到尾的方法查找特定数的,所以也可以不对数列进行排序,直接开始查找。为了样式的统一,这里还是采用了有序的数列。以iList数列为例,顺序查找最坏的情况需要查找len(iList)次才能找到目标或者确认数列中没有目标。
第一次查找
从iList数列的首个数字(iList[0])开始,比较查找的数字是否相等。如果相等,就返回数字的下标并退出,否则比较数列中的下一个数字,

第N次查找

经过第 N 次的查找,终于在数列中找到了与key相等的元素,返回这个元素的下标(在实际使用中数列中有0个、1个、1个以上的元素与key相等都是有可能的。在这里排除了多个元素符合条件的情况)。
代码
生成随机数列表我们使用一个函数,之后导入进去使用。
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:20211210
# author:yang
import random
def randomList(n):
"""返回一个长度为n的整数列表,数据范围为[0,1000)"""
iList = []
for i in range(n):
iList.append(random.randrange(1000))
return iList
if __name__=="__main__":
iList = randomList(10)
print("iList:",iList)#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from randomList import randomList
import timeit
def sequentialSearch(iList,key):
iLen = len(iList)
for i in range(iLen):
if iList[i] == key:
return i
return -1
if __name__ == "__main__":
iList = randomList(10)
print("iList:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = sequentialSearch(iList,key)
if res >= 0:
print("%d is in the list,index is:%d\\n"%(key,res))
else:
print("%d is not in the list\\n"%key)
结果

拓展
1. random.choice()
定义:choice() 方法返回一个列表,元组或字符串的随机项。
语法:random.choice( seq )
- seq -- 可以是一个列表,元组或字符串。
2. random.randrange()
定义:randrange() 方法返回指定递增基数集合中的一个随机数,基数默认值为1。
语法:random.randrange ([start,] stop [,step])
- start -- 指定范围内的开始值,包含在范围内。
- stop -- 指定范围内的结束值,不包含在范围内。
- step -- 指定递增基数。
总结:这个方法很基础很基础,效率太慢了。
2.二分法
原理
在一个有序数列中查找一个特定的数字,用顺序查找无疑是最没效率方法了。直接找数列中间的那个数字与被查找数(key)相比较。如果这个数字比被查找数(key)小,无疑被查找数一定是在这个有序数列的后半部分;否则被查找数一定是在这个有序数列的前半部分。下面还是以iList数列(数字0~9)为例,假设被查找数key为9。
第一次查找
iList的长度为len(iList)=10,最中间的元素下标就是数列首元素的下标(0)和数列尾元素的下标(9)的和除以2,(0+9)//2=4。iList[mid]就是iList[4],第一次比较就是和iList[4]比较,如图
所示。
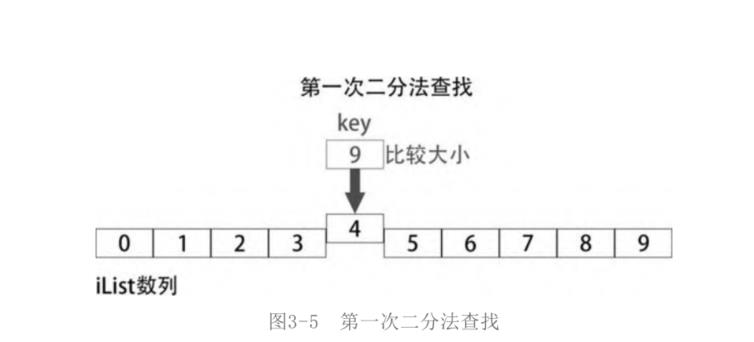
显然key要比iList[4]大,所以key必定是在iList[4]的后半部分。
第二次查找
后半部分的中间元素下标是(5+10)//2=7,所以iList[mid]是iList[7]。第二次比较是key和iList[7]比较,如图所示。
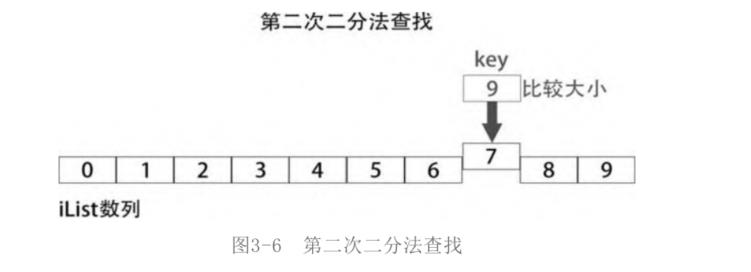
key比iList[7]要大,Key必定在iList[7]后半部分。后半部分中间元素下标是(8+9)//2=8,此时只剩下两个元素了,再使用二分法查找就得不偿失了。直接比较数的大小就好了。
代码
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from randomList import randomList
import sort
def binarySearch(iList,key):
iLen = len(iList)
left = 0
right = iLen - 1
while right - left > 1:
mid = (left + right)// 2
if key < iList[mid]:
right = mid
elif key > iList[mid]:
left = mid
else:
return mid
if key == iList[left]:
return left
if key == iList[right]:
return right
else:
return -1
if __name__ == "__main__":
iList = sort.quickSort(randomList(10))
print("iList2:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = binarySearch(iList,key)
if res >= 0:
print("%d is in the list,index is %d.\\n"%(key,res))
else:
print("%d is not in the list.\\n"%key)
结果

注:sort.py(快速排序算法)
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:20211210
# author:yang
from randomList import randomList
import timeit
def quickSort(iList):
if len(iList) <= 1:
return iList
left = []
right = []
for i in iList[1:]:
if i <= iList[0]:
left.append(i)
else:
right.append(i)
return quickSort(left) + [iList[0]] + quickSort(right)
if __name__ == "__main__":
iList = randomList(10)
print(iList)
print(quickSort(iList))
# print(timeit.timeit("selectionSort(iList)","from __main__ import selectionSort,iList",number = 1))
总结:同样是查找数字9,顺序查找需要到第10次才能找到(这是顺序查找最不顺利的情况),而二分法查找只需要3次(这也是最不顺利的情况),明显二分法查找要比顺序查找的效率高。
记住:要是排好序的数列才可以。
3.斐波那契查找
斐波那契数列(Fibonacci)又称黄金分割数列,指的是这样一个数列:1,1,2,3,5,8,13,21,····。在数学上,斐波那契被递归方法如下定义: F (1)=1, F (2)=1, F ( n )= F ( n -1)+ F ( n-2) ( n ≥2)。该数列越往后,相邻的两个数的比值越趋向于黄金比例值(0.618)。斐波那契查找就是在二分法查找的基础上根据斐波那契数列进行分割的。
原理
Fibonacci查找与二分法查找几乎一样,只是在选取比较点(参照点)的位置有所区别。二分法选的是将数列中间的那个元素作为比较点(参照点),而Fibonacci查找则选取了数列中中间略微靠后点的位置作为比较点,也就是黄金分割点。假设被查找数列的长度为1,那么Fibonacci查找选取的比较点则在0.618的位置。这是由Fibonacci数列的特性决定的。
既然叫作Fibonacci查找,首先列出一个Fibonacci数列。[1, 2,3, 5, 8, 13, 21],这个Fibonacci数列只是提供了被查找数列中参数点的位置,基本上就是下标。以iList = [0, 1, 2, 3, 4, 5, 6, 7,8, 9]为例,共有len(iList)=10个元素。选择一个比len(iList)稍大的Fibonacci数,也就是13。比13小一号的Fibonacci数就是8,那么首次选取的参照点就是iList中的iList[8]。如果被寻找数key比iList[8]小,就看一下比8小一号的Fibonacci数(5),第二次选取的参照点就是iList[5]。以此类推,就是把Fibonacci数当作被查找数列的位置参数来使用。
以iList为被查找数列、key=7为例开始查找。
第一次查找
iList长度为10,Fibonacci数列中没有10,因此假设iList的长度为 13 ( 13 是 Fibonacci 数 ) 。 比 13 小 的 Fibonacci 数 是 8 , 按 照Fibonacci查找的原理,实际上参照点应该是iList的第8个数字,也就是iList[7]。为了直观,这里选取的是iList[8],这样也是可以的。

因为key比参照点iList[8]要小,说明被寻找的数在iList的前面部分。
第二次查找
第二次查找是在iList[0:8]之间查找,这次被查找数列的长度是8,比8小一号的Fibonacci数是5,那么这次的参照点就是iList[5]。
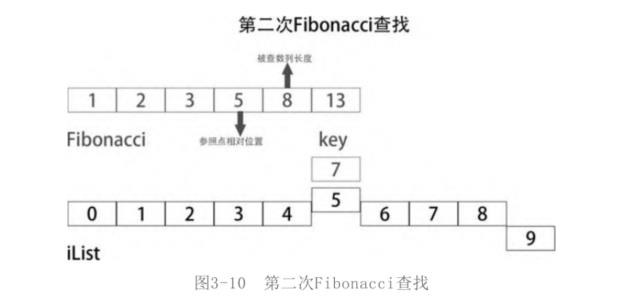
此时key要比iList[5]大,说明被寻找的数在iList[0:8]的后半部分。也就是在iList[6,8]之间。
第三次查找
按照正常流程剩下有“嫌疑”的数只剩下iList[6]和iList[7]了,已经无须用Fibonacci查找了,这里还是按照Fibonacci的方案找一次。iList[6,8]之间只有2个数了,但是Fibonacci查找时却是在iList[6]、iList[7]、iList[8]这3个数组成的数列中查找的。因此被查找数列的长度实际是3,那么参照点应该是比3稍小一号的Fibonacci数2。也就是这个被查找数列中的第2个数iList[7]。

Fibonacci查找作为二分法查找的变种,在一般情况下效率肯定要比顺序查找高,与二分法不相上下。根据数据在数列中的分布状态,二分法和Fibonacci法很难说哪个更快一些(比如被查找的数正好在数列的前端,Fibonacci查找效率还不如二分法查找)。
代码
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from types import MemberDescriptorType
from warnings import resetwarnings
from randomList import randomList
import sort
def fibonacci(n):
"""返回fibonacci数列的最后一个元素"""
fList = [1,1]
while n > 1:
fList.append(fList[-1]+fList[-2])
n -= 1
return fList[-1]
def fibonacciSearch(iList,key):
iLen = len(iList)
left = 0
right = iLen - 1
indexSum = 0
k = 1
while fibonacci(k) -1 < iLen -1:
k += 1
while right - left > 1:
mid = left + fibonacci(k-1)
if key < iList[mid]:
right = mid - 1
k -= 1
elif key == iList[mid]:
return mid
else:
left = mid + 1
k -= 2
if key == iList[left]:
return left
elif key == iList[right]:
return right
else:
return -1
if __name__ == "__main__":
iList = sort.quickSort(randomList(10))
print("iList:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = fibonacciSearch(iList,key)
if res >= 0:
print("%d is in the list,index is %d.\\n"%(key,res))
else:
print("%d is not in the list.\\n"%key)
在fibonacciSearch.py中使用自定义的fibonacci函数通过变量 k返回一个fibonacci数fibonacci(k)。返回的这个fibonacci(k)可以看成被搜索数列的长度。而fibonacci(k-1)则是被搜索数列中参照点“相对位置”。在fibonacciSearch.py的第36行声明的mid = left +fibonacci(k-1)则是参照点在iList数列中的“绝对位置”,可以视为列表下标。
4.插值查找
在被查找数列中选取比较点(参照点)时,二分法采用的是中点,Fibonacci法采用的是黄金分割点。二分查找法是最直观的,Fibonacci查找法可能是最“美观”的,但都不是最科学的。那么,如
何选取最科学的那个比较点(参照点)呢?通常情况下被查找数列都不是等差的,也不知道数列的差值分布状态,没法确定到底选择哪个点是“最优解”。插值算法则给出了一个大多数情况下的理论上最科学的比较点(参照点)。
原理
以英语词典为例,如果是要找以a开头的单词。一般都不会从中间位置开始翻(二分查找法),也不会从黄金分割点(页数×0.618)的位置开始找(Fibonacci查找法)。直觉上就是应该从字典的前面开始查找。但数学没有直觉,它会告诉我们mid = left + (key -iList[left]) *(right - left) // (iList[right] -iList[left]),不管是找哪个字母开头的单词,还是在任意数列中寻找任意数,这个点在大多数情况下就是最优的比较点。
第一次查找
以iList为被查找数列、key=7为例开始查找。当前iList = range(0,10) = [0, 1, 2, 3, 4, 5, 6, 7, 8,9],是一个差值为1的等差数列。在插值查找给出的公式中mid为比较点(参照点),left为被查找数列列首的下标, right为被查找数列列尾的下标,如图。

第一次查找就找到了被查找数。在搜索等差数列时,插值查找可能是最快的算法。
第二次查找
再来看看等比数列的查找,重新设定iList = [pow(2, i) for i in range(0, 10)],即iList = [1, 2, 4, 8, 16, 32, 64, 128,256, 512]。当前iList为一个比值为2的等比数列,设置key = 128,开始在iList中查找,如图。

第一次查找并没有找到目标,重新在数列iList[mid, right]中查找,也就是将left右移到当前mid的位置,然后重新计算mid,确定比较点(参照点),如图
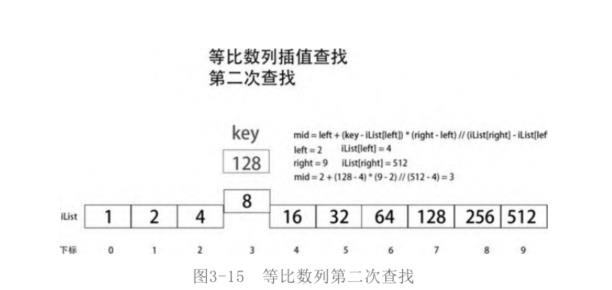
第二次仍然没有找到目标,将left右移到当前mid的位置,继续下一次的查找。这次mid= 3 + (128 – 8) * ( 9 – 3) // (512 – 8)= 4。每次mid只向右移动一个元素,按照这个速度来看,效率远不如二分法查找和Fibonacci查找。
代码
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from types import MemberDescriptorType
from warnings import resetwarnings
from randomList import randomList
import sort
def insertSearch(iList,key):
iLen = len(iList)
left = 0
right = iLen - 1
while right - left > 1:
mid = left + (key - iList[left]) * (right - left) // (iList[right] - iList[left])
if mid == left:
mid += 1
if key < iList[mid]:
right = mid
elif key > iList[mid]:
left = mid
else:
return mid
if key == iList[left]:
return left
elif key == iList[right]:
return right
else:
return -1
if __name__ == "__main__":
iList = sort.quickSort(randomList(10))
print("iList:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = insertSearch(iList,key)
if res >= 0:
print("%d is in the list,index is %d.\\n"%(key,res))
else:
print("%d is not in the list.\\n"%key)
当iList数列元素分布比较大时,mid这个比较点可能会一直都等于left而造成死循环。因此在insertSearch.py的第24、25行需要加上一个限制条件。
总结:
插值查找法也是二分查找法的进阶算法,当数列中的元素分布得比较广的情况下插入查找的效果并不太好。等差数列用最好。
5.分块查找
分块查找和以上几种查找方式有所不同:顺序查找的数列是可以无序的;二分法查找和斐波那契查找的数列必须是有序的;分块查找介于两者之间,需要块有序,元素可以无序。
原理
分块查找首先按照一定的取值范围将数列分成数块。块内的元素是可以无序的,但块必须是有序的。什么叫块有序呢?意思是处于后面位置的块中的最小元素都要比前面位置块中的最大元素大。
重新设置一个iList = [9, 17, 13, 5, 2, 26, 7, 23, 29]。当前这个数列iList是无序的,设置被查找数key=26。按照分块查找的步骤,首先要做的是将iList分为数块,至少要分成2块,否则就和顺序
查找没区别了。观察iList数列,发现这个数列最大的数都不超过30,所以这里按照0~9, 10~19, 20~29这3个区间将iList分为3块(并不是必须这样分,也可以分成2块、4块、5块……选择一个比较方便的值分块就可以)

分完块后,块与块之间有序。block2中的最小元素13比block1中的最大元素9大。block3中的最小元素23比block2中的最大元素17大。block1、block2、block3中块内的元素无序。分完块后开始查找。
第一次查找
第一次查找是将被查找数key与块的分界数相比较(也可以与每个块中最大的那个元素比较),确定被查找数key属于哪个块,如图。

被查找数key比block2的分界数19大,因此只能在block3中查找了。
第二次查找
块内的查找就是逐个对比,也就是顺序查找了。

代码
#!/user/bin/env/python3
#-*-conding:utf-8 -*-
# data:202112112
# author:yang
import random
from randomList import randomList
import sort
def divideBlock():
global iList,indexList
sortList = []
for key in indexList:
subList = [i for i in iList if i < key[0]]
key[1] = len(subList)
sortList += subList
iList = list(set(iList) - set(subList))
iList = sortList
print()
return indexList
def blockSearch(iList,key,indexList):
print("iList = %s" %str(iList))
print("indexList = %s" %str(indexList))
print("Find The number : %d" %key)
left = 0
right = 0
for indexInfo in indexList:
left += right
right += indexInfo[1]
if key < indexInfo[0]:
break
for i in range(left,right):
if key == iList[i]:
return i
return -1
if __name__ == "__main__":
indexList = [[250,0],[500,0],[750,0],[1000,0]]
iList = sort.quickSort(randomList(20))
print("iList1:",iList)
divideBlock()
print("iList2:",iList)
keys = [random.choice(iList),random.randrange(min(iList),max(iList))]
for key in keys:
res = blockSearch(iList,key,indexList)
if res >= 0:
print("%d is in the list,index is %d.\\n"%(key,res))
else:
print("%d is not in the list.\\n"%key)结果
 总结
总结
分块查找可以看成顺序查找的进阶算法。虽然在分块时会耗费点时间,但是在后期的查找会快很多。一般情况下分块查找比顺序查找要快。
参考
图解leetcode初级算法(python版)--胡松涛
以上是关于leetcode查找算法(顺序查找,二分法,斐波那契查找,插值查找,分块查找)的主要内容,如果未能解决你的问题,请参考以下文章