静态查找算法 - 顺序查找二分查找插值查找斐波那契查找
Posted 数据结构与算法
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了静态查找算法 - 顺序查找二分查找插值查找斐波那契查找相关的知识，希望对你有一定的参考价值。
作者丨STzen
https://www.jianshu.com/p/f371ba694043
查找概念
查找(Searching)： 即根据给定的某个值，在查找表中确定一个其关键字给定值的数据元素(或记录)。
查找表(Search Table)：有同一类型的数据元素(或记录)构成的集合。
关键字(Key)： 数据元素中某个数据项的值，又称键值，可用于标识一个数据元素。
主关键字(Primary Key)： 可以唯一标识一个记录的关键字。
次关键字(Secondary Key): 可以识别多个数据元素(或记录)的关键字。
查找表分类
静态查找(Static Search Table)：只作查找操作的查找表。主要操作有：
查询某个“特定的”数据元素是否在查找表中。
检索某个“特定的”数据元素和各种属性。
动态查找表(Dynamic Search Table)：在查找过程中同时插入查找表中不存在的数据元素，或者从查找表中删除已经存在的某个特定的数据元素。主要操作有两个：
查找时插入数据元素；
查找时删除数据元素。
一、顺序查找
顺序查找(Sequential Search)又叫线性查找，是最基本查找技术，它的查找过程是：从表中第一个(或最后一个)记录开始，逐个进行记录关键字和给定值比较，若相等，则查找成功，返回查找记录；若知道最后一个记录都不相等，则表中没有所查的记录，查找不成功。
顺序查找代码实现
/**
* 1.顺序查找
* a是要查找的数组
* n是查找的数组个数， key为查找的关键字
*/
int sequence_search(int *a, int n, int key){
for (int i = 1; i < n; i++) {
if (a[i] == key)
return i;
}
return 0; // 返回0表示没找到
}
顺序查找优化
因为上一段代码每次循环时都需要对i是否越界进行判断，实际上可以省去这一步，就是添加一个哨兵来解决。
在查找方向的尽头(查找表第一个元素或者最后一个元素)放置“哨兵”，免去查找过程越界的判断。
顺序查找优化代码实现(添加哨兵)
/**
* 1.1顺序查找优化，添加哨兵
* 注意 这里将a[0]设置为哨兵 那么a[0]就不能用来存储需要查找的数据
* 如果找到 返回的数据表示在数组中索引所在的位置 从0开始的 也就是说如果返回的是1的话 是数组的第二个元素 所以可以在返回的结果上+1
* 同样 这儿哨兵也可以放在数组的尾巴上 a[n-1] = key
*/
int guard_search(int *a, int n, int key){
int i = n;
a[0] = key; // 哨兵
while (a[i] != key)
i--;
return i; // 返回0表示没找到
}代码解释
代码从尾部开始查找。
由于a[0] = key，那么在a[i] = key时，返回i值，查找成功。否者一定在最终的a[0]处等于key，此时返回的是0，查找失败。
这里将a[0]设置为哨兵 那么a[0]就不能用来存储需要查找的数据。
哨兵也可以放在数组的尾巴上 a[n-1] = key,那么这里也不能用来存放数据查找数据。
顺序查找总结
顺序查找平均查找次数为(n+1)/2。
顺序查找的时间复杂度为O(n).
查找效率低下，在一些小型数据查找时适用。
二、折半查找(二分查找)
折半查找前提：线性表中的记录必须是关键码有序(通常从小到大有序)，线性表必须采用顺序存储。
折半查找的基本思想：
在有序表中，取中间记录作为比较对象，若给定值 = 中间记录的关键字，则查找成功。
给定值 < 中间记录关键字，则在中间记录左半区域继续查找；
给定值 > 中间记录关键字，则在中间记录右半区域继续查找；
不断重复上述过程，直到查找成功，若所有查找区域无记录，查找失败为止。
折半查找(二分查找)代码实现
/**
* 2.二分查找
*/
int Binary_Search(int * a, int n, int key){
int low,mid,high;
low = 1;
high = n;
while (low <= high) {
mid = (low + high) / 2;
if (a[mid] < key)
low = mid + 1;
else if(a[mid] > key)
high = mid - 1;
else
return mid;
}
return 0; // 找不到 返回0
}
折半查找总结
折半查找的时间复杂度为O(logn)。明显优于顺序查找。
折半查找的前提条件需要有序的顺序存储，对于静态查找表比较合适。
三、插值查找
对于插值查找，就是对于二分查找的优化，将二分查找中的mid = (low + high) / 2改为mid = low + (high - low) * (key - a[low]) / (a[high] - a[low])。
插值查找是根据查找关键子key与查找表中最大最小记录关键字比较后的查找方法，核心在于插值计算公式(key-a[low])/(a[high] - a[low])。
插值查找代码实现
/**
* 3.插值查找
*/
int Insert_Search(int * a, int n, int key){
int low,mid,high;
low = 1;
high = n;
while (low < high) {
mid = low + (high - low) * (key - a[low]) / (a[high] - a[low]);
if (a[mid] < key)
low = mid + 1;
else if(a[mid] > key)
high = mid - 1;
else
return mid;
}
return 0; // 没找到 返回0
}
插值查找总结
时间复杂度依旧为O(logn)。
对于表长较大，而关键字分部比较均匀的查找表来说，平均性能要比折半好很多。
如果数组中的分部类似{1，100，200，1000，10000...10000}这种极端不均匀的数据，用插值法也不太合适。
四、菲波那切查找
菲波那切查找是利用黄金分割原理来实现的。
菲波那切查找用到了菲波那切数列，关于在这里有提到过递归和分治思想之递归
斐波那契查找首先要利用斐波那契数列数组来进行黄金分割。
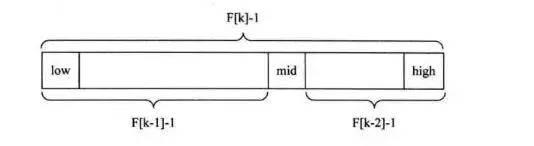
菲波那切查找代码
int F[100]; //斐波那契数列
/**
* 4.斐波那契查找
*/
int Fibonacci_Search(int *a, int n, int key){
int low, mid, high, i, k = 0;
low = 1;
high = n;
while (n > F[k] - 1)
k++;
for (i = n; i < F[k] - 1; i++)
a[i] = a[n];
while (low <= high) {
mid = low + F[k-1]-1;
if (key < a[mid]) {
high = mid - 1;
k = k - 1;
}else if (key > a[mid]){
low = mid + 1;
k = k - 2;
}else{
if (mid <= n)
return mid; // 若相等则说明mid即为查找到的位置
else
return n;
}
}
return 0;
}
测试
int main(int argc, const char * argv[]) {
int arr[] = {1000,2,3,4,5,6,7,8,9,10};
int key = 2; // 要查找的值
int reslut = sequence_search(arr, 10, key);
printf("1. 顺序查找
reslut = %d
", reslut);
int reslut2 = guard_search(arr, 9, key);
printf("
1.1 顺序查找（哨兵模式)
reslut2 = %d
", reslut2);
int result3 = Binary_Search(arr, 10, key);
printf("
2. 折半查找
reslut3 = %d
", result3);
int result4 = Insert_Search(arr, 10, key);
printf("
2.1 插入查找
reslut4 = %d
", result4);
F[0] = 0;
F[1] = 1;
for (int i = 2; i < 100; i++)
F[i] = F[i-1] + F[i-2];
int result5 = Fibonacci_Search(arr, 10, key);
printf("
3. 斐波那契查找
reslut5 = %d
", result5);
return 0;
}
推荐↓↓↓
长
按
关
注
以上是关于静态查找算法 - 顺序查找二分查找插值查找斐波那契查找的主要内容，如果未能解决你的问题，请参考以下文章 学习数据结构笔记 ---查找算法(线性查找,二分查找,插值查找,斐波那契查找) [Algorithm]二分插值斐波那契查找算法 Java 代码实现