图论-拓扑排序

Posted 2021-02-21 sweetlittlebaby

学离散的偏序关系时的一个应用，

问题：小方准备组织一次演讲比赛，有如下环节（未排序）：

- 进行彩排

- 确定演讲主题

- 租借服装

- 确定比赛时间

- 确定比赛地点

- 确定参赛人员

- 申请经费

- 确定嘉宾人选

- 购买奖品，装饰物

- 比赛啦~

但是：

- 确定演讲主题之后才能确定比赛时间；

- 确定主题之后才能准备申请经费

- 在确定选手是否能参加之前先要确定比赛时间

- 购买何种装饰物需由比赛地点确定

- 只有当选手确定之后，才能去借服装，租场地和确定要邀请的嘉宾

- 如果申请经费没有成功，那么不能去购买奖品和装饰品

- 在彩排之前需要借服装和确定地点

- 比赛只有当嘉宾都邀请成功，已购买奖品而且彩排过才能进行

 

这些环节之间有一些约束关系，那么该怎么办呢;

画偏序关系的哈斯图形式（方案可能有多种）：

{

     偏序关系：（自反性，反对称性，传递性）

     哈斯图的画法：

      1，删除自环；

      2，具有传递性的，删掉可直达的

      3，重组位置，使得有向的箭头指向正上方或斜上方。

}

拓扑排序（topologicalSorting）：

输入：偏序集（A,R）

输出：A的元素在<意义下“从小到大”逐一列出所形成的序列

1，      B<- A,S<-R,List<-空

2，      while|B|>0 do

2.1,     从B中选择一个极小元x加入队列list

2.2，    B<- B- {x}

2.3，    S<- S|B

3，      return list

 

维基百科上关于Kahn算法的伪码描述：

 

L← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
    remove a node n from S
    insert n into L
    foreach node m with an edge e from nto m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S
if graph has edges then
    return error (graph has at least onecycle)
else 
    return L (a topologically sortedorder)

 

算法：（kahn）

对于一个有向无环图（DAG）来说：

1), 统计所有节点的入度，对于入度为0的节点就可以分离出来，然后将这个节点指向所有节点的入度减去1；

2), 重复1),知道所有的节点都被分离出来，拓扑排序结束。

3), 如果最后不存在入度为0的节点，那就说明图有环，无解。

注：对于入度为0的节点，则这个节点没有前驱，只要不是孤立节点，那么完成这个节点之后，对于它的所有后继节点来说，前驱结点就完成了一个，入度进行-1。

 

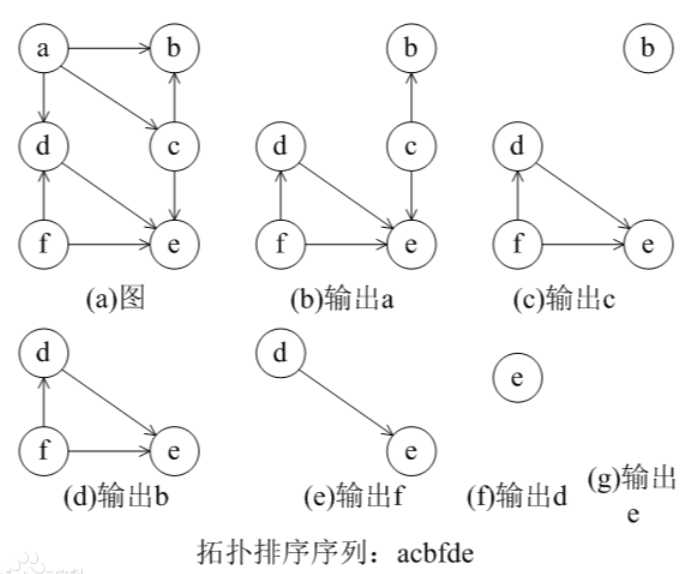
伪代码：（kahn）

bool toposort() {
    q = new queue();
    for (i = 0; i < n; i++)
        if (in_deg[i] == 0) q.push(i);
    ans = new vector();
    while (!q.empty()) {
        u = q.pop();
        ans.push_back(u);
        for each edge(u, v) {
            if (--in_deg[v] == 0) q.push(v);
        }
    }
    if (ans.size() == n) {
        for (i = 0; i < n; i++)
            std::cout << ans[i] << std::endl;
        return true;
    } else {
        return false;
    }
}

拓扑排序的阶过不唯一，所以一般会按某种要求进行输出，就需要用到优先队列，按字典序输出：

 1 vector<int> head[maxn],ans;
 2 int n,m,in[maxn];
 3 void topologicalsorting()
 4 {
 5     cin>>n>>m;
 6     for(int i=0; i<m; i++)
 7     {
 8         int u,v;
 9         scanf("%d%d",&u,&v);
10         head[u].push_back(v);
11         in[v]++;
12     }
13     priority_queue<int,vector<int>,greater<int> > q;
14     for(int i=1; i<=n; i++)
15     {
16         if(!in[i])
17         {
18             q.push(i);
19         }
20     }
21     while(q.empty()&&ans.size()<n)
22     {
23         int v=q.top();
24         q.pop();
25         ans.push_back(v);
26         for(int i=0; i<head[v].size(); i++)
27         {
28             in[head[v][i]]--;
29             if(!in[head[v][i]])
30              q.push(head[v][i]);
31         }
32     }
33     if(ans.size()==n)
34     {
35         //找到了排序
36     }
37     else
38     {
39         //图里有自环；
40     }
41     
42 } 

算法：（DFS）

DFS版本：

 

 1 // dfs 版本
 2 bool dfs(int u) {
 3   c[u] = -1;
 4   for (int v = 0; v <= n; v++)
 5     if (G[u][v]) {
 6       if (c[v] < 0)
 7         return false;
 8       else if (!c[v])
 9         dfs(v);
10     }
11   c[u] = 1;
12   topo.push_back(u);
13   return true;
14 }
15 bool toposort() {
16   topo.clear();
17   memset(c, 0, sizeof(c));
18   for (int u = 0; u <= n; u++)
19     if (!c[u])
20       if (!dfs(u)) return false;
21   reverse(topo.begin(), topo.end());
22   return true;
23 }

 

 

考虑一个图，删掉某个入度为  的节点之后，如果新图可以拓扑排序，那么原图一定也可以。反过来，如果原图可以拓扑排序，那么删掉后也可以。

 

练习：

1，判断自环问题：链接

题意：就裸拓扑排序，判断一下自环；

code:

 

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int maxn = 1e5+10;
 4 vector<int> G[maxn];
 5 int in[maxn];
 6 int n,m;
 7 int sum;
 8 queue<int> q;
 9 int toposort()
10 {
11     while(!q.empty())
12      q.pop();
13     sum=0;
14     for(int i=1; i<=n; i++)
15      if(!in[i])
16       q.push(i);
17     while(!q.empty())
18     {
19         int v=q.front();
20         q.pop();
21         sum++;
22         for(int i=0; i<G[v].size(); i++)
23         {
24             in[G[v][i]]--;
25             if(!in[G[v][i]])
26              q.push(G[v][i]);
27         }
28     }
29     if(sum==n)
30      return 1;
31     else
32     {
33         return 0;
34     }
35     
36 }
37 int main()
38 {
39     int t;
40     cin>>t;
41     while(t--)
42     {
43         cin>>n>>m;
44         memset(G,0,sizeof(G));
45         memset(in,0,sizeof(in));
46         for(int i=1; i<=m; i++)
47         {
48             int u,v;
49             cin>>u>>v;
50             G[u].push_back(v);
51             in[v]++;
52         }
53         if(toposort())
54          cout<<"Correct"<<endl;
55         else
56         {
57             cout<<"Wrong"<<endl;
58         }
59         
60     }
61     //system("pause");
62     return 0;
63 }

 

2，同1，判断自环，注意范围变了，从0~n-1；（HDU3342）

code：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int maxn = 1e5+10;
 4 vector<int> G[maxn];
 5 int in[maxn];
 6 int n,m;
 7 int sum;
 8 queue<int> q;
 9 int toposort()
10 {
11     while(!q.empty())
12      q.pop();
13     sum=0;
14     for(int i=0; i<n; i++)
15      if(!in[i])
16       q.push(i);
17     while(!q.empty())
18     {
19         int v=q.front();
20         q.pop();
21         sum++;
22         for(int i=0; i<G[v].size(); i++)
23         {
24             in[G[v][i]]--;
25             if(!in[G[v][i]])
26              q.push(G[v][i]);
27         }
28     }
29     if(sum==n)
30      return 1;
31     else
32     {
33         return 0;
34     }
35     
36 }
37 int main()
38 {
39     
40     while(cin>>n>>m)
41     {
42         if(!n&&!m)
43          break;
44         memset(G,0,sizeof(G));
45         memset(in,0,sizeof(in));
46         for(int i=1; i<=m; i++)
47         {
48             int u,v;
49             cin>>u>>v;
50             G[u].push_back(v);
51             in[v]++;
52         }
53         if(toposort())
54          cout<<"YES"<<endl;
55         else
56         {
57             cout<<"NO"<<endl;
58         }
59     }
60     system("pause");
61     return 0;
62 }