算法基础-树状数组

Posted 2021-02-13 gauss191

  今天我们分享一下树状数组，前置知识-了解树的结构，知道什么是左右儿子，各个节点的名称，也就是有点基础吧。今天以一个实际问题引出树状数组吧，中查询l-r的区间。（以B站大佬的课件为例子，可以关注下，在最后放上链接）

如果是暴力的话，显然时间复杂度是接受不了的（o(n方)),为了解决这个问题，我们就要用一些高级的数据结构。就是我们今天介绍的树状数组。

  首先看下树状数组是什么， 

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。

这种数据结构（算法）并没有C++和Java的库支持，需要自己手动实现。在Competitive Programming的竞赛中被广泛的使用。树状数组和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。相比较而言，树状数组效率要高很多。(百度上的）

  然后在介绍前缀和，b[1] = a[1],b[2] = a[1] + a[2],b[3] = a[1] + a[2] +a[3]........b[n] = a[1] + a[2] + a[3] + ..... + a[n].这就是前缀和的概念，其实树状数组就是在维护一个前缀和。

  再介绍lowbit函数，用于再左右儿子或者是父节点，伪代码为 return x & (-x),就是返回某个数二进制从右往左的第一个一所代表的数，x于lowbit函数的关系如下、

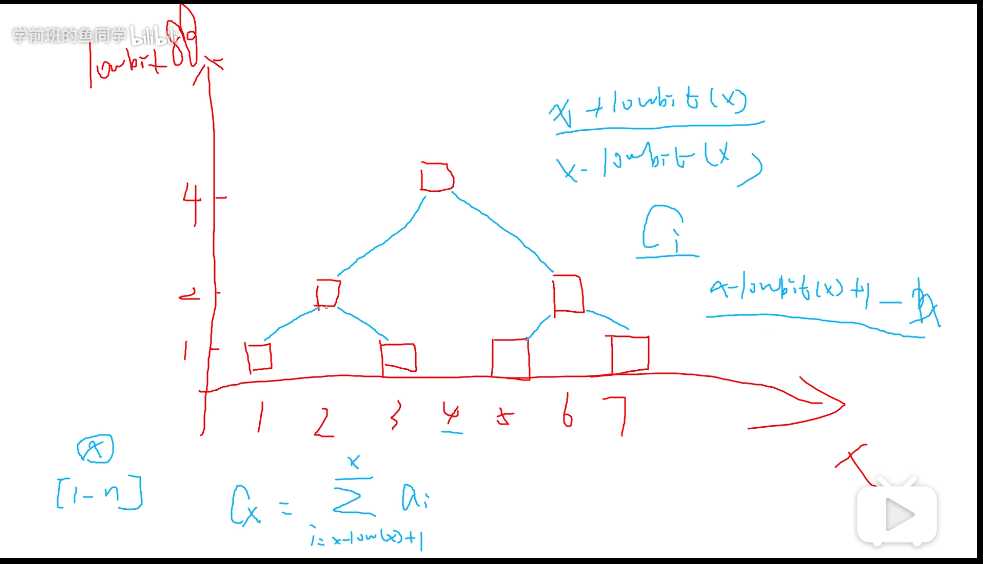
             一个左儿子的父节点表示为x + lowbit(x),同理右儿子的父亲表示为 x - lowbit(x),把图画出来，是不是很像二叉搜索树，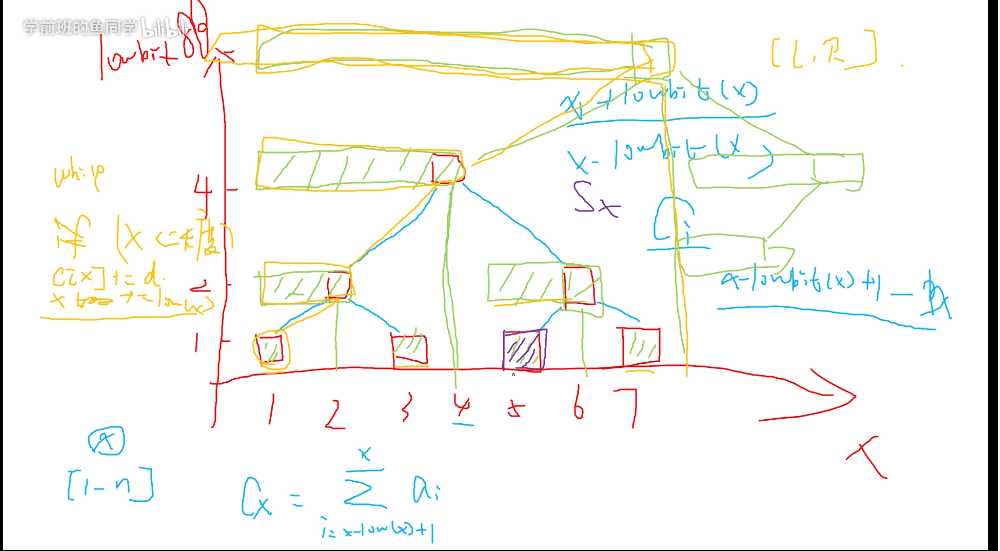

  最后，给个树状数组的模板题吧，

 

如题，已知一个数列，你需要进行下面两种操作：

 

1.将某区间每一个数加上x

 

2.求出某区间每一个数的和

 

输入输出格式

输入格式：

 

 

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

 

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

 

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

 

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

 

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

 

 

输出格式：

 

 

输出包含若干行整数，即为所有操作2的结果。（洛谷的题，https://www.luogu.org/problemnew/show/P3372）

输入样例

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例

11
8
20

附上AC代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 1e7 + 5;    
int n,m,a;
int d[N];     //存前缀和的数组

int lowbit(int x)
{
    return x & (-x);
}

int query(int x)  //查询操作
{
    int res = 0;
    while(x)    //x > 0,x从左边找父亲节点相加
    {
        res += d[x];
        x -= lowbit(x);
    }
    return res;
}

void add(int x,int val)
{
    while(x <= n)
    {
        d[x] += val;
        x += lowbit(x);   //从左到右构建树状数组
    }
}

int sum(int x)
{
    int total = 0;
    while(x != 0)
    {
        total += d[x];
        x -= lowbit(x);
    }
    return total;
}

int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n;i++)
    {
        cin >> a;
        add(i,a);
    }
    while(m--)
    {
        int f,x,y;
        cin >> f >> x >> y;
        if(f == 1)
        {
            add(x,y);
        }
        if(f == 2)
        {
            cout << sum(y) - sum(x - 1) << endl;
        }

    }
    return 0;

}

  最后的最后附上B站大佬的链接，https://www.bilibili.com/video/av36663299?from=search&seid=7911780148837730858