每日基础算法线段树 - 树状数组

Posted 2022-04-02 苏州程序大白

【每日基础算法】线段树 - 树状数组版

• 博主介绍
• 简介
• 原理
• 存储方式
• 操作
• 案例：动态求连续区间和
• 线段树
• 💫点击直接资料领取💫

博主介绍

🌊 作者主页：苏州程序大白

🌊 作者简介：🏆CSDN人工智能域优质创作者🥇，苏州市凯捷智能科技有限公司创始之一，目前合作公司富士康、歌尔等几家新能源公司

💬如果文章对你有帮助，欢迎关注、点赞、收藏（一键三连）和C#、Halcon、python+opencv、VUE、各大公司面试等一些订阅专栏哦

💅 有任何问题欢迎私信，看到会及时回复
💅关注苏州程序大白，分享粉丝福利

简介

线段树可以做很多事情，树状数组能做的线段树都能够实现。原理上线段树是一个非常简单的数据结构，但是在代码上比树状数组麻烦。线段树和树状数组都是维护一个序列，但是线段树可以进行的操作有很多，基本没有什么限制，不仅仅可以做单点，还可以做比如“区间的最大值”、“区间减法”、“染色”、“区间面积”、“长度”、“最大连续和”等等。

原理

线段树是一个完全二叉树的数据结构，对于每一个节点：

struct node 
    int l, r;
    int sum;
;

根节点存放的是所有数的总和。

比如一个[1, 7]这一个区间，根节点存放这七个数的总和28，每一个区间，如果长度不是1的话，就会尽量平均分成两份，比如这里我们分为[1, 4]，和[5, 7]。

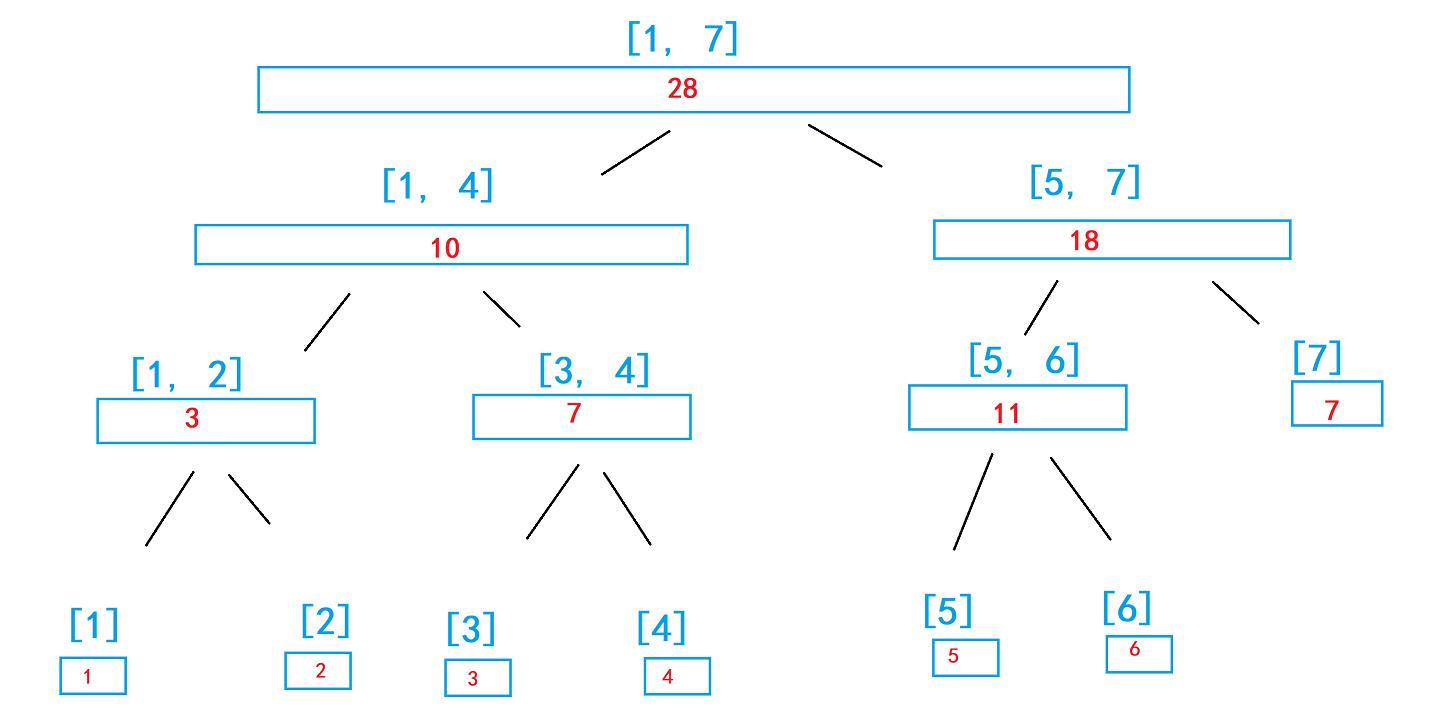
这个结构就相对简单了，每次对半开即可。

对于区间划分为两段的方法：

[L, R]划分为[L, Mid]与[Mid + 1, R]

其中$Mid = \\lfloor \\fracL+R2 \\rfloor$

存储方式

和堆类似，使用数组进行存储，且数组最大长度不会超过4N。

操作

单点修改O(logn)

作用：修改这段区间的某一个值，并更新线段树。

单点修改是一个递归的过程，只需要修改信息需要变化的节点（与修改节点相关的节点）即可，比如我们修改上图的5，我们只需要修改[1, 7]、[5, 7]、[5, 6]、[5]这4个节点即可。

区间查询O(logn)

作用：查询某一个区间的总和是多少。

区间查询也是一个递归的过程，比如求2 ~ 5这一段的区间是多少，我们是不断往下递归，直到完全包含这段区间位置。

四个函数

• pushup：用子节点信息更新当前节点信息

• build：在一段区间上初始化线段树

• modify：修改操作

• query：查询操作

案例：动态求连续区间和

给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列[a,b]的连续和。

输入格式

第一行包含两个整数n 和 m，分别表示数的个数和操作次数。

第二行包含n 个整数，表示完整数列。

接下来 m 行，每行包含三个整数 k, a, b（k = 0，表示求子数列[a, b]的和；k = 1，表示第 a 个数加 b）。

数列从 1开始计数。

输出格式

输出若干行数字，表示k=0时，对应的子数列[a, b] 的连续和。

数据范围

1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,

数据保证在任何时候，数列中所有元素之和均在int范围内。

输入样例

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出样例

11
30
35

线段树

#include <iostream> 
using namespace std;

const int N = 1e5 + 10;

int n, m;
int w[N];    // 权值

struct Node 
    int l, r;
    int sum;
tr[N * 4]; 


void push_up(int u) 
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;


// u 是根节点 
void build(int u, int l, int r) 
    if (l == r) tr[u] = l, r, w[r];
    else 
        // 赋左右边界初值
        tr[u] = l, r;

        // 左右孩子递归
        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);

        // 更新
        push_up(u);
    


int query(int u, int l, int r) 
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum;

    int sum = 0;

    // 判断是否有交集 
    int mid = tr[u].l + tr[u].r >> 1;
    if (mid >= l) sum = query(u << 1, l, r);
    if (mid < r) sum += query(u << 1 | 1, l, r);
    return sum;


void modify(int u, int x, int v) 
    if (tr[u].l == tr[u].r) tr[u].sum += v;
    else 
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        push_up(u);
    


int main() 
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);
    build(1, 1, n);

    int k, a, b;
    while (m --) 
        scanf("%d %d %d", &k, &a, &b);
        if (k == 0) printf("%d\\n", query(1, a, b));
        else modify(1, a, b);
     

    return 0;

💫点击直接资料领取💫

​ 这里有各种学习资料还有有有趣好玩的编程项目，更有难寻的各种资源。 ​ ​

❤️关注苏州程序大白公众号❤️
👇 👇👇