数据结构|-二叉查找树（二叉搜索树）的链式存储结构的实现

Posted 2021-02-07 wq-kingstrong

二叉排序树，又称为二叉查找树。

它或者是一棵空树，或者是具有下列性质的二叉树。

• 若它的左子树不为空，则左子树上所有的结点的值均小于根结构的值；
• 若它的右子树不为空，则右字数上所有结点的值均大于它的根结点的值；
• 它的左右子树也分别为二叉排序树。

优点：

• 1，排序方便
• 2，方便查找
• 3，方便插入和删除

 

---

 

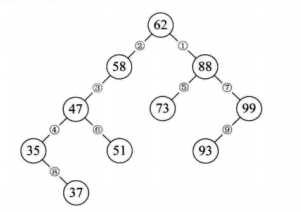
二叉排序树的插入数据：

因为二叉排序树中所有的数都符合排序树的特点，所以任意插入一个数时，都能在遍历树的过程中找到其应该放置的正确位置

 

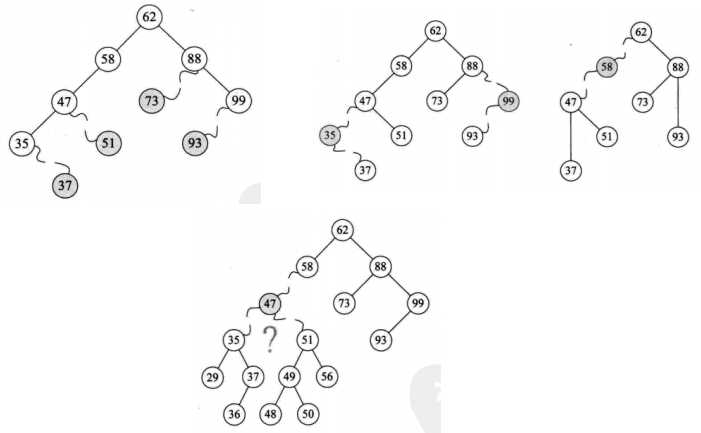
二叉排序树的删除数据：

三种情况：

• 1，叶子结点：直接删除该叶子（置空）
• 2，仅有左子树或者右子数的结点：将其子树的值赋给结点，删除这个子树
• 3，左右子树都有：找到结点的右子树中最小的结点（左子树的左的……的左子树）赋值给待删结点，然后删除那个最小的结点

---

 

 

 

 

---

 

代码部分：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace TestFun4
{
    class Program
    {
        static void Main(string[] args)
        {
            BSTree tree = new BSTree();
            int[] data = { 62, 58, 88, 47, 73, 99, 35, 51, 93, 37 };
            foreach (int item in data)
            {
                //将数组中的数装进树中去
                tree.Add(item);
            }
            Console.WriteLine("树的中序遍历：");
            tree.MiddleTravelsal();
            Console.WriteLine();
            Console.WriteLine("99是否存在树中：" + tree.Find(99));
            Console.WriteLine("11是否存在树中：" + tree.Find(11));
            tree.Delete(35);
            Console.WriteLine("删除35之后的中序遍历");
            tree.MiddleTravelsal();
            Console.WriteLine();
            tree.Delete(62);
            Console.WriteLine("删除62之后的中序遍历");
            tree.MiddleTravelsal();

            Console.ReadKey();
        }
    }

    /// <summary>
    /// 结点类、存储该结点的左子树、右子树、父亲
    /// </summary>
    class BSNode
    {
        public BSNode LeftChild { get; set; }
        public BSNode RightChild { get; set; }
        public BSNode Parent { get; set; }
        public int Data { get; set; }

        public BSNode() { }
        public BSNode(int item)
        {
            this.Data = item;
        }
    }

    class BSTree
    {
        BSNode root = null;

        //添加数据
        public void Add(int item)
        {
            //以该数据创建一个新结点
            BSNode newNode = new BSNode(item);
            //如果根节点为空，直接让插入的数据成为根节点
            if (root == null)
            {
                root = newNode;
            }
            else
            {
                BSNode temp = root;
                //遍历整棵树找到最适合插入数据的位置
                while (true)
                {
                    if (item >= temp.Data)//放在temp右边
                    {
                        if (temp.RightChild == null)//如果temp无右子树，就把newnode作为temp的右子树
                        {
                            temp.RightChild = newNode;
                            newNode.Parent = temp;
                            break;
                        }
                        else//否则继续往下遍历
                        {
                            temp = temp.RightChild;
                        }
                    }
                    else//放在temp左边
                    {
                        if (temp.LeftChild == null)
                        {
                            temp.LeftChild = newNode;
                            newNode.Parent = temp;
                            break;
                        }
                        else
                        {
                            temp = temp.LeftChild;
                        }
                    }
                }
            }
        }

        //中序遍历（中序遍历就是二叉排序树的从小到大排序）
        public void MiddleTravelsal()
        {
            MiddleTravelsal(root);
        }
        private void MiddleTravelsal(BSNode node)
        {
            if (node == null) return;
            MiddleTravelsal(node.LeftChild);
            Console.Write(node.Data + "  ");
            MiddleTravelsal(node.RightChild);
        }

        //判断树中是否已存在item这个值
        public bool Find(int item)
        {
            BSNode temp = root;
            while (true)
            {
                if (temp == null) return false;
                if (temp.Data == item) return true;
                if (item > temp.Data)
                    temp = temp.RightChild;
                else
                    temp = temp.LeftChild;
            }
        }

        //删除某个值所在的结点
        public bool Delete(int item)
        {
            BSNode temp = root;
            while (true)
            {
                //temp==null表示树中没有找到该值，返回false表示删除失败
                if (temp == null) return false;
                if (temp.Data == item)
                {
                    DeleteNode(temp);
                    return true;
                }
                if (item > temp.Data)
                    temp = temp.RightChild;
                else
                    temp = temp.LeftChild;
            }
        }
        //删除结点的具体操作
        private void DeleteNode(BSNode node)
        {
            //情况1：要删除的结点没有左右子树
            if (node.LeftChild == null && node.RightChild == null)
            {
                if (node.Parent == null)//删除根结点
                    root = null;
                else if (node.Parent.LeftChild == node)//要删除的结点是其父亲的左子树时候
                    node.Parent.LeftChild = null;//删除左子树就是删除该结点
                else if (node.Parent.RightChild == node)//右子树的情况
                    node.Parent.RightChild = null;
                return;
            }
            //情况2：要删除的结点有右子树没有左子树
            if (node.LeftChild == null && node.RightChild != null)
            {
                node.Data = node.RightChild.Data;//将其右子树作为被删除的这个结点
                node.RightChild = null;
                return;
            }
            //情况3：要删除的结点有左子树没有右子树
            if (node.LeftChild != null && node.RightChild == null)
            {
                node.Data = node.LeftChild.Data;
                node.LeftChild = null;
                return;
            }
            //情况4：要删除的结点有左右两个子树
            BSNode temp = node.RightChild;//找到右子树所包含的所有结点中最小的结点替换现在的结点
            while (true)
            {
                //左子树的左子树的左子树的…的左子树就是整个子树中最小的结点
                if (temp.LeftChild != null)
                    temp = temp.LeftChild;
                else
                    break;
            }
            node.Data = temp.Data;//数值替换
            DeleteNode(temp);//递归调用：把temp这个结点删除（因为temp无子树，所以会递归到情况1来删除这个结点）
        }

    }
}

---

结果：