线型代数
Posted nightbreeze
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线型代数相关的知识,希望对你有一定的参考价值。
行列式
- | A | = | AT |
- 对换行(列), 变号
- 两(列)相同, 等于0
- 某行乘以k, k 可提出。
- 第i行(列)是两个数之和,则是两个行列式之和
- 把1行(列)乘k加到另一行(列)行列式值不变。
- 行列式展开法则
| A | = ∑ a1j A1j, 代数余子式Aij = (-1) i+j Mij
- 范德蒙特行列式
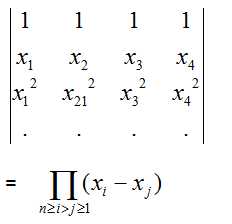
矩阵及运算
- 矩阵用于向量线型变换的系数, 如投影和旋转
- 单位矩阵 :E 和对角矩阵Λ: Diag(λ1,λ2, λ3, …) .
- 矩阵的相加 :
A+B = B + A
(A+B) + C = A + (B+C)
- 数乘 :λ A = A λ
- 矩阵相乘 : 左边为系数, 右矩阵为多个向量, 那么相乘的意义就是多个向量的的线性变换
(AB) C = A (BC)
λ (AB) = (λA)B
A(B+C) = AB + AC
- 矩阵的转置运算
(AT )T = A
(A+B)T = AT + BT
(λA)T = λAT
(AB)T = BT AT
- 对称AT=A, 元素沿着对角线相等
- 矩阵的行列式
|AT|=|A|
| λA| = λ|A|
|AB|=|A||B|
- 逆矩阵 : AB = BA =E , 则B = A-1
- 如A可逆, 则|A| ≠ 0
- 如果|A| ≠ 0,则A可逆, 且
![]() , 由代数余子式组成
, 由代数余子式组成
- |A| = 0, A 称为奇异矩阵, 否则非奇异矩阵
- 矩阵可逆的充分必要条件是 非奇异矩阵
- AB=E, B=A-1
- 矩阵逆运算
(A-1 )-1 = A
(λA)-1 = 1/λ A-1
(AB)-1 = B-1 A-1
- 矩阵的多项式:φ(A) = a0E + a1A + a2A2 + … + amAm
Φ(A) F(A) = F(A) Φ(A)
如果 A = PΛP-1, 则φ(A) = P φ(Λ) P-1 .
Λ是一个对角阵Λ: Diag(λ1,λ2, λ3, …) .
- 克拉默法则: 如果非齐次线型方程组 (Ax=b)的系数矩阵(方阵)A的行列式不等于0, |A|≠0, 则方程组有唯一解。
![]()
Aj 是矩阵A中第j列用常数项替换后的得到的 n 阶矩阵
- 逆阵方法:x = A-1b
- 矩阵分块
I分块相加
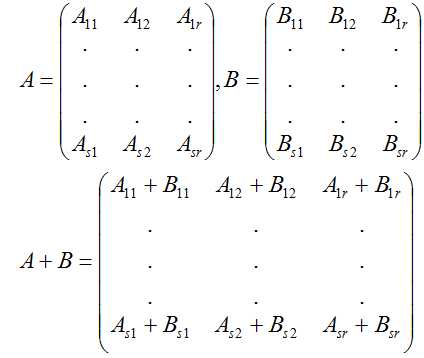
II分块数乘
Aλ =

III分块相乘
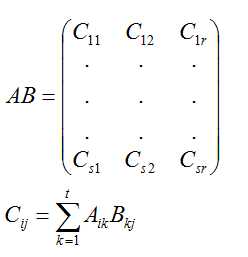
IV 矩阵转置

V 对角分块:
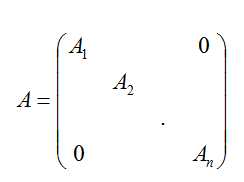
|A| = |A1| |A2| …|An|
矩阵的初等变换和线性方程组
- 矩阵的初等变换
I 兑换两行(列): ri ?rj
II 数乘k某行(列)ri ′k
III 把某一行(列)乘k再加到另外一行(列) ri + rj ′k
- 矩阵A做有限次初等变换变成B,称作等价
矩阵A与B行等价 , 记作![]()
矩阵A与B列等价 ,记作![]()
矩阵A与B列等价等价,记作 A~B
- 等价关系的性质
I 反身性A~A
II 对称性,如果A~B, B~A
II, 传递性, A~B, B~C, 则, A~C
- 行梯形矩阵 :倒梯形:i. 非0行在0行的上面,ii. 首非0元的下面为0 .
- 最简型 : i. 首非0元为1,ii. 非0元的后面都是0
- 设A与B为 m′n矩阵, 那么
( i)![]() 的充要条件是存在m阶可逆矩阵P, 是PA=B
的充要条件是存在m阶可逆矩阵P, 是PA=B
(ii) ![]() 的充要条件是存在n阶可逆矩阵Q, 是AQ=B
的充要条件是存在n阶可逆矩阵Q, 是AQ=B
(iii) A ~B的充要条件是存在m阶可逆矩阵及n阶可逆矩阵Q, P是AQ=B
- 单位矩阵E,经过一次初等变换得到的矩阵称为初等矩阵
- A 是一个m′n矩阵,对A施行一次初等变换相当于A左乘一个m阶初等矩阵; 对A实施一次初等列变换相当于A右乘一个n阶初等矩阵
(i) 到E的i,j两行对换得到初等矩阵E(i,j)
矩阵A的两行兑换≈ Em(i,j)A , 两列兑换≈AEn(i,j)
(ii) 行 数乘k ≈Em(i(k))A , 列 数乘k ≈En(i(k))A
(iii) A矩数乘k 到j行加到i行上去 ≈ Em(i,j(k))A
A矩数乘k 到i列加到j列上去 ≈A En(i,j(k))
- 初等矩阵都是可逆的
E(i,j) -1 = E(ii,j)
E (i(k))-1 = E (i(![]() ))
))
E(ij(k))-1 = E (ij(-k)
- 方阵A可逆的充要条件是存在有限个初等矩阵P1, P2, …Pl, 是A=P1P2 …Pl
- 方阵可逆的的充要条件是
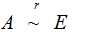
- 增广矩阵(A,E)经过初等行变换成为(E,P), 则P就是A-1
- 同理可以用作最简型的左乘矩阵
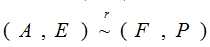 , PA=F
, PA=F - 解矩阵方程 AX=B, 因为X= A-1B,
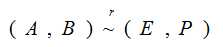 , 则P= A-1B=X
, 则P= A-1B=X
- 将矩阵初等行变换成阶梯形矩阵 ,矩阵的秩就是非0行的个数
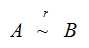 则A与B非0子式的最高阶相等
则A与B非0子式的最高阶相等
- R阶非0子式D是A的最好阶非0子式, r = R(A)
- 矩阵的秩的性质
1) 0 ≤ (Amxn ) ≤ min(m,n)
2) R (AT) = R(A)
3) 若A~B, 则 R(A) = R(B)
4) 若P,Q可逆, R(PAQ)=R(A)
5) Max(R(A), R(B)) ≤ R (A, B) ≤ R(A) + R(B)
6) R(A+B) ≤ R(A) + R(B)
7) R(AB) ≤ min(R(A), R(B))
8) 若AmxnBnxl = 0, R(A) + R (B) ≤ n
- N元线性方程组 Ax = b
无解的充要条件是 R(A) < R (A, b)
有唯一解的充要条件是R(A)=R(A,b) = n
有多个解的充要条件是R(A) = R (A, b) < n
有解的充要条件是R(A)=R(A,b)
- N元齐次线性方程组 Ax = 0有非0解的充要条件是R(A)<n
N元线性方程组 Ax = B, 有解的充要条件是R(A)=R(A,B)
向量组的线性相关性
- 几个有次序的数, a1, a2, …, an 所组成的数组称为n维向量。 这几个数称为n个分量。
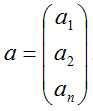 , 行向量用aT 表示。
, 行向量用aT 表示。
- 向量组: 若干同维数的列向量(行向量)组成的集合
- 向量的线型组合
k1a1 + k2a2 + k3a3 + … + kmam
- 向量 能由向量组A:a1, a2, …, an线型表示的充要条件是矩阵A =(a1, a2, …, an)的秩等于矩阵B=(A,b)的秩
- 向量组B能由A线型表示,A能由B线型表示,则称两个向量组等价
- 向量 组B:b1, b2, …, bl能由向量组A:a1, a2, …, an线型表示的充要条件是矩阵R(A) = R(A,B)
- A和B等价的充要条件是R(A) =R(B) = R(A,B)
- B 能有A线型表示的充要条件是R(B)≤R(A)
- k1a1 + k2a2 + k3a3 + … + kmam = 0 , 有非0解则向量组线型相关, 无非零阶解则线型无关。
- 能由向量组A:a1, a2, …, an线性无关的充要条件是R(A) = n, 线型相关的充要条件是R(A) < n
- 向量组A:a1, a2, …, am线型相关, 则能向量组B:a1, a2, …, am, am+1也线型相关。反之,B线性无关, A也线性无关
- M个n维向量组,当维数n小于向量个数m的时候, 必相关。N+1个n维向量组必相关。
- 向量组A:a1, a2, …, am线型无关, 则能向量组a1, a2, …, am, b线型相关, 则b必能由A现行表示,且表示式唯一。
- 向量组的秩:向量组中最大无关向量组中向量的个数。只含有0向量的向量组的秩为0
- 矩阵的秩等于列向量的秩,也等于行向量的秩。
- 齐次线性方程组的最大无关解称为该齐次线性方程组的基础解系
- 齐次线性方程组的通解为基础解系的任意线型组合:k1x1 + k2x2 + ..+ krxr
- m′n 矩阵A的秩R(A) = r, 则n元齐次线型方程组Ax=0的解集S的秩:R(S) = n-r
- 若Am′nBn′l = 0, R(A) + R (B) ≤ n : 因为R(B) ≤ n-r, R(A) 故R(A) + R (B) ≤ n
- 对于Ax=b, x= h1和, x= h2是方程组的两个解, 则x = h1-h2 是Ax=0的解
- , x= h是方程组Ax=b的解, x= x是Ax=0的解, 则x= h + x也是Ax=b的解。
- 向量空间 : 设V是n维向量的集合, 如果V非空集合, 而且集合V对于向量的加法和数乘两种运算封闭,则成集合V为向量空间。
- S = {x |Ax=0 }, 是一个向量空间 (齐次线型方程组的解空间)
- S = {x |Ax=b }, 不是一个向量空间
- 向量空间V1 和V2, 如果V1 íV2, V1 是V2的子空间。
- 向量空间V,内有a1, a2, …, ar, ? V, 且满足
- a1, a2, …, ar线性无关
- V中任何向量都刻由a1, a2, …, ar线性表示
a1, a2, …, ar称为向量空间V的一个基, r是向量空间维数, V称为r维向量空间
- 如果向量空间V取定一个基a1, a2, …, ar,那么V中任何一个向量都可唯一的表示为 x = λ1a1+ λ2a2+…+ λrar, λ1, λ2,.., λr称为向量在基a1, a2, …, ar上的坐标。
- 基坐标变换 公式:从基A变换到基B, Ax = B, x = A-1B, x称为过度矩阵
- 坐标变换公式:
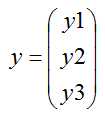 是 向量x在基A上的坐标,
是 向量x在基A上的坐标, 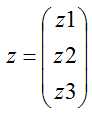 向量x在基B上的新坐标。x = Ay=Bz, 则z = B-1Ay
向量x在基B上的新坐标。x = Ay=Bz, 则z = B-1Ay
相似矩阵和二次型
- 向量的内积: [x,y] = x1y1 + x2y2 + … + xnyn
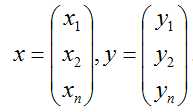 , [x,y] = xT y, 其结果是一个实数。
, [x,y] = xT y, 其结果是一个实数。
- 内积有下列性质
[x,y] = [y,x]
[λx,y] = λ[x,y]
[x+y,z] = [x,z] + [y,z]
当x=0时,[x,x]=0, 当x≠0时,[x,x] > 0
- 施瓦茨不等式
[x,y]2 ≤ [x,x] [y,y]
- 向量的数量积
x?y=|x||y|cos θ
- ||x|| =
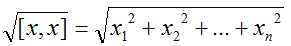 , 称为n为向量x的长度(范数)
, 称为n为向量x的长度(范数)
非负性, 当x=0时,||x||=0, 当x≠0时,||x|| > 0
齐次性 ||λx|| = |λ| ||x||
- 单位向量, ||x|| = 1 , 单位化 x =
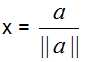
- 由施瓦茨(Schwarz)不等式,
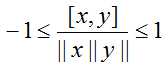 ,当x≠0而且,y≠0时cosθ =
,当x≠0而且,y≠0时cosθ =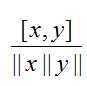
- 当[x,y]=0,x与y正交
- 正交向量组,两两正交的非0向量组
- 正交向量组a1, a2, …, ar,线性无关
- N 维向量a1, a2, …, ar是向量空间V(
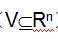 )的一个基,如果两两正交,而且都是单位向量,称为标准正交基
)的一个基,如果两两正交,而且都是单位向量,称为标准正交基 - 施密特(Schmidt)正交化
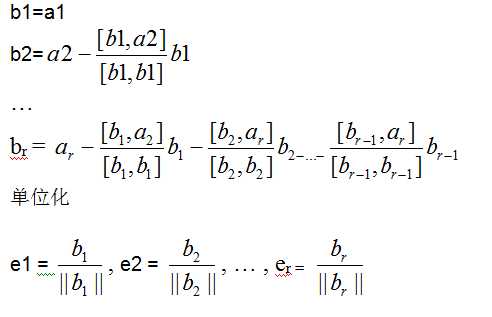
- 如果n阶矩阵A满足, ATA=E, (即A-1 = AT). 那么A为正交矩阵, 简称正交阵。
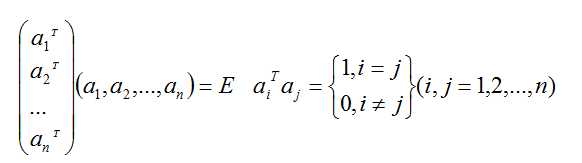
- 正交阵的充要条件是A的列向量都是单位向量而且两两正交。
- 如果P是正交阵, y=Px, 称为正交变换。
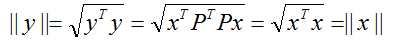
正交变换,向量长度保持不变(从而三角形的形状保持不变:加入两个向量同时做正交变换), 这是正交变换的优良特性。
- 设A是n阶矩阵, 如果数λ和n维非零列向量是关系式成立
Ax = λx, 那么这样的数λ,称为矩阵A的特征值, 非零向量x称为A的对应于λ的特征向量。
关系式也可写成(A-λE)x = 0, 它有非零阶的充要条件是|A-λE| = 0
- 特征方程:|A-λE| = 0, 特征多项式:|A-λE|, A的特征值就是特征方程的解 。特征方程在附属范围内恒有解, 其个数为方程的次数, (重根按重数计算), 因此, 方程有n个特征值。
- 设n 阶矩阵A = (aij)的特征值为λ1,λ2…,,λn, 则
λ1+λ2+…+λn = a11 + a22+…+ann,
λ1λ2…λn = |A|
- λ是方阵A的特征值,则
λ2 是A2的特征值
当A可逆的时候,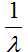 是A-1的特征值
是A-1的特征值
- λ1,λ2…,,λn是方阵A的特征值, p1, p2,.. pn 依次是与之对应的特征向量。 如果λ1,λ2…,,λn各不相同,则p1, p2,.. pn 线性无关 。
- A, B都是n阶矩阵, 若有可逆矩阵 P, 使 P-1AP=B, 则称B是A的相似矩阵 。P-1AP称为对A进行相似变换, P为相似变换矩阵
- 若n阶矩阵A和B相似, 则A和B的特征多项式相同,从而A与B的特征值相同。
- 若n阶矩阵A和对角阵Λ相似, 则λ1,λ2…,,λn,是A的n个特征值
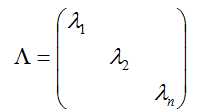
- 若A = PBP-1, 则Ak= PBkP-1, φ(A) = P φ (B)P-1, 对于对角阵:
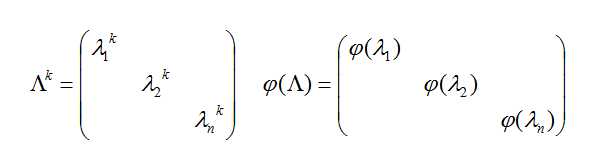
- 对于n阶矩阵A, 寻求变换矩阵P,使 P-1AP=, 称作把A对角化。
P-1AP==>
AP = P=>
A(p1,p2,…,pn) = (λ1p1, λ1p2,…, λ1pn) =>
Api = λipi (i=1,2,…n) => λi 是特征值,pi是与之对应的特征向量 。
P就是由n个特征向量组成的方阵。=>
P是否可逆?即是否线型无关=>
如果可逆,便有P-1AP=, 集A与对角阵相似。
- 对于n阶矩阵A与对角阵相似的充要条件是A有n个线性无关的特征向量。
- 如果特征值无不相等, 则A与对角阵相似
- 对阵矩阵
特征值为实数
特征值不同,则特征向量正交
- A是n阶对称矩阵, 则必有对角阵与其相似。对角阵的对角元素是A的特征值
- A是n阶对称矩阵, λ是k重根,则R(A- λE)=n-k, 从而λ有k个对应的线型无关的特征向量。
以上是关于线型代数的主要内容,如果未能解决你的问题,请参考以下文章