2018 10-708 (CMU) Probabilistic Graphical Models {Lecture 5} [Algorithms for Exact Inference]

Posted 2021-02-01 ecoflex

 

 Not in the frontier of research, but the results are used commonly now.

 

X_{k+1} - X_n are known,

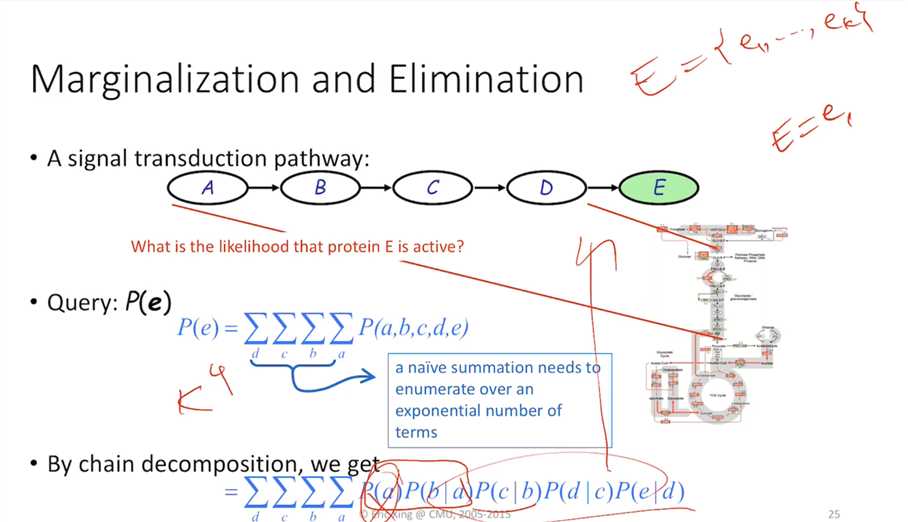
to calculate the joint probability, we have to do inference

 

 

 

 

 

 

 Recent research: on the approximate inference teches

 

approx:

1) optimization-based

2) sampling-based

 

 

 

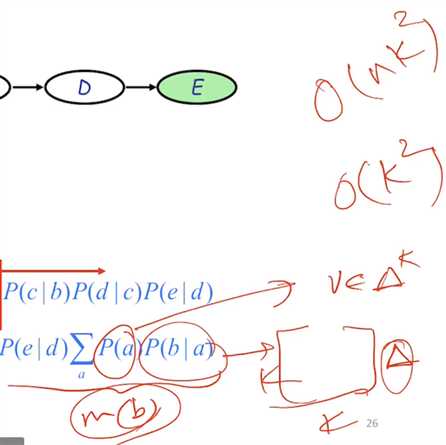
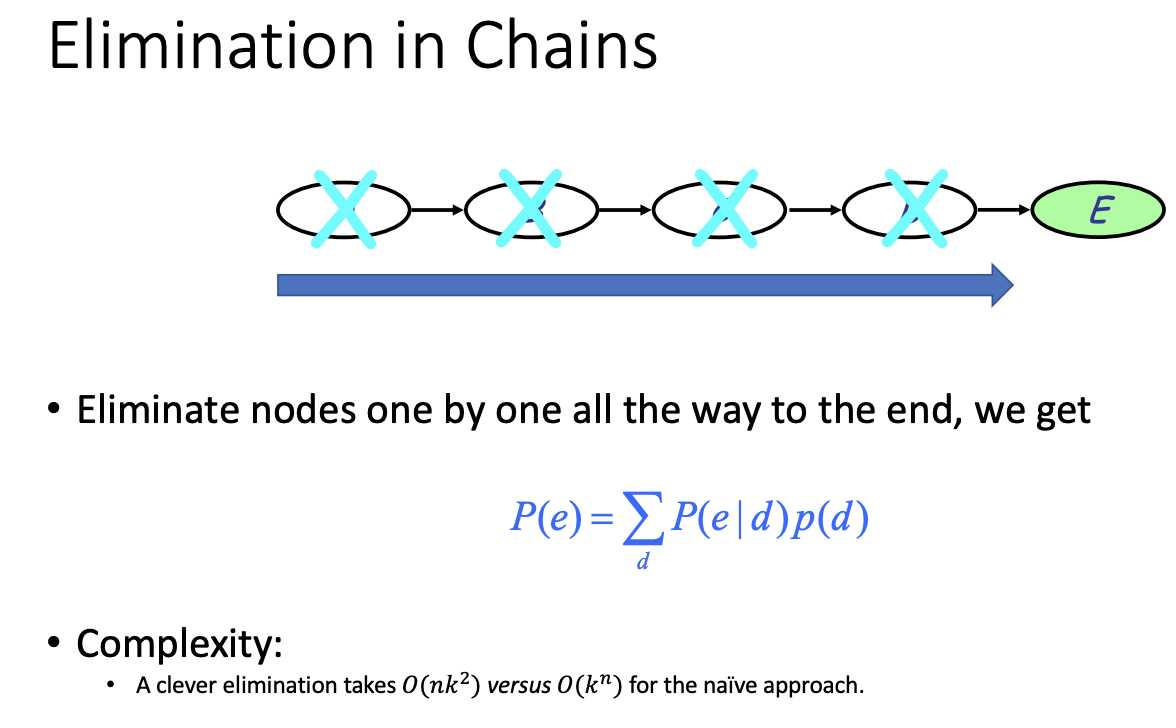
Compare the computational complexity:

    NAIVE way: K^n

    Chain rule:  n*K^2

    n=4

 

 

Chain rule derivation:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

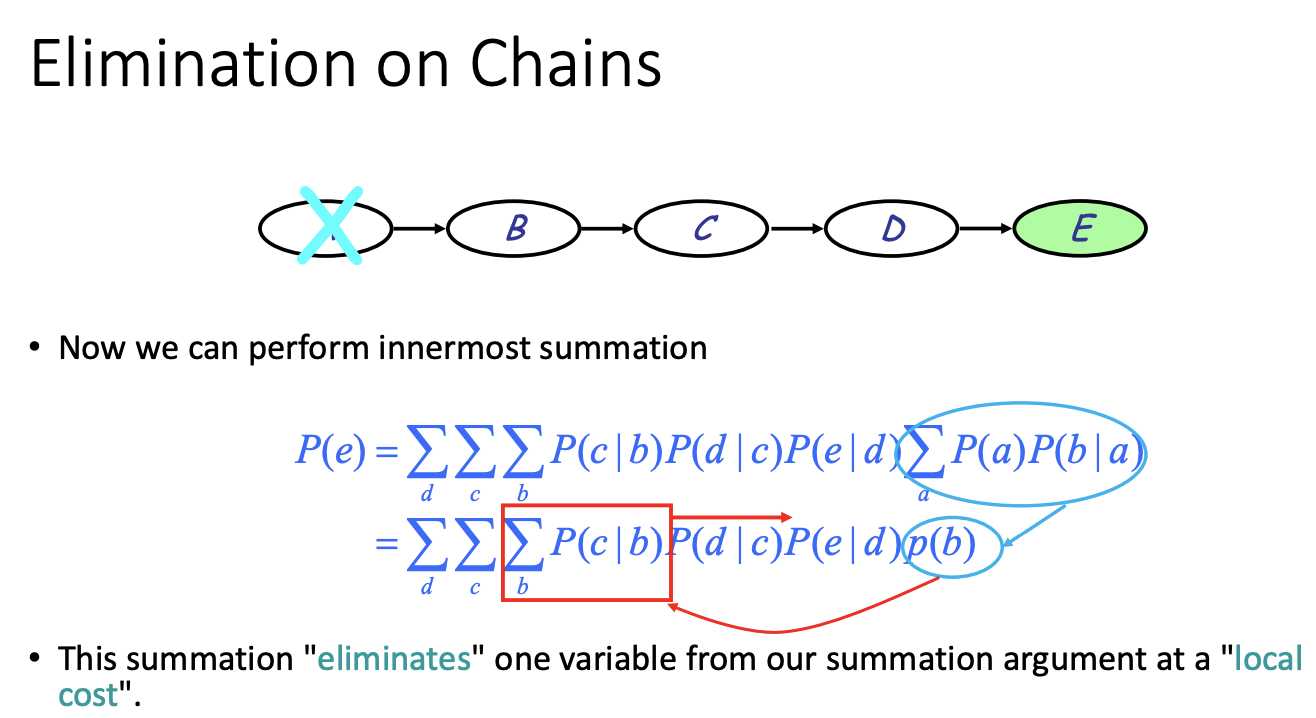
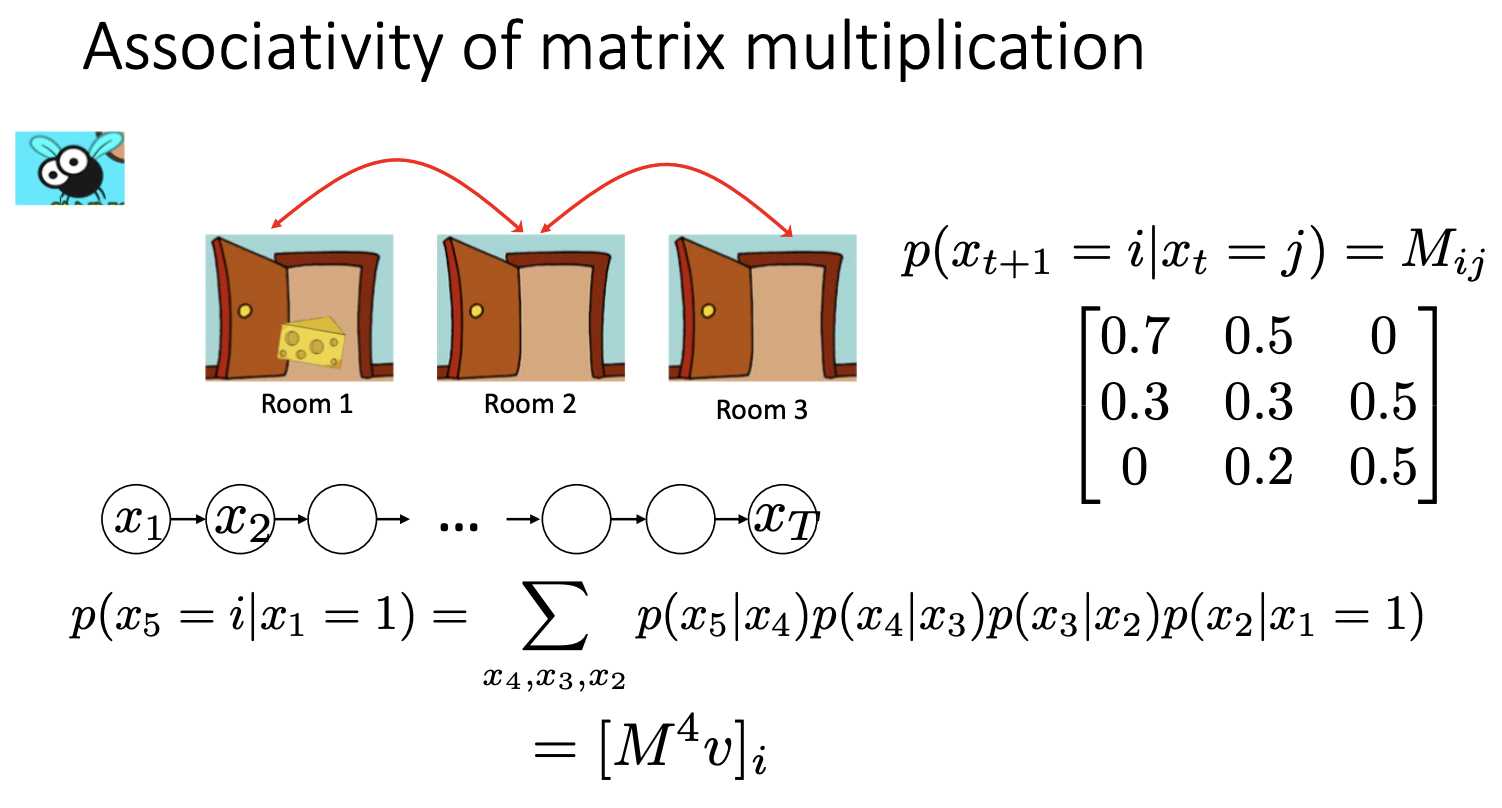
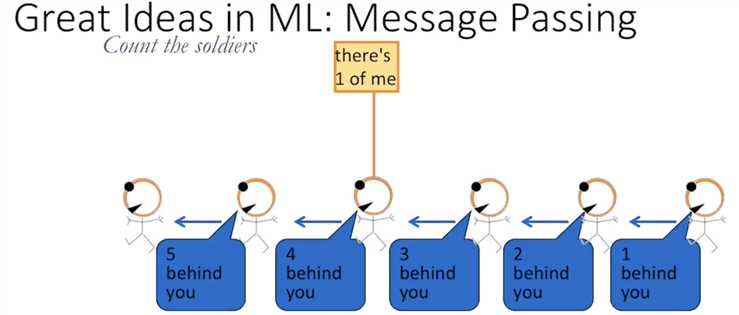
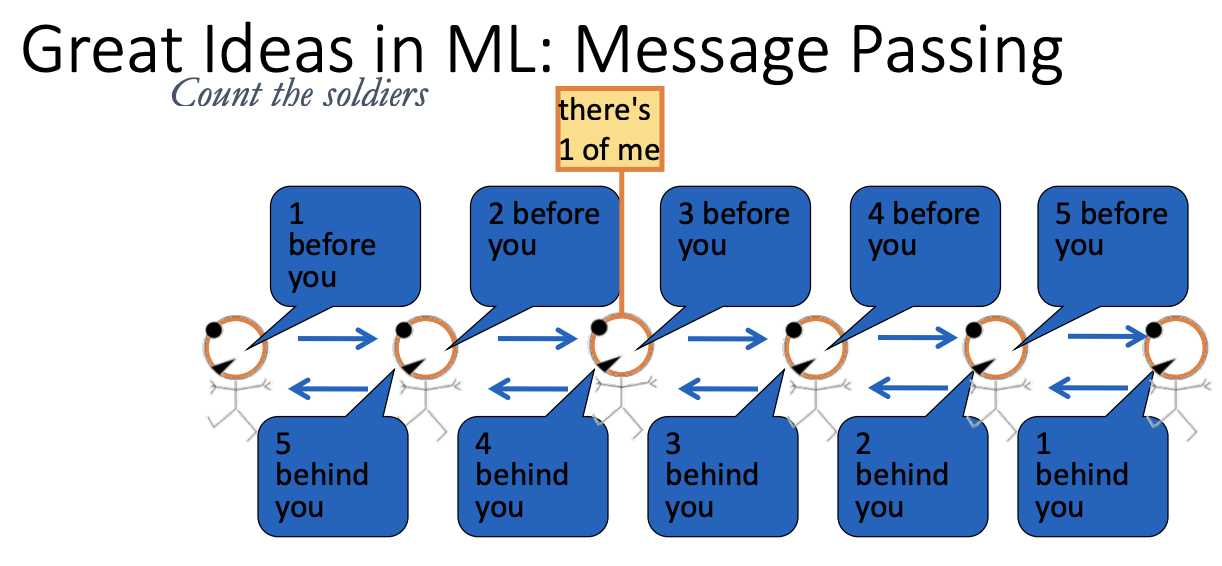
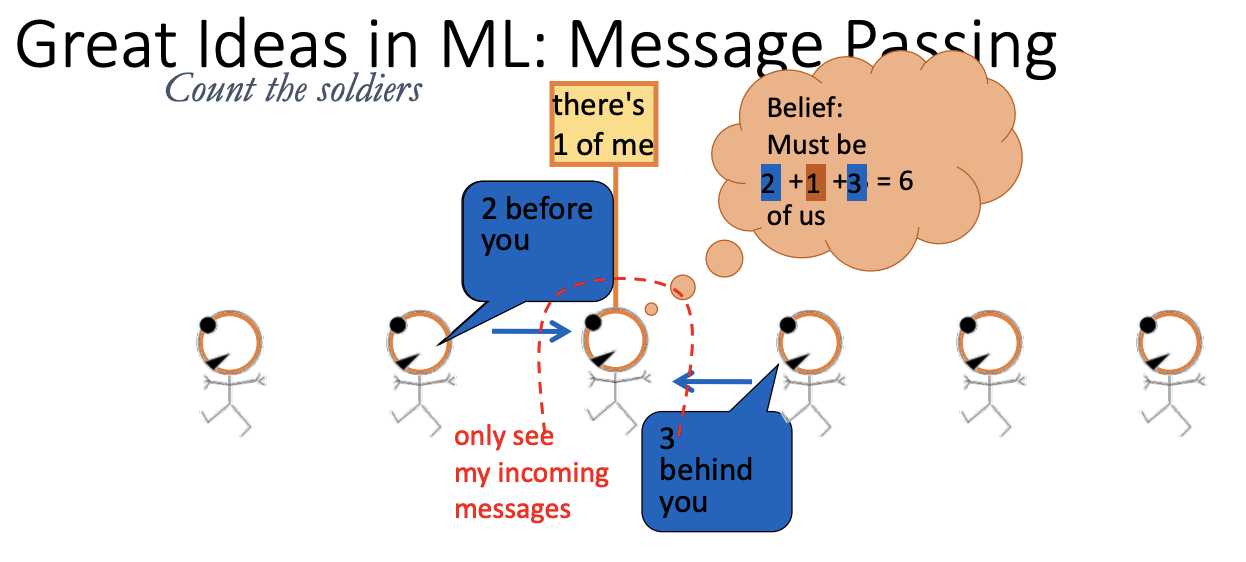
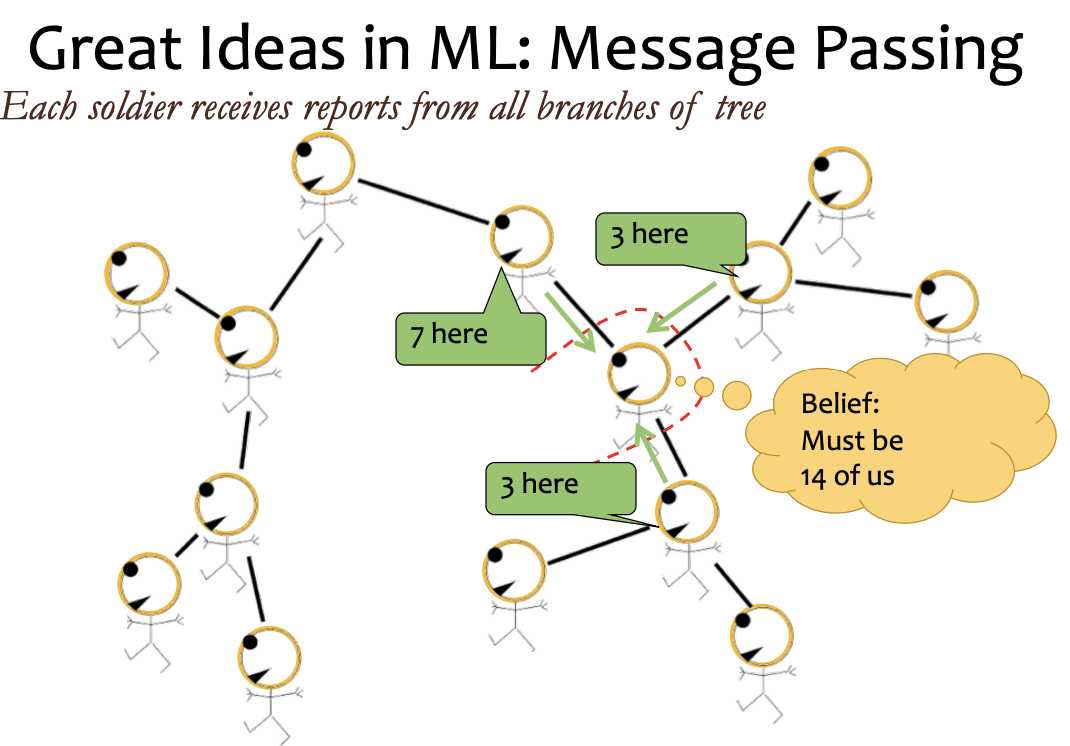
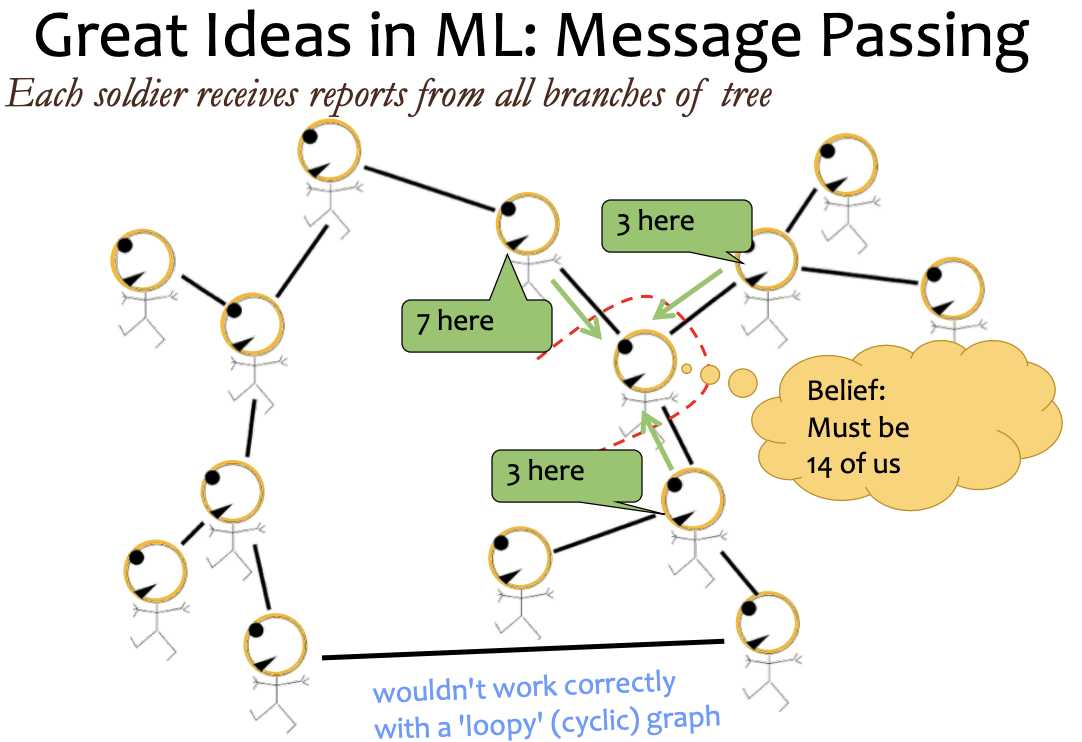
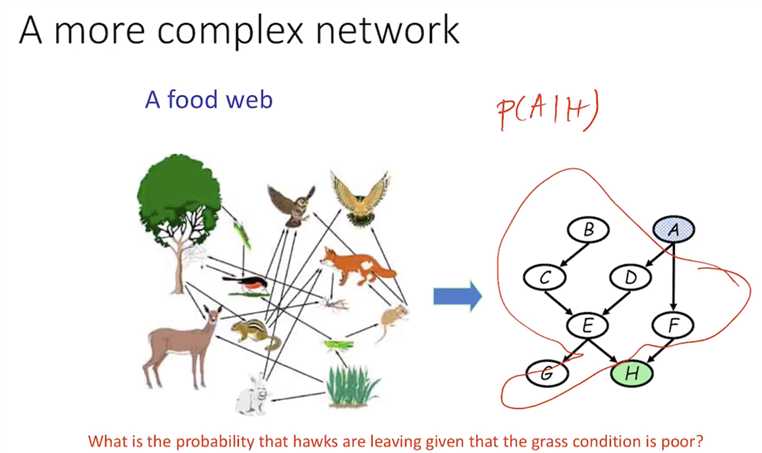
marginalizing out the rest 

 

 P(a) P(b) P(c|b) ...... P(h|e,f) => a,b,c,d,e,f,g,h (elimation sequence)

 

introduce a term m_h(e,f) to make e and f dependent

 

not introducing any dependency here

 

 

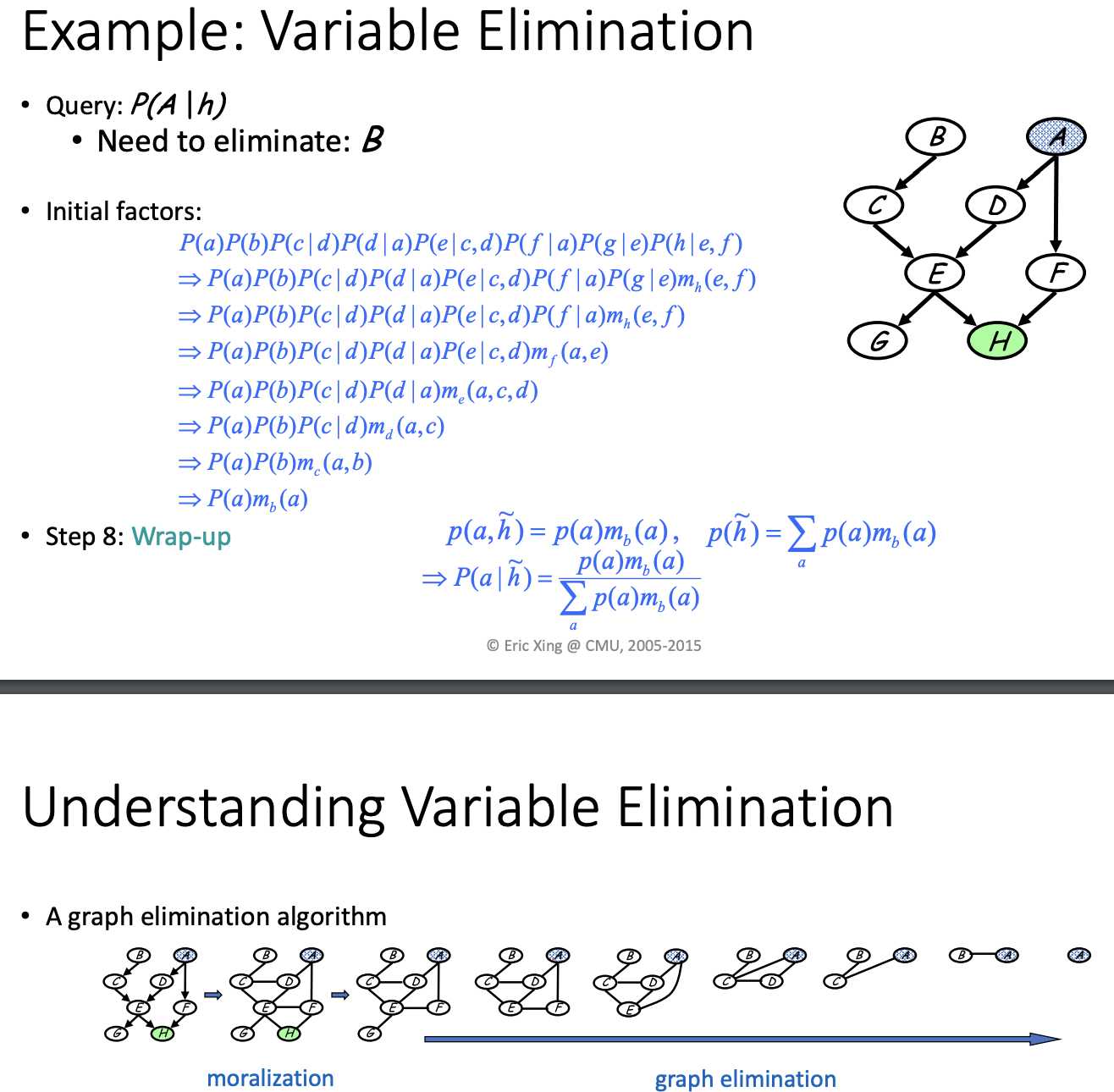
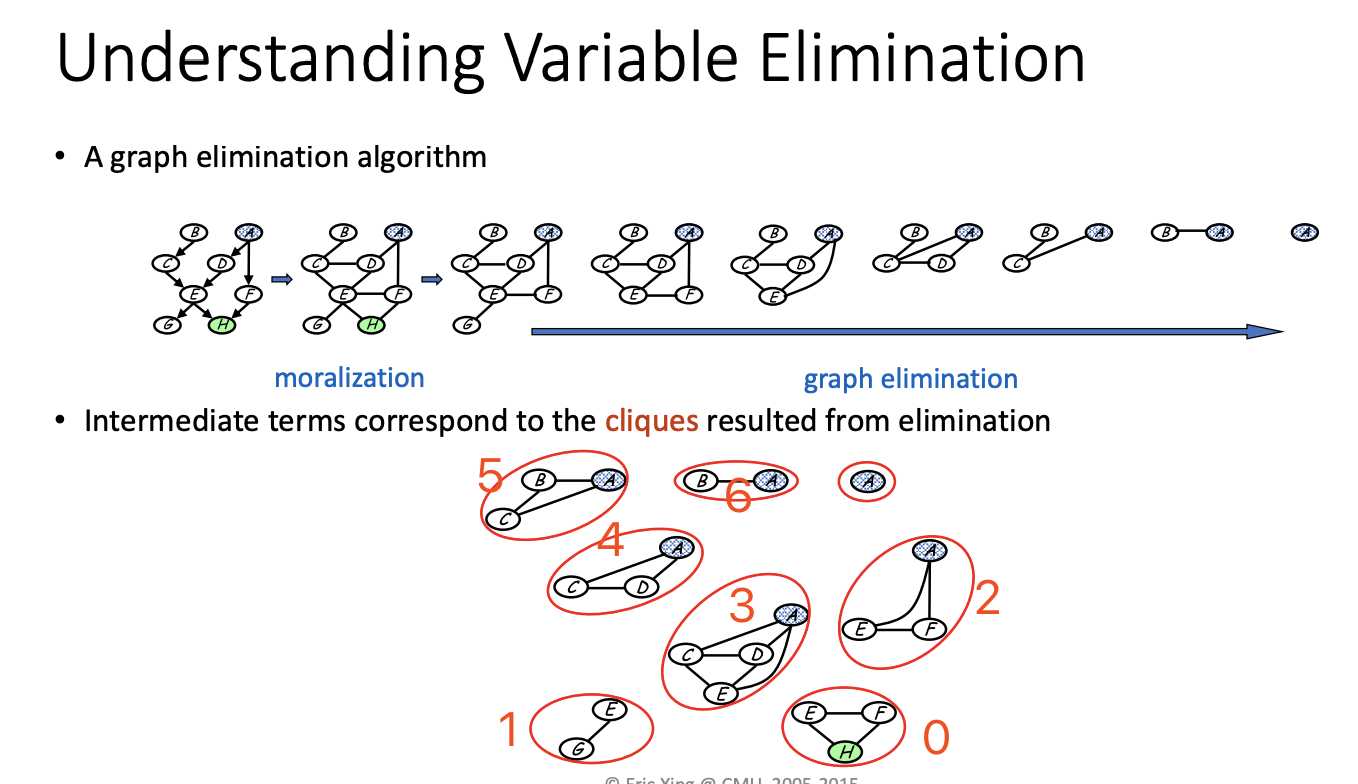
Different elimination sequence will lead to different computational complexity.

It‘s dependent on how large the new clique is

In one step, if you connect every vertex, then you are in trouble.

 

 

 

 

 

  

 

 

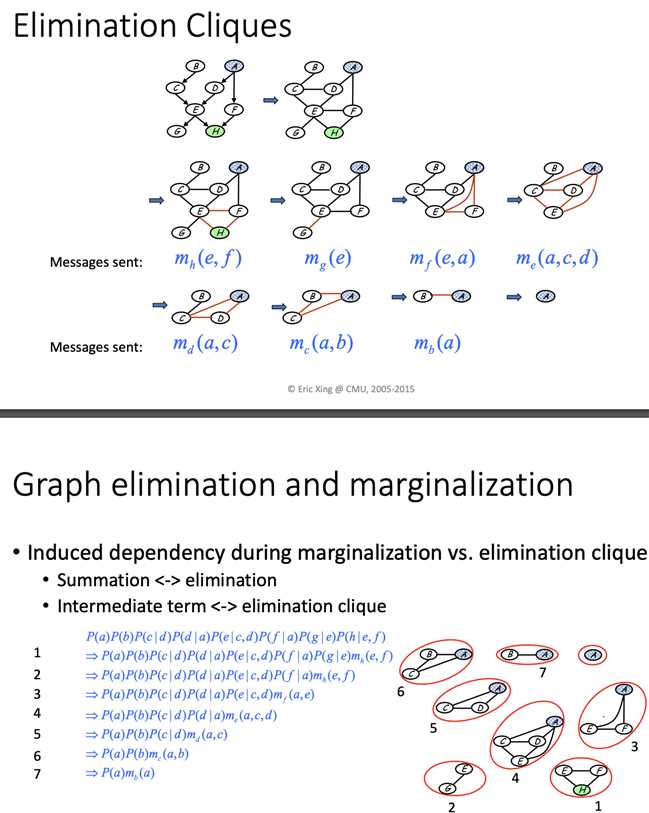
if there‘s a loop in graph, you can‘t view message passing as a variable to another variable, but clique to clique.