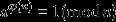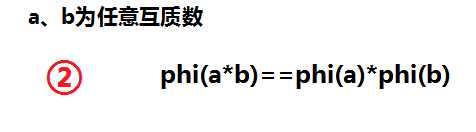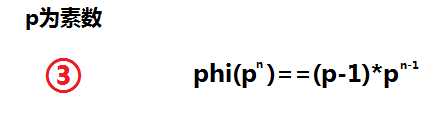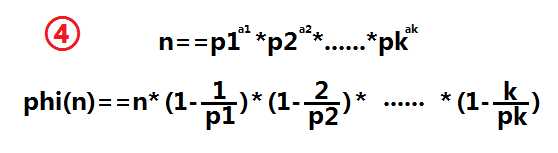数学数论初探欧拉定理

Posted 2021-01-27 antigonae

写在前面：

　　记录了个人的学习过程，同时方便复习

　　整理自网络

　　非原创部分会标明出处

 

目录 结论 证明 拓展 简化幂的模运算

 

 

结论

在数论中，欧拉定理(也称费马-欧拉定理或欧拉函数定理)是一个关于同余的性质 欧拉定理表明，若n，a为正整数，且n，a互质，则: ——bia度百科

 

证明

 　　(某一种证法)

 

　　将1~n中与n互质的数按顺序排布：x1,x2……xφ(n) （显然，共有φ(n)个数）

欧拉函数 　　在数论，对正整数n>1，欧拉函数是小于n的正整数中与n互质的数的数目(φ(1)=1) (其中p1, p2……pn为x的所有质因数，x是不为0的整数) ——bia度百科

　　我们考虑这么一些数：

　　m₁ == a*x₁　　m₂ == a*x₂　　m₃ == a*x₃　　……　　m_φ(n) == a*x_φ(n)

　　1）这些数中的任意两个都不模n同余，因为如果有m_S ≡ m_R (MOD n) (这里假定m_S更大一些)，就有：

　　m_S - m_R == a(x_S - x_R) == q_n，即n能整除a(x_S - x_R)

　　但是a与n互质，而x_S - x_R<n，因而左式不可能被n整除

　　也就是说这些数中的任意两个都不模n同余，φ(n)个数有φ(n)种余数

——bia度百科

 

拓展

• 简化幂的模运算

　　如计算7²²²的个位数，实际是求7²²²被10除的余数

　　7和10互素，且φ(10)=4

　　由欧拉定理知7⁴ Ξ 1 (MOD 10)

　　所以7²²² == (7⁴)⁵⁵ * (7²) Ξ 1⁵⁵ * 7² Ξ 49 Ξ 9 (mod 10)

 ——bia度百科