数据结构——树状数组

Posted 2021-01-25 ackers

我们今天来讲一个应用比较广泛的数据结构——树状数组

它可以在O（nlogn）的复杂度下进行单点修改区间查询，下面我会分成三个模块对树状数组进行详细的解说，分别是树状数组基本操作、树状数组区间修改单点查询的实现、树状数组查询最值的实现

 

---

一.

树状数组一般分为三种操作，初始化、修改、查询

在讲基本操作之前，我们先来看一张图

 

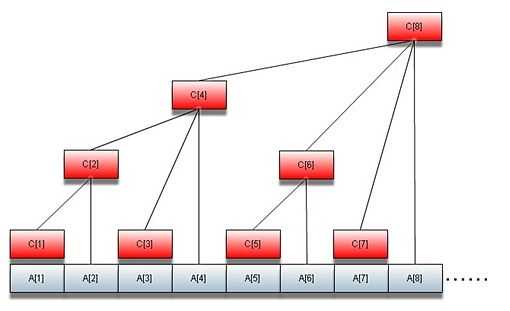
这张图就是树状数组的存储方式，对于没有接触过树状数组的人来说看懂上面这张图可能有些困难，上图的A数组就是我们的原数组，C数组则是我们需要维护的数组，这样存储能干什么呢，比如我们在查询A[1~7]数组的前缀和时，可以将C[4]、C[6]、C[7]三个数组的值加起来，那么它就是我们要求的A[1~7]的前缀和，那么为什么是C[4]、C[6]、C[7]三个数组呢

我们来看一下4、6、7在二进制下是什么

7 = 2² + 2¹ + 2⁰  = （111）₂

6 = 2² + 2¹  = （110）₂

4 = 2² = （100）₂

于是我们发现，从7到4，我们的二进制的1从最后一位开始减少，再根据上图，我们可以发现，C[i]数组存储区间为[ i - 2^k + 1,i]，其中k是二进制下i末尾的1

那么我们如何来求这个末尾的1呢，这里我们用了lowbit（x）表示x在二进制下末尾的1，lowbit的求法如下：

inline int lowbit(int x)
{
  return x&(-x);
}

那么为什么可以用x & (-x)求出lowbit，这要从二进制负数存储方法开始说了

二进制下的负数是将原来的整数取反后加1表示的，就像这样：

原数字x：（100101000）₂

取反~x：（011010111）₂

负数~x+1：（011011000）₂

我们发现，这样操作后，末尾1前面的数都被取反了，而后面的数全部变成了0，于是

x & (-x) = （000001000）₂

这样，我们就将二进制下的末尾1求出来了

下面我们讲树状数组的基本操作

 

inline void add(int x,int y) //给x加上y
{
  while(x <= n)
  {
    c[x] += y;
    x += lowbit(x);
  }
  return ;
}

inline int query(int x) //查询1~7的前缀和
{
  int ans = 0;
  while(x)
  {
    ans += c[x];
    x -= lowbit(x);
  }
  return ans;
}

 

当我们求区间l ~ r的区间和时，可以用C[r] - C[l - 1]

如果你还是不太懂，就结合着上面的图和代码，感性理解一下理解

 

---

 

二.

下面我们讲树状数组如何做到区间修改（单点查询过于简单我就不提了）

我们可以发现，当我们让区间l ~ r加上v时，实际上相当于我们先将区间l ~ n加上v，再将区间r + 1 ~ n减去v

所以，第一种方法，我们可以再维护一个树状数组B用来存区间修改的情况，当我们查询某一点i时，用B[1~i]的前缀和加上我们原来维护的数组，就可以做到区间修改单点查询了

不过，在这里我们有一种巧妙的方法可以不用维护两个树状数组，我们可以维护一个差分数组C，让A[i] - A[i - 1]加入数组C，这样我们在修改区间l ~ r时，只要让l加上v，再让r + 1减去v就行了，证明非常简单，因为l ~ r中的数同时加上了一个数，A[i] - A[i - 1]不变

这样我们就用一个树状数组进行了区间修改单点查询操作，在查询一个数x时，A[x]就是C[1~x]的前缀和

有一道洛谷的板子题可供练习

洛谷 P3368

代码如下：

 

#include <cstdio>
#include <cstring>
#include <algorithm>

const int maxn = 1e6 + 6;
int n,m;
int cost[maxn];

inline int read()
{
  char ch = getchar();int x = 0,f = 1;
  while(ch<‘0‘||ch>‘9‘){if(ch == ‘-‘) f = -1; ch = getchar();}
  while(ch>=‘0‘&&ch<=‘9‘){x = x*10 + ch -‘0‘; ch = getchar();}
  return x*f;
}

inline int lb(int  x)
{
  return x&(-x);
}

inline void add(int a,int v)
{
  while(a<=n)
  {
    cost[a] += v;
    a += lb(a);
  }
}

inline int query(int a)
{
  int ans = 0;
  while(a)
  {
    ans += cost[a];
    a -= lb(a);
  }
  return ans;
}

int main(int argc, char const *argv[]) 
{
  n = read();
  m = read();
  int pre = 0;
  for(int i = 1;i <= n;i ++)
  {
    int val = read();
    add(i,val - pre);
    pre = val;
  }
  for(int i = 1;i <= m;i ++)
  {
    int flag,x,y,k;
    flag = read();
    if(flag == 1)
    {
      x = read();
      y = read();
      k = read();
      add(x,k);
      add(y+1,-k);
    }
    else
    {
      x = read();
      printf("%d
",query(x));
    }
  }
  return 0;
}

 

 

---

 

三.

下面我们来讲树状数组查询区间最值，虽然它的复杂度为O（nlognlogn），但是依然是我们可以接受的

我们来考虑如何维护最值，一个显然的方法我们对于每个元素都让它自身的值和覆盖它的C数组取最值，复杂度为O（nlogn），然后当我们要改变一个数的值的时候，将C数组清空然后重新维护，显然这个复杂度并不理想

我们接着考虑有没有更快的维护方法，于是我们发现，对于一个区间C[x]，能转移到它的只有C[x - 2⁰]、C[x - 2¹]、C[x - 2²]...C[x - 2 ^k],且2^k < lowbit(x),2^k+1 >= lowbit(x)

这样，我们就维护出区间C[x]的最值了，且维护的复杂度为O（lognlogn）

代码如下：

inline void modify(int x,int y) //把x的值改为y
{
  a[x] = y;
  while(x <= n)
  {
    c[x] = a[x];
    for(int i = 1;i < lowbit(x);i <<= 1) c[x] = std::max(c[x],c[x - i]);
    x += lowbit(x);
  }
  return ;
}

查询的方法也非常简单，我们从查询的右端点开始找被包含的C数组，若r - lowbit(r) >= l，就用C[r]维护最值，否则，我们就直接用A[r]维护最值

代码如下：

inline int query(int l,int y) //查询区间l ~ r的最大值
{
  int ans = 0;
  while(l <= r)
  {
    ans = std::max(ans,a[r]);
    r--;
    while(l <= r - lowbit(r))
    {
      ans = std::max(ans,c[r]);
      r -= lowbit(r);
    }
  }
  return ans;
}

这里有一道例题

HDU 1754

就是一个树状数组维护最值的板子题，代码如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

const int maxn = 2e5+5;
int n,m;
int a[maxn];
int cost[maxn];

inline int lb(int x)
{
    return x&(-x);
}

inline void modify(int x)
{
    while(x<=n)
    {
        cost[x] = a[x];
        for(int i = 1;i < lb(x);i<<=1) cost[x] = std::max(cost[x],cost[x-i]);
        x += lb(x);
    }
}

inline int query(int l,int r)
{
    int ans = 0;
    while(l <= r)
    {
        ans = std::max(ans,a[r]);
        r --;
        while(l <= r-lb(r)) 
        {
            ans = std::max(ans,cost[r]);
            r -= lb(r);
        }
    }
    return ans;
}

int main()
{
    while(scanf("%d %d",&n,&m)!=EOF)
    {
        memset(a,0,sizeof(a));
        memset(cost,0,sizeof(cost));
        for(int i = 1;i <= n;i ++)
        {
            scanf("%d",&a[i]);
            modify(i);
        }
        for(int i = 1;i <= m;i ++)
        {
            char flag = getchar();
            while(flag!=‘Q‘&&flag!=‘U‘)flag = getchar();
            if(flag==‘Q‘)
            {
                int l,r;
                scanf("%d %d",&l,&r);
                printf("%d
",query(l,r));
            }
            else if(flag==‘U‘)
            {
                int x,v;
                scanf("%d %d",&x,&v);
                a[x] = v;
                modify(x);
            }
        }
    }
    return 0;
}