树状数组

Posted 2020-11-21 liuwenyao

说起树状数组，那就不得不提到线段树，它们可以说都可以完成区间修改和区间查询，但是树状数组的常数小，还好写，但是缺点是不能实现其他的高端操作，因此我们应该把这两种方法都掌握。对于那些简单的操作，可以用树状数组来写，反之就得用线段树了。

树状数组的主要思想跟线段树差不多，都是采用分治，但是他们的代码实现并不一样，主要是线段树是真真正正的树形结构，而树状数组则是虚拟的树形结构。

比如下面的这张图：

 

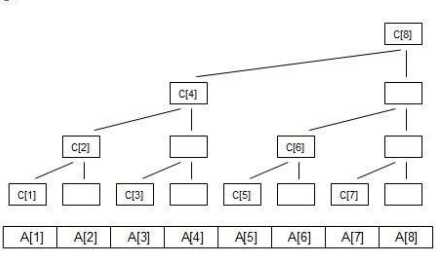
A数组是我们输入的数据，C数组便是我们的树状数组。

我们可以看到，树状数组的个数跟我们的输入数据的个数一样。

但是线段树却比树状数组用的空间大。

且我们可以找规律：

c1=a1;

c2=a1+a2;

c3=a3;

c4=a1+a2+a3+a4;

这个似乎看不出来关系，但是我们可以把数字转变为二进制。

c0001=a0001

c0010=a0001+a0010

c0011=a0011

c0100=a0001+a0010+a0011+a0100

我们就可以看出C[这个数的下标再加上该数二进制从右数第一个1位的右边的数的和]+=C[这个数]。

这个搞明白了，那单点修改就会了，如果我们想区间查询，那可以用前缀和维护。

代码(luoguP3374)：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define lowbit(x) (x&-x)
int a[1000100],ans[1000010],n,m,b;


void update(int x,int y)
{
    while(x<=n)
    {
        ans[x]+=y;
        x+=lowbit(x);
    }
} 
int query(int x,int y)
{
    
}
int query(int x)
{
    int sum=0;
    while(x!=0)
    {
        sum+=ans[x];
        x-=lowbit(x);
    }
    return sum;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
    scanf("%d",&a[i]);
    update(i,a[i]);    
    }
    
    for(int j=1;j<=m;j++)
    {
        int x,y;
        scanf("%d%d%d",&b,&x,&y);
        if(b==1)
            update(x,y);
        else
           printf("%d
",query(y)-query(x-1));    
    }
    return 0;
}