回顾树状数组

Posted 2020-09-29 阿波罗2003

　　树状数组是一种常用的数据结构，能够在O(log₂n)的时间内进行单点修改和求前缀和。因为代码量小、常熟小往往在某些应用中快于线段树(当然有些问题是不能呢用树状数组完成的)。

最基本的树状数组

　　方法1:用一个数组，O(1)修改, O(n)查询

　　方法2:求前缀和，O(n)修改，O(1)查询

　　以上两种方法卡一卡就TLE了。

　　树状数组就平衡了一下这两种方法，修改的时候多修改一点，查询的时候多算一点。

　　为了清楚地明白树状数组是如何运作的，我们实现定义 lowbit(x) 是写成2进制后的x中最后一位1。例如(10)₁₀ = (1010)₂，则lowbit(10) = (10)₂ = (2)₁₀.

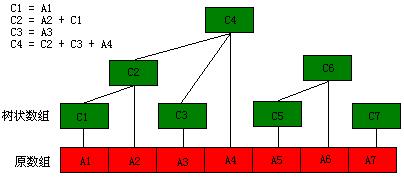
　　树状数组本质上就是一个长度为n的数组，但是它的每一个位置管辖另一些位置(就是它们的和)，对于一个节点i，它的数据同时会被加在节点(i + lowbit(i))上。例如下面这幅图。

　　至于计算这个lowbit通常是用这么一个快捷的方法:

1 #define lowbit(x) ((x) & (-x))

　　对于修改操作，就不断去更新管辖当前节点的节点，直到超出范围。

1 inline void add(int idx, LL val) {
2     for(; idx <= s; idx += lowbit(idx))
3         a[idx] += val;
4 }

　　现在证明修改操作是O(log₂n)的。

　　1) 当 idx 写成2进制后，1的个数不为1时，每次 idx += lowbit(idx) 时，至少有1个1进位，显然至多log₂idx次这样的操作idx写成二进制后就只有1个1了（1　　　　的个数只会减少不会增加）

　　2) 当 idx 写成2进制后，1的个数为1时，显然lowbit(idx) = idx，所以每次加倍，但是又不能超过n，最多进行log₂n次这样的操作。

　　所以修改操作的时间复杂度时O(log₂n)。

　　观察上面，可以发现一个有趣的结论，树状数组的一个节点i存的值，恰好是原数组中lowbit(i)个连续的元素和的和。

　　所以求前缀和的操作，就向前依次去加它没有算到的原数组的数(不是暴力，是直接加树状数组中节点的值)

1 inline LL getSum(int idx) {
2     LL rt = 0;
3     for(; idx; idx -= lowbit(idx))
4         rt += a[idx];
5     return rt;
6 }

　　对于求任意一段区间的和就前缀和减减就好了。

各种乱搞的树状数组

支持区间修改单点查询的树状数组

　　这个似乎不是树状数组的本职工作，但还是可以做的。

　　差分是一个离线的"算法"吧，能够支持O(1)修改，O(n)查询(但是只能在最后查询)。

　　差分数组满足一个性质，就是位置i的前缀和是在它真正的值。(差分数组秋求前缀和后得到的是原数组)

　　不懂差分数组的就看张图吧:

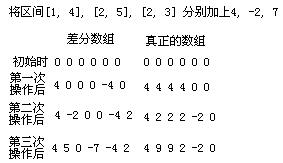
　　（差分数组的前缀和就是原数组）

　　既然差分数组能够快速地进行区间修改(本质上时单点修改)，求单点是靠求前缀和实现。而树状数组支持单点修改和快速求前缀和，于是用树状数组维护差分数组就能快速做到单点查询和区间修改。

支持区间修改区间查询的树状数组

　　也许你认为线段树可以完成，但是对于这种水题不想出动线段树(懒得写)，这时就可以考虑一下树状数组。

　　树状数组可以优秀地利用差分来求单点，所以先考虑暴力用差分求前缀和(考虑差分数组每个位置被计算的次数)。

　　

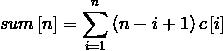
　　这个还可以化简原式。然后发现这两个都可以用树状数组维护，然后对于任意区间减一减就好了。

Code

  1 /**
  2  * Codevs
  3  * Problem#1082
  4  * Accepted
  5  * Time:430ms
  6  * Memory:11240k
  7  */
  8 #include <iostream>
  9 #include <cstdio>
 10 #include <ctime>
 11 #include <cmath>
 12 #include <cctype>
 13 #include <cstring>
 14 #include <cstdlib>
 15 #include <fstream>
 16 #include <sstream>
 17 #include <algorithm>
 18 #include <map>
 19 #include <set>
 20 #include <stack>
 21 #include <queue>
 22 #include <vector>
 23 #include <stack>
 24 #ifndef WIN32
 25 #define Auto "%lld"
 26 #else
 27 #define Auto "%I64d"
 28 #endif
 29 using namespace std;
 30 typedef bool boolean;
 31 const signed int inf = (signed)((1u << 31) - 1);
 32 const signed long long llf = (signed long long)((1ull << 63) - 1);
 33 const double eps = 1e-6;
 34 const int binary_limit = 128;
 35 #define smin(a, b) a = min(a, b)
 36 #define smax(a, b) a = max(a, b)
 37 #define max3(a, b, c) max(a, max(b, c))
 38 #define min3(a, b, c) min(a, min(b, c))
 39 template<typename T>
 40 inline boolean readInteger(T& u){
 41     char x;
 42     int aFlag = 1;
 43     while(!isdigit((x = getchar())) && x != \'-\' && x != -1);
 44     if(x == -1) {
 45         ungetc(x, stdin);    
 46         return false;
 47     }
 48     if(x == \'-\'){
 49         x = getchar();
 50         aFlag = -1;
 51     }
 52     for(u = x - \'0\'; isdigit((x = getchar())); u = (u * 10) + x - \'0\');
 53     ungetc(x, stdin);
 54     u *= aFlag;
 55     return true;
 56 }
 57 
 58 #define LL long long
 59 #define lowbit(x) (x & (-x))
 60 
 61 typedef class IndexedTree {
 62     public:
 63         LL* a;
 64         int s;
 65         IndexedTree():a(NULL), s(0) {        }
 66         IndexedTree(int n):s(n) {
 67             a = new LL[(n + 1)];
 68             memset(a, 0, sizeof(LL) * (n + 1));
 69         }
 70         
 71         inline void add(int idx, LL val) {
 72             for(; idx <= s; idx += lowbit(idx))
 73                 a[idx] += val;
 74         }
 75         
 76         inline LL getSum(int idx) {
 77             LL rt = 0;
 78             for(; idx; idx -= lowbit(idx))
 79                 rt += a[idx];
 80             return rt;
 81         }
 82 }IndexedTree;
 83 
 84 typedef class SegmentableIndexedTree {
 85     public:
 86         LL *a;
 87         LL *ps;                    // prefix sum
 88         IndexedTree s;            // sum
 89         IndexedTree us;            // unique sum
 90         
 91         SegmentableIndexedTree():a(NULL) {        }
 92         SegmentableIndexedTree(int n, LL *a):a(a) {
 93             s = IndexedTree(n + 1);
 94             us = IndexedTree(n + 1);
 95             ps = new LL[(n + 1)];
 96             ps[0] = 0;
 97             for(int i = 1; i <= n; i++)
 98                 ps[i] = ps[i - 1] + a[i];
 99         }
100         
101         inline void add(int l, int r, LL val) {
102             s.add(l, val), us.add(l, l * val);
103             s.add(r + 1, -val), us.add(r + 1, -(r + 1) * val);
104         }
105         
106         inline LL getSum(int idx) {
107             return (idx + 1) * s.getSum(idx) - us.getSum(idx);
108         }
109         
110         inline LL getSum(int l, int r) {
111             return ps[r] - ps[l - 1] + getSum(r) - getSum(l - 1);
112         }
113 }SegmentableIndexedTree;
114 
115 int n, m;
116 LL *a;
117 SegmentableIndexedTree sit;
118 
119 inline void init() {
120     readInteger(n);
121     a = new LL[(n + 1)];
122     for(int i = 1; i <= n; i++)
123         readInteger(a[i]);
124 }
125 
126 inline void solve() {
127     int opt, l, r, x;
128     sit = SegmentableIndexedTree(n, a);
129     readInteger(m);
130     while(m--) {
131         readInteger(opt);
132         readInteger(l);
133         readInteger(r);
134         if(opt == 1) {
135             readInteger(x);
136             sit.add(l, r, x);
137         } else {
138             printf(Auto"\\n", sit.getSum(l, r));
139         }
140     }
141 }
142 
143 int main() {
144     init();
145     solve();
146     return 0;
147 }