矩阵连乘问题_动态规划
Posted henuliulei
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵连乘问题_动态规划相关的知识,希望对你有一定的参考价值。
1)问题引导




从上面我们可以知道不同的结合方式,矩阵计算的次序数不一样,那么如何求这个最小次序数的划分,即如何结合。这就是矩阵连乘问题
使用动态规划可以解决





如下图,如果我们使用递归,则会产生大量的重复计算,复杂度太高,当然使用备忘录降低复杂度。不过更好的是使用递推
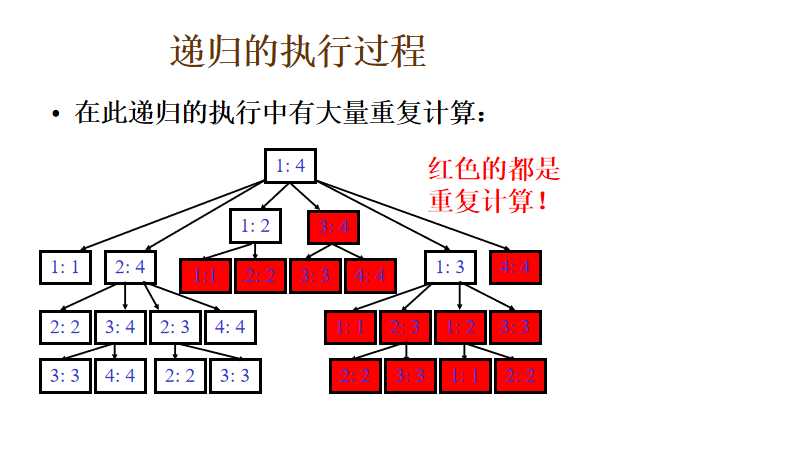
递推算法分析如下:


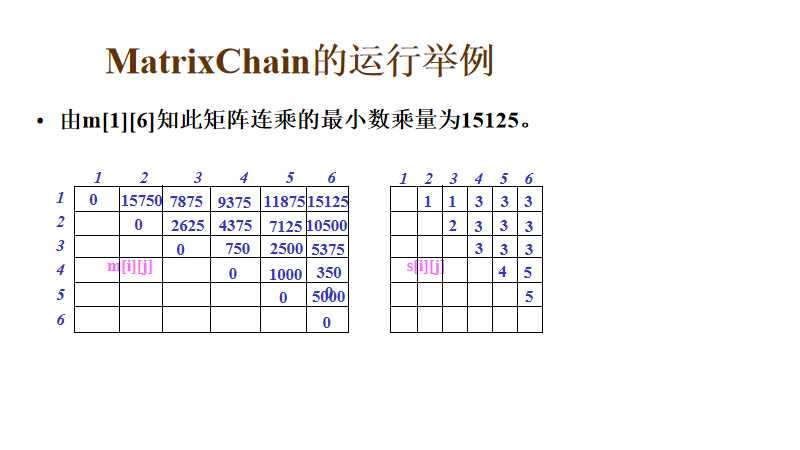
1 #include<bits/stdc++.h> 2 using namespace std; 3 void matrixChain(int n,int p[],int m[][100],int s[][100])//递推 4 { 5 for(int i=1;i<=n;i++){//对角线先为0 6 m[i][i]=0; 7 } 8 for(int r=2;r<=n;r++){//一共n-1个对角线 9 for(int i=1;i<=n-r+1;i++){//第i行 10 int j=i+r-1;//在该行的对角线上的点对应的j值 11 m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];//初始化此时在i处取得最优解 12 s[i][j]=i; 13 for(int k=i+1;k<j;k++){//如果有更小的则被替换 14 int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]; 15 if(t<m[i][j]) 16 { 17 m[i][j]=t; 18 s[i][j]=k; 19 } 20 } 21 } 22 } 23 } 24 void print_optimal_parents(int s[100][100],int i,int j)//打印划分的结果 25 { 26 if( i == j) 27 cout<<"A"<<i; 28 else 29 { 30 cout<<"("; 31 print_optimal_parents(s,i,s[i][j]); 32 print_optimal_parents(s,s[i][j]+1,j); 33 cout<<")"; 34 } 35 36 } 37 int main() 38 { 39 int p[1000];//每个矩阵的行数和最后一个的列数 40 int m[100][100];//存储最优子结构 41 int s[100][100];//存储当前结构的最优断点 42 memset(p,0,sizeof(p)); 43 memset(m,0,sizeof(m)); 44 memset(s,0,sizeof(s)); 45 cout << "请输入矩阵的个数"<< endl; 46 int n; 47 cin >> n; 48 cout << "请依次输入每个矩阵的行数和最后一个矩阵的列数"<< endl; 49 for(int i=0;i<=n;i++){ 50 cin >> p[i]; 51 } 52 matrixChain(n,p,m,s); 53 cout <<"这些矩阵相乘的最少次数是"<<m[1][n]<<endl; 54 55 cout<<"结果是:"<<endl; 56 print_optimal_parents(s,1,n); 57 return 0; 58 }
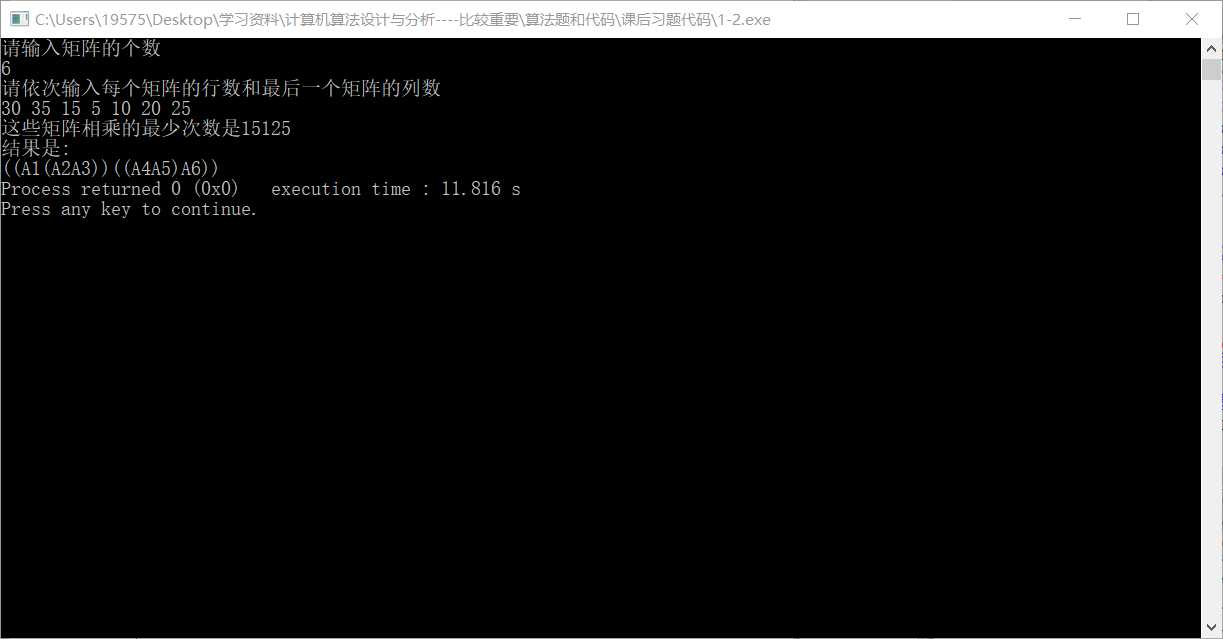
以上是关于矩阵连乘问题_动态规划的主要内容,如果未能解决你的问题,请参考以下文章