动态规划之矩阵连乘

Posted 2021-04-18 AI小白奋斗史

零.描述

题目：给定n个矩阵{A0,A1,A2, …, An-1}，其中Ai，i=0, …, n-1的维数为 pi*pi+1，并且 Ai和 Ai+1是可乘的。考察这 n 个矩阵的连乘积 A0A1A2…An-1，由于矩阵乘法满足结合律，所以计算矩阵的连乘可以有多种不同的计算次序。结合动态规划思想，编程确定 n 个矩阵的连乘次序，使得按照这个次数计算矩阵连乘，需要的“数乘”次数最少。

Input：输入矩阵个数 n，以及每一个矩阵的尺寸；

Output：输出最佳矩阵连乘次序和数乘次数；

比如

A0[20*25]，A1[25*15]，A2[15*5]，A3[5*12]

则结果可能有以下情况

(A0A1)(A2A3)、((A0(A1A2))A3)、A0((A1A2)A3)...

我们需要得到计算效率最优的括号方式

---

二.算法：动态规划

原问题为n个矩阵连乘，利用动态规划的思想将原问题分解为子问题，

(1) n==1时，单一矩阵，不需要计算，最小数乘次数为0；

(2) n==2时，根据n==1时的结果，遍历计算出每相邻两个矩阵的最小乘次；

(3) n==3时，根据n==1和n==2时的结果，此时已经求出每相邻1个，2个矩阵的最小乘次，遍历计算出该相邻三个矩阵的最小乘次；

以此类推，当n==k时，根据n==1,n==2,n==k-1时的结果，此时已经求出每相邻1个，2个，3个......k-1个矩阵的最小乘次。每当n增加1时，就利用已求出的子结构来求解此时的最优解。

动态规划步骤：

(1) 定义子问题。DP[i,j]表示从第i个矩阵到第j个矩阵，可通过DP得到优化解。

(2) 建立子问题之间的关系。

设矩阵Ai的维数为Pi*Pi+1，DP[i,j]表示得到Ai,j的最小相乘次数，递推方程如下：

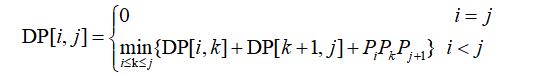
(3) 确定边界条件。当i=j，只有一个矩阵，DP[i,j]=0

(4) 得到原问题的解

对于具体例子

A = [20*25,25*15,15*5,5*12]，按照递推方程可以得到以下结果

注意：计算顺序为先计算红色区域，再计算蓝色区域，最后计算黄色区域。分别代表两个矩阵连乘、三个矩阵连乘和四个矩阵连乘。

---

三.编程实现

import numpy as np

def matrixChain(p, n=1, memo=None, seq=None):
    size = len(p) - n  # 子问题个数
    if n == 1:  # 长度为1的矩阵链，数乘次数为0
        memo = np.zeros([size, size], dtype=int)
        seq = np.zeros([size, size], dtype=int)
    else:
        for i in range(size):  # 左边界
            j = i + n - 1  # 右边界
            for k in range(i, j):  # 分界位置
                t = memo[i, k] + memo[k + 1, j] + p[i] * p[k + 1] * p[j + 1]
                if t < memo[i, j] or memo[i, j] == 0:
                    memo[i, j] = t
                    seq[i, j] = k
    if n < len(p) - 1:
        matrixChain(p, n + 1, memo, seq)
    return memo, seq


def prtSeq(seq, i, j):
    size = j - i + 1
    if size == 1:
        return 'A%d' % i  # A1,A2..
    else:
        k = seq[i, j]  # 分界位置
        res = ''
        res += '(' + prtSeq(seq, i, k)
        res += prtSeq(seq, k + 1, j) + ')'
        return res


if __name__ == '__main__':
    n = eval(input('请输入矩阵个数：'))  # 4
    p = eval(input('请输入矩阵尺寸：'))  # 20,25,15,5,12
    m, seq = matrixChain(p)
    res = prtSeq(seq, 0, n - 1)
    print('最佳数乘次序：%s, 此时数乘次数：%d' % (res[1:-1], m[0, -1]))
    # 最佳数乘次序：(A0(A1A2))A3, 此时数乘次数：5575

---

END

往期回顾