矩阵连乘最优解---动态规划
Posted 茶飘香~
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵连乘最优解---动态规划相关的知识,希望对你有一定的参考价值。
代码如下:
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> #include <map> #define N 1000005 using namespace std; int p[1005],s[1005][1005],dp[1005][1005]; void print(int i,int j) { if(i==j) { cout<<"A"<<i; return ; } int k=s[i][j]; if(i==k) cout<<"A"<<i; else if(i<k-1) { cout<<"("; print(i,k); cout<<")"; } else if(i==k-1) cout<<"(A"<<i<<"A"<<k<<")"; if(k+1==j) cout<<"A"<<k+1; else if(k+1<j-1) { cout<<"("; print(k+1,j); cout<<")"; } else if(k+1==j-1) cout<<"(A"<<k+1<<"A"<<j<<")"; } int main() { int n; printf("input matrix number:"); scanf("%d",&n); for(int i=0; i<=n; i++) scanf("%d",&p[i]); memset(dp,0,sizeof(dp)); for(int len=1; len<n; len++) { for(int i=1; i+len<=n; i++) { dp[i][i+len]=dp[i+1][i+len]+p[i-1]*p[i]*p[i+len]; s[i][i+len]=i; for(int k=i+1; k<i+len; k++) { int t=dp[i][k]+dp[k+1][i+len]+p[i-1]*p[k]*p[i+len]; if(dp[i][i+len]>t) { dp[i][i+len]=t; s[i][i+len]=k; } } } } for(int i=1; i<=n; i++) { for(int j=1; j<=n; j++) { if(j<i) printf(" "); else printf("%6d",dp[i][j]); } cout<<endl; } cout<<"answer: "; cout<<"("; print(1,n); cout<<")"<<endl; return 0; }
运行截图:
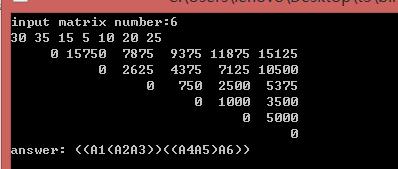
以上是关于矩阵连乘最优解---动态规划的主要内容,如果未能解决你的问题,请参考以下文章