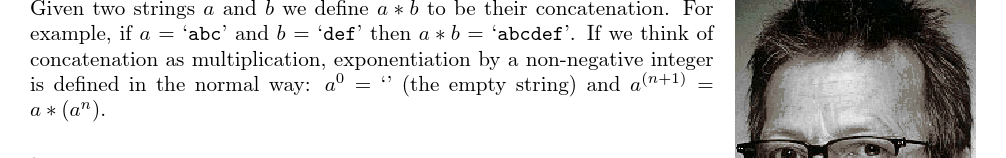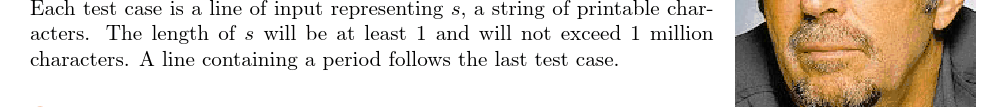「UVA10298」 Power Strings（KMP

Posted 2021-01-13 qwerta

题目描述

PDF

输入输出格式

输入格式：

输出格式：

输入输出样例

输入样例#1： 复制

abcd
aaaa
ababab
.

输出样例#1： 复制

1
4
3

题解

Luogu的题解

这里是对目前最高赞题解结论的证明。

结论：设字符串长度为$n$，最长相同前后缀的长度为$next[i]$，

如$n$%$(n-next[n])=0$，则答案为$n/(n-next[n])$，否则为$1$。

证明：

我们求$next$数组的时候，相当于每次把当前串这样对齐了一下↓

而$next$求到$n$时，上面串的$n$对应的就是下面串的$next[n]$。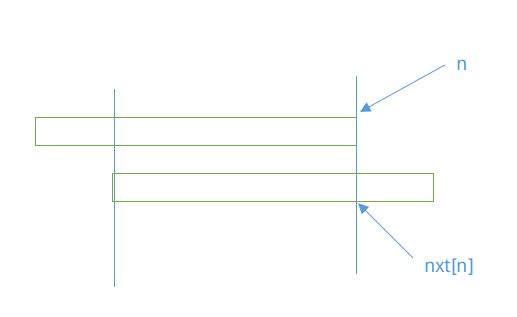

这时候的$n-nxt[n]$就是箭头指向的绿色部分。

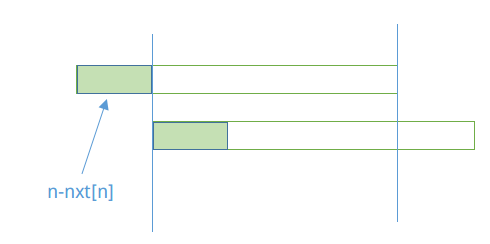
而上下两串其实是一样的，所以下面串的前$n-nxt[n]$格和上面串的前$n-nxt[n]$相同。

又因为两串由蓝色框住的部分匹配，所以下面的绿框对应的部分和绿框相同。

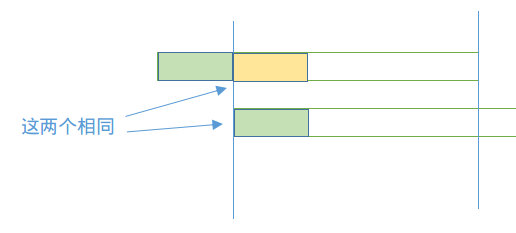
依此递推，可以得到，**如果循环节多于一个**，以前$n-nxt[n]$个为循环节，是可以铺满整串的。而且因为$nxt[n]$是尽量大的，所以这样得到的循环节长度为所有可能情况中最小的，也就是我们所求的。

而如果$n$%$(n-next[n])≠0$，可以认为之前的循环节匹配仍然可以进行，但是最后一个循环节被强行割掉了一些。

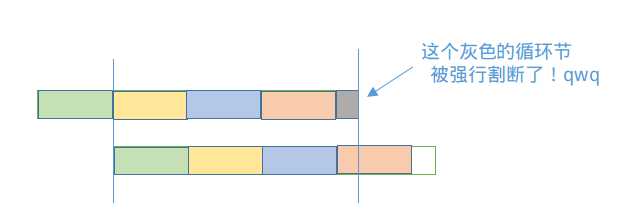
显然这样就怎么都安排不上了。

所以如$n$%$(n-next[n])=0$，就能排上，答案为$n/(n-next[n])$，否则只能以自己为循环节，答案为$1$。

代码实现的时候注意一下自己代码中$n$的定义和$nxt$数组的定义什么的。

还是放一下我的代码叭qwq

 1 /*
 2     qwerta
 3     UVA10298 Power Strings
 4     Accepted
 5     代码 C++，0.65KB
 6     提交时间 2018-10-12 17:59:53
 7     耗时/内存
 8     100ms, 0KB
 9 */
10 #include<iostream>
11 #include<cstdio>
12 using namespace std;
13 int nxt[1000003];
14 int main()
15 {
16     //freopen("a.in","r",stdin);
17     while(1)
18     {
19         string s;
20         getline(cin,s);//读入一整行，放进s
21         if(s.length()==1&&s[0]==‘.‘)break;
22         int lens=s.length();
23         //kmp求next
24         int k=-1;
25         nxt[0]=-1;
26         for(register int i=1;i<lens;++i)
27         {
28             while(k!=-1&&s[i]!=s[k+1])k=nxt[k];
29             if(s[i]==s[k+1])k++;
30             nxt[i]=k;
31         }
32         int n=lens-1;
33         if((n+1)%(n-nxt[n])==0)//如果能恰好排满循环节
34         printf("%d
",((n+1)/(n-nxt[n])));//输出总长除以循环节长度
35         else printf("1
");//否则输出1
36     }
37     return 0;
38 }

吐槽：拿来做模拟题压轴被吐槽是结论题......

明明前两天才讲过啊！（摔