平时九测

Posted 2021-01-10 edsheeran

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了平时九测相关的知识，希望对你有一定的参考价值。

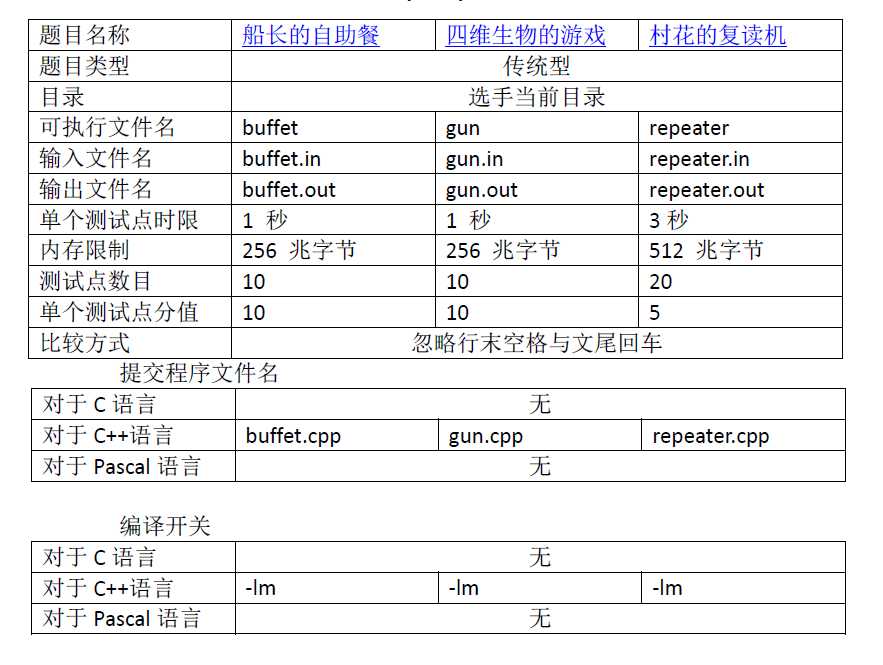
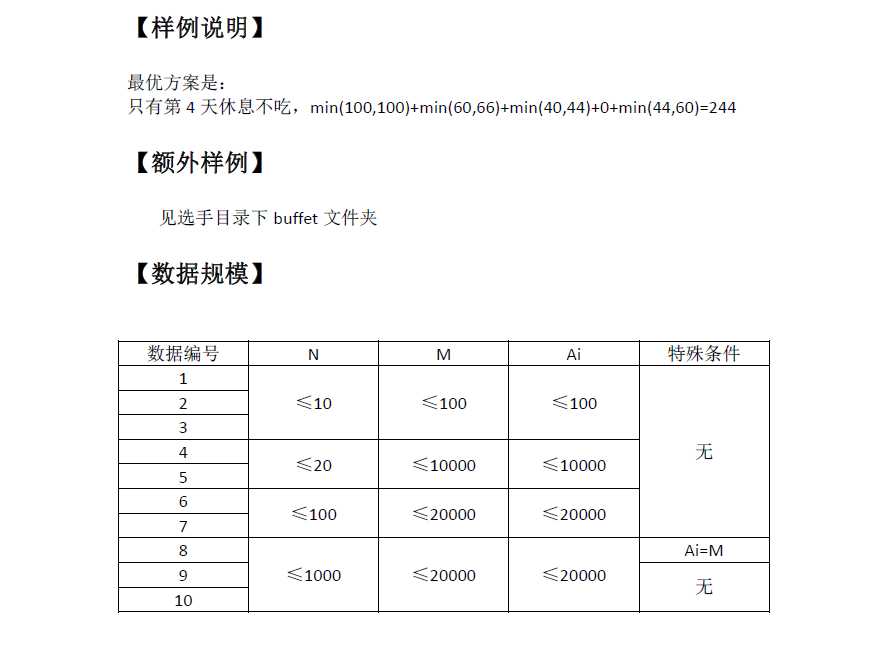
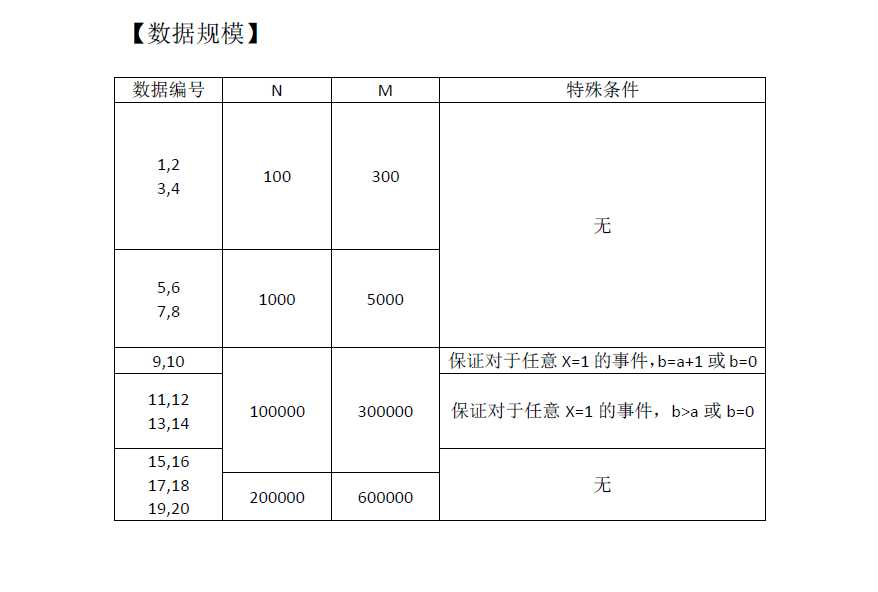
技术分享图片

题解：

第一题：简单DP, 首先容量会是固定的最多Ｎ个数，所以复杂度是Ｎ＾２的；

先预处理各个容量的等级，dp[ i ][ j ][ 0/1 ] 表示考虑第i个菜时此时容量的等级为j， 0表示上一次没吃， 1表示上一次吃了，然后枚举这次吃没有吃往后刷就可以了；

#include<bits/stdc++.h>
using namespace std;
const int M = 1005;
int ap[M], d[M], dp[M][M][2];
inline void up(int &a, int b){
    if(b > a) a = b;
}
int main(){
    freopen("buffet.in","r",stdin);
    freopen("buffet.out","w",stdout);
    int n, inf = -2e9;
    scanf("%d%d", &n, &ap[1]);
    for(int i = 2; i <= n; i++) ap[i] = ap[i-1]*2/3;
    for(int i = 1; i <= n; i++) scanf("%d", &d[i]);
    memset(dp, 0x8f, sizeof(dp));
    dp[1][1][0] = 0;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++){
            if(dp[i][j][0] > inf){
                up(dp[i+1][j+1][1], dp[i][j][0] + min(ap[j], d[i]));
                up(dp[i+1][1][0], dp[i][j][0]);
            }
            if(dp[i][j][1] > inf){
                up(dp[i+1][j+1][1], dp[i][j][1] + min(ap[j], d[i]));
                up(dp[i+1][j-1][0], dp[i][j][1]);
            }
            //printf("%d %d %d %d
",i, ap[j], dp[i][j][0], dp[i][j][1]);
        }
    int ret = 0;
    for(int i = 1; i <= n; i++)ret = max(ret, max(dp[n+1][i][0], dp[n+1][i][1]));
    printf("%d
", ret);
}

View Code

第二题：日常%%% yl大佬，太聪明了；

概率DP，dp[res][pos]表示还剩下res个人，在这res个人中相对编号为pos，在1拿着手枪时的获胜概率；p表示1这一枪有子弹的概率；

第一种情况，1打死了右边的0号，那么抢传到了左边的2号，此时剩余res-1个人，每个人的相对编号-1；贡献就是p * dp[res-1][pos-1];

第二种情况，如果这枪没有子弹，他就会传给右边的k个人，每个人的相对编号减小，pos就变成了(pos - k% res + res) % res;

所以 dp[res][pos] = dp[res - 1][pos - 1] * p + (1 -p) * dp[res][(pos - k% res + res) % res]；

第一个dp可以交给下一层解决，第二个dp一直往下扩展就会回到当前状态（相当于手枪又传回来了）；

我们把第二个dp展开，用?表示第一个dp，用D表示第二个dp; 那么他就等价于 p1*? + ( (1-p1) * ( p2 *? + (1 - p2) * (p3 * ? +…… * （pn* ? + (1-pn) *dp[res][pos) ) ) + (1 -p3) * D ) ),

即dp[res][pos] = 一堆? + 一堆系数*dp[res][pos]；所以我们可以先处理出前面一堆? ，后面的直接往下搜，搜到终点（也是起点，即一圈完了）就可以得到dp值，在一步步返回更新；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 1005;
ll dp[M][M];
bool vis[M][M];
int N, C, K, ni;
const ll mod = 1e9 + 9;
ll ksm(ll a, int b){
    ll ret = 1;
    for( ; b; b>>=1, a=a*a%mod)
        if(b&1) ret=ret*a%mod;
    return ret; 
}


ll dfs(int res, int pos, ll gx, ll gl){//res, pos意思同上，gx就是那一推可以交给下一层的东西，gl就是那一堆系数 
    if(pos == -1) return 0;//如果pos==-1,说明这个人死了 
    if(res == 1) return 1;//如果他是剩下的一个人，他就赢了 
    if(vis[res][pos] && dp[res][pos] == -1){//一圈走完回到起点可以直接算出dp值 
        dp[res][pos] = gx * ksm(1 - gl + mod, mod - 2) % mod;
        return dp[res][pos];
    }
    if(vis[res][pos]) return dp[res][pos];
    vis[res][pos] = 1;
    dfs(res, (pos - K % res + res) % res, (gx + ( 1LL * (res - 1) * ni % mod * gl % mod * dfs(res - 1, pos - 1, 0, 1) ) % mod) % mod, 1LL * gl * (C - res + 1) % mod * ni % mod);
    //处理出gx,gl； 
    if(dp[res][pos] != -1) return dp[res][pos];//如果这个点是起点，他就已经被更新过，不用管 
    dp[res][pos] =  1LL * (res - 1) * ni % mod * dfs(res - 1, pos - 1, 0, 1) % mod + 1LL * (C - res + 1) * ni % mod * dp[res][(pos - K % res + res) % res] % mod;
    dp[res][pos] %= mod;//没有更新过，就按dp方程更新 
    return dp[res][pos];
}


int main(){
    freopen("gun.in","r",stdin);
    freopen("gun.out","w",stdout);
    int T;
    scanf("%d", &T);
    while(T--){
        scanf("%d%d%d", &N, &C, &K);
        memset(dp, -1, sizeof(dp));
        memset(vis, 0, sizeof(vis));
        ni = ksm(C, mod - 2);
        for(int i = 0; i < N; i++){
            ll ret = dfs(N, i, 0, 1);
            printf("%lld ", ret);
        }
        puts("");        
    }
}

第三题：LCT；以下是std

20分算法（11,12,13,14）
?不难发现，这种数据有一个明显的特征：不会形成环。
?那么这个问题就变为：可以更改一个点的父亲节点，然后询问b是否为a的祖先。
?可以考虑维护DFN序，迚入X的子树的位置设为Xl,离开X的子树的位置设为Xr；对于每个询问，只需要查询al是否在bl和br间即可。这可以通过统计在al,bl,br左侧的点的总数来判断。
?这些都可以通过平衡树维护区间完成。

其实100分算法就是上面那个算法的延伸
?如果存在环，问题就变得有些麻烦了。
?但由于这是一颗基环内向树，我们可以特殊维护环上的一条边。
?换言，可以维护根节点的“父亲“，但这一父子关系并没有在平衡树中体现。而是单独使用一个数组存储。

这样一来，对于每次询问，首先查询b是否为a的祖先，如果当前的根节点有一个“父亲”，那么检查a是否为“父亲”的祖先。
?这两个问题只要有一个为真，则说明a能到达b

对于修改操作，我们拆分为两步：
?断开a到它原来的父亲fa
?链接a到它新的父亲b

断开操作：
?如果a就是根，那直接将其“父亲”设为0即可
?否则，
?如果a的根节点没有“父亲”
?那么就是一棵树，直接操作即可。
?如果a的根节点（设为x）有“父亲”（设为y），那么如果a为y的祖先，则说明a,x,y在基环中，可以先像树一样，断开a到其父亲的边，然后将x连到y下面。此时a就是这棵树的根了，和上面的操作一样，将a的“父亲”设为0即可。

链接操作（此时a是它所在的子树的根）：
?如果a是b的祖先，那么将a的“父亲”设为b.
?如果a丌是b的祖先，那么直接向树一样连边即可。
?于是就可以过了，时间复杂度O(nlogn)

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<assert.h>
#define SF scanf
#define PF printf
#define MAXN 200010
#define MOD 1000000009
using namespace std;
typedef long long ll;
struct node *NIL;
struct node{
    node *ch[2],*fa;
    int val,siz;
    bool Dir(){
        return this==fa->ch[1];
    }
    void setchild(node *x,int d){
        ch[d]=x;
        if(x!=NIL)
            x->fa=this;
    }
    void pushup(){
        siz=ch[0]->siz+ch[1]->siz+1;
    }
}tree[MAXN*2];
int fax[MAXN];
node *lc[MAXN],*rc[MAXN];
node * Newnode(node *x,int val){
    x->ch[0]=x->ch[1]=x->fa=NIL;
    x->val=val;
    x->siz=1;
    return x;
}
void Rotate(node *x){
    node *y=x->fa;
    int d=x->Dir();
    if(y->fa==NIL)
        x->fa=NIL;
    else
        y->fa->setchild(x,y->Dir());
    y->setchild(x->ch[!d],d);
    x->setchild(y,!d);
    y->pushup();
}
void Splay(node *x,node *rt){
    while(x->fa!=rt){
        node *y=x->fa;
        if(y->fa==rt){
            Rotate(x);
            break;
        }
        if(x->Dir()==y->Dir())
            Rotate(y);
        else
            Rotate(x);
        Rotate(x);
    }
    x->pushup();
}
node *find_nxt(node *x,int d){
    while(x->ch[d]!=NIL)
        x=x->ch[d];
    return x;    
}
int check(int a,int b){
    Splay(lc[a],NIL);
    node *rta=find_nxt(lc[a],0);
    Splay(rta,NIL);
    
    Splay(lc[b],NIL);
    node *rtb=find_nxt(lc[b],0);
    Splay(rtb,NIL);
    
    if(rta!=rtb)
        return 0;
    
    Splay(lc[a],NIL);
    int siz1=lc[a]->ch[0]->siz;
    Splay(rc[a],NIL);
    int siz2=rc[a]->ch[0]->siz;
    Splay(lc[b],NIL);
    int siz=lc[b]->ch[0]->siz;
    if(siz1<siz&&siz<siz2)
        return 1;
    if(fax[rta->val]!=0){
        node *x=lc[fax[rta->val]];
        Splay(x,NIL);
        int sizx=x->ch[0]->siz;
        if(siz1<=sizx&&sizx<=siz2)
            return 1;    
    }
    return 0;
}
void cut(int x){
    node *a=lc[x];
    node *b=rc[x];
    Splay(a,NIL);
    if(a->ch[0]==NIL){
        fax[x]=0;
        return ;
    }
    node *rt=find_nxt(a,0);
    Splay(rt,NIL);
    if(fax[rt->val]==0||check(x,fax[rt->val])==0){
        Splay(rt,NIL);
        Splay(a,rt);
        Splay(b,a);
        node *t=find_nxt(b->ch[1],0);
        Splay(t,b);
        rt->setchild(t,1);
        t->setchild(a->ch[0],0);
        a->fa=NIL;
        a->ch[0]=NIL;
        b->ch[1]=NIL;
        t->pushup();
        rt->pushup();
        b->pushup();
        a->pushup();//cut a from x
    }
    else{
        node *c=lc[fax[rt->val]];
        fax[rt->val]=0;
        assert(rt->ch[0]==NIL);
        Splay(rt,NIL);
        Splay(a,rt);
        Splay(b,a);
        node *t=find_nxt(b->ch[1],0);
        Splay(t,b);
        rt->setchild(t,1);
        t->setchild(a->ch[0],0);
        a->fa=NIL;
        a->ch[0]=NIL;
        b->ch[1]=NIL;
        t->pushup();
        rt->pushup();
        b->pushup();
        a->pushup();//cut a from x
        
        //PF("{%d %d}
",a->ch[0]-tree,a->ch[1]-tree);
        
        Splay(c,NIL);
        node *d=find_nxt(c->ch[1],0);
        Splay(d,c);
        d->setchild(rt,0);
        d->pushup();
        c->pushup();
    }
}
void link(int a,int b){
    Splay(lc[a],NIL);
    assert(lc[a]->ch[0]==NIL);
    if(check(a,b)||a==b){//we can reach a from b
        fax[a]=b;
    }
    else{
        Splay(lc[a],NIL);
        node *c=lc[b];
        Splay(c,NIL);
        node *d=find_nxt(c->ch[1],0);
        Splay(d,c);
        d->setchild(lc[a],0);
        d->pushup();
        c->pushup();
    }
}
int n,m;
int main(){
    freopen("repeater.in","r",stdin);
    freopen("repeater.out","w",stdout);
    int tag,a,b;
    NIL=&tree[0];
    NIL->ch[0]=NIL->ch[1]=NIL->fa=NIL;
    SF("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        lc[i]=Newnode(&tree[i],i);
        rc[i]=Newnode(&tree[i+n],i);
        lc[i]->setchild(rc[i],1);
    }
    ll ans=0;
    int cnt=0;
    for(int i=1;i<=m;i++){
        //PF("[now,begin %d]:
",i);
        SF("%d%d%d",&tag,&a,&b);    
        if(tag==1){
            cut(a);
            if(b!=0)
                link(a,b);
        }
        else{
            //PF("{%d}
",check(b,a));
            ans=(ans*2ll+check(b,a))%MOD;
        }
        /*for(int i=1;i<=n;i++){
            PF("fa:(%d)",fax[i]);
            PF("<%d,(%d),%d> | <%d,(%d),%d>
",lc[i]->ch[0]-tree,lc[i]-tree,lc[i]->ch[1]-tree,rc[i]->ch[0]-tree,rc[i]-tree,rc[i]->ch[1]-tree);    
        }*/
    }
    PF("%lld",ans);
}

View Code

以上是关于平时九测的主要内容，如果未能解决你的问题，请参考以下文章

暑假第九测

暑假第二十九测

VsCode 代码片段-提升研发效率

VSCode插件开发全攻略代码片段设置自定义欢迎页

在PaddlePaddle中的Notebook代码片段

译文：18个实用的JavaScript代码片段，助你快速处理日常编程任务