关于堆结构的详解

Posted 2021-01-06 sxkgeek

一、定义

堆的定义

堆其实就是一棵完全二叉树（若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边），

定义为：具有n个元素的序列（h1,h2,...hn），当且仅当满足（hi>=h2i,hi>=h2i+1）或（hi<=h2i,hi<=2i+1） (i=1,2,...,n/2)时称之为堆

大顶堆

堆顶元素（即第一个元素）为最大项，并且（hi>=h2i,hi>=h2i+1）

小顶堆

堆顶元素为最小项，并且（hi<=h2i,hi<=2i+1）

二、构建堆（大顶堆）

方法

序列对应一个完全二叉树，从最后一个分支节点（n div 2）开始，到跟（1）为止，一次对每个分支节点进行调整（下沉），以便形成以每个分支节点为根的堆，当最后对树根节点进行调整后，整个树就变成一个堆

实例

先给出一个序列：45，36，18，53，72，30，48，93，15，35

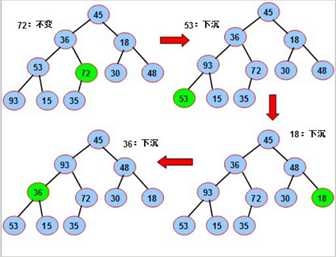
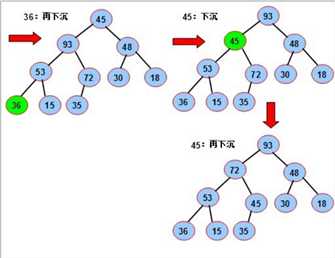
要想此序列称为一个堆，我们按照上述方法，首先从最后一个分支节点（10/2），其值为72开始，一次对每个分支节点53，18，36，45进行调整（下沉）

图解流程



代码实现

/*根据树的性质建堆，树节点前一半一定是分支节点，即有孩子的，所以我们从这里开始调整出初始堆*/    
 public static void adjust(List<Integer> heap){  
    for (int i = heap.size() / 2; i > 0; i--)    
        adjust(heap,i, heap.size()-1);    
        
    System.out.println("=================================================");  
    System.out.println("调整后的初始堆：");  
      print(heap);  
  }  
/**  
 * 调整堆，使其满足堆得定义  
 * @param i  
 * @param n  
 */    
public static void adjust(List<Integer> heap,int i, int n) {    
     
    int child;    
    for (; i <= n / 2; ) {    
        child = i * 2;    
        if(child+1<=n&&heap.get(child)<heap.get(child+1))    
            child+=1;/*使child指向值较大的孩子*/    
        if(heap.get(i)< heap.get(child)){    
            swap(heap,i, child);    
            /*交换后，以child为根的子树不一定满足堆定义，所以从child处开始调整*/    
            i = child;    
             
        }  else break;  
    }    
}   

//把list中的a,b位置的值互换   
public static void swap(List<Integer> heap, int a, int b) {   
    //临时存储child位置的值   
    int temp = (Integer) heap.get(a);   

    //把index的值赋给child的位置   
    heap.set(a, heap.get(b));   

    //把原来的child位置的数值赋值给index位置   
    heap.set(b, temp);   
}   

三、堆排序

堆排序的性能介绍（适合处理数据量大的序列）

由于它在直接选择排序的基础上利用了比较结果形成。效率提高很大。它完成排序的总比较次数为O(nlog2n)。

堆排序需要两个步骤，一个建堆，而是交换重新建堆。比较复杂，所以一般在小规模的序列中不合适，但对于较大的序列，将表现出优越的性能
　　

算法描述（建堆，交换重新建堆）：

• 初始时把要排序的数的序列看作是一棵顺序存储的二叉树，调整它们的存储序，使之成为一个 堆，这时堆的根节点的数最大
• 然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆
• 依此类推，直到只有两个节点的堆，并对 它们作交换，最后得到有n个节点的有序序列

代码实现

//对一个最大堆heap排序  
public static void heapSort(List<Integer> heap) {    
    
   for (int i = heap.size()-1; i > 0; i--) {    
    /*把根节点跟最后一个元素交换位置，调整剩下的n-1个节点，即可排好序*/    
       swap(heap,1, i);    
       adjust(heap,1, i - 1);    
   }    
}

四、堆排序的应用

场景：

如何从100万个数中找出最大的前100个数

算法分析：

先取出前100个数，维护一个100个数的最小堆，遍历一遍剩余的元素，在此过程中维护堆就可以了。

• 取前m个元素（例如m=100），建立一个小顶堆
• 顺序读取后续元素，直到结束。每次读取一个元素，如果该元素比堆顶元素小，直接丢弃
  如果大于堆顶元素，则用该元素替换堆顶元素，然后保持最小堆性质。
• 最后这个堆中的元素就是前最大的100个