数据结构堆及堆排序详解

Posted 2022-08-16 Kant101

1. 简介

堆（Heap）在计算机科学中可以表示内存的一部分，也是数据结构与算法中一种非常常用的数据结构。

尤其是在较大数据量的排序等问题中，堆排序经常被使用，因为堆排序的时间复杂度为 O(nlogn)。堆排序也是面试中经常被问到的对大量数据排序的算法，如海量数据选出 top K 等。

堆的结构
堆是一棵完全二叉树，且分为 大顶堆 和 小顶堆 两种结构：大顶堆中根结点的值大于左右子结点的值；小顶堆中根结点的值小于左右子结点的值。

大顶堆示例如下图所示：

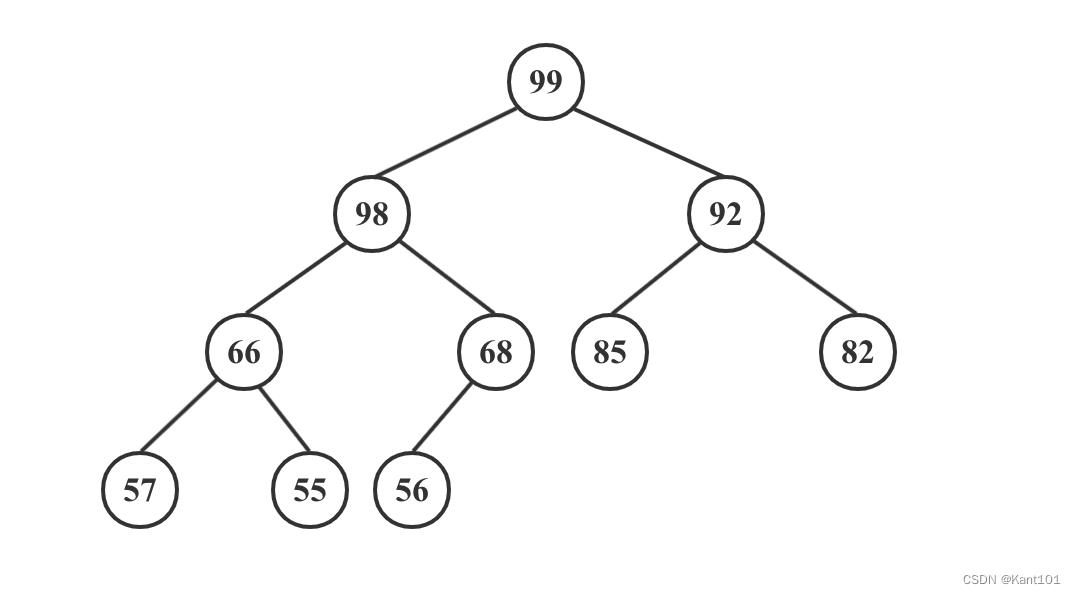
2. 建堆

我们以如下所示的原始完全二叉树为例，详细描述大顶堆建堆的整过程。

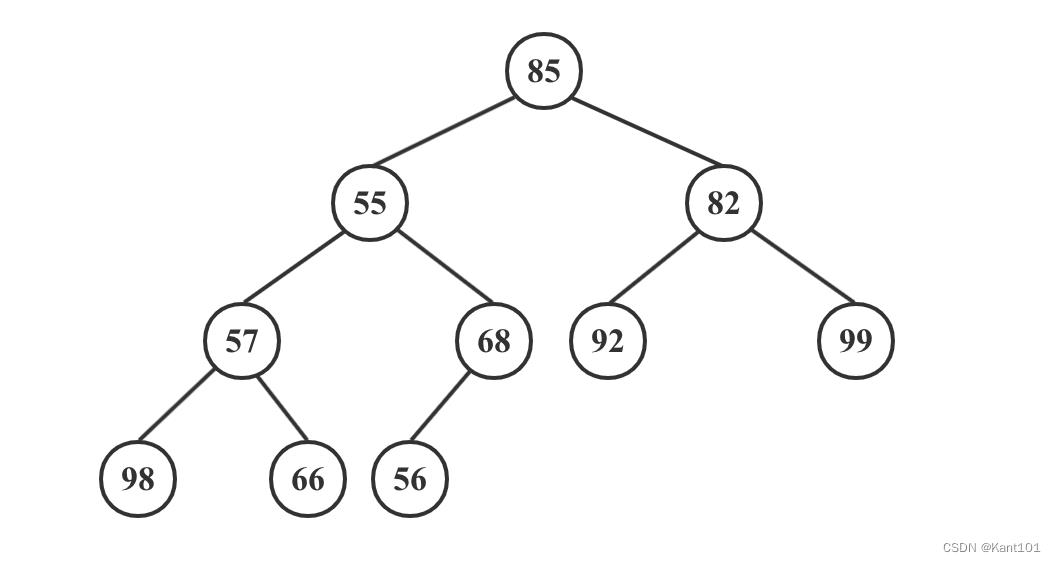
给定的数字的初始序列为: 85、55、82、57、68、92、99、98、66、56
将它们按照树的层序从上到下、从左到右依次摆放就得到如上图所示的初始的完全二叉树（堆是一种完全二叉树）

现在要调整这个初始堆，使它成为一个大顶堆。
调整的策略是：从最后一个结点开始从右向左、从下到上调增，使得父结点的值大于两个子结点的值。并且，对交换的子结点还要进行递归，使得它下面的子树仍然满足大顶堆的性质。

1）56比它的父结点68的值下，因此56不需要调整；

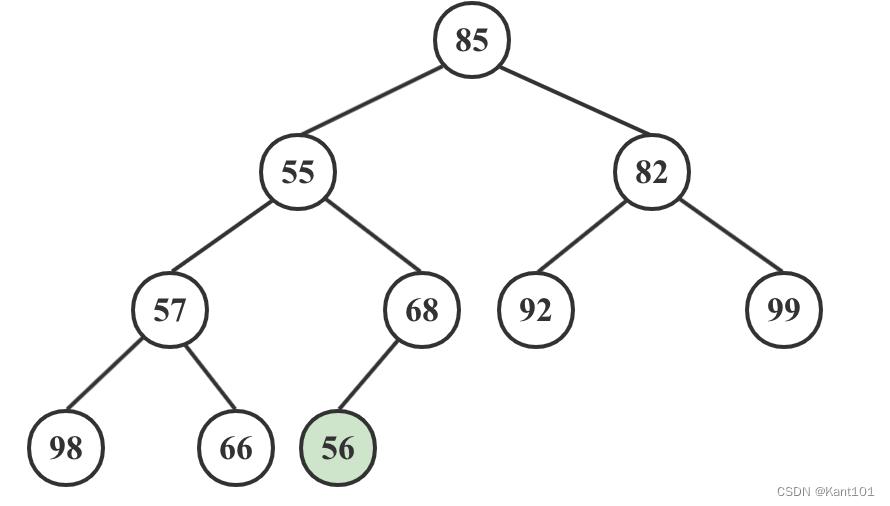
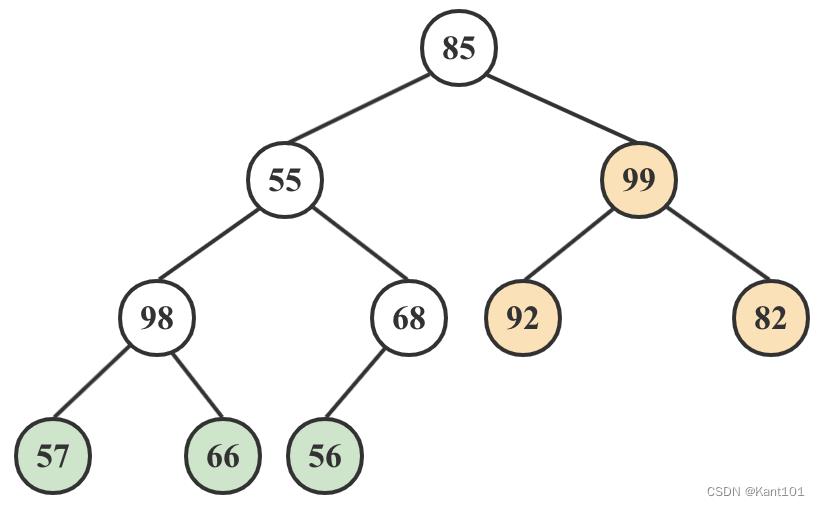
2）66和98两个子结点的值和它们的父结点相比较，选择最大的值做父结点，将原来的父结点的值与最大值的根结点交换，如下图：

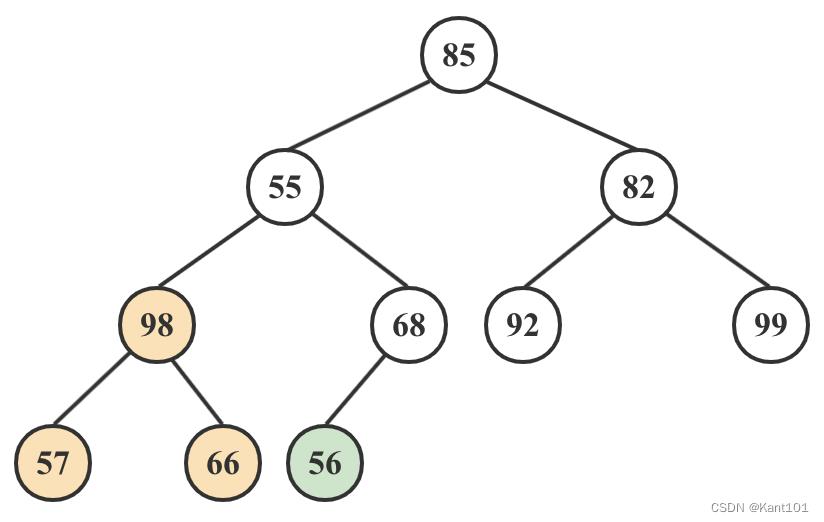
3）99和92与它们的父结点相比较，选择最大的做父结点，得到如下图

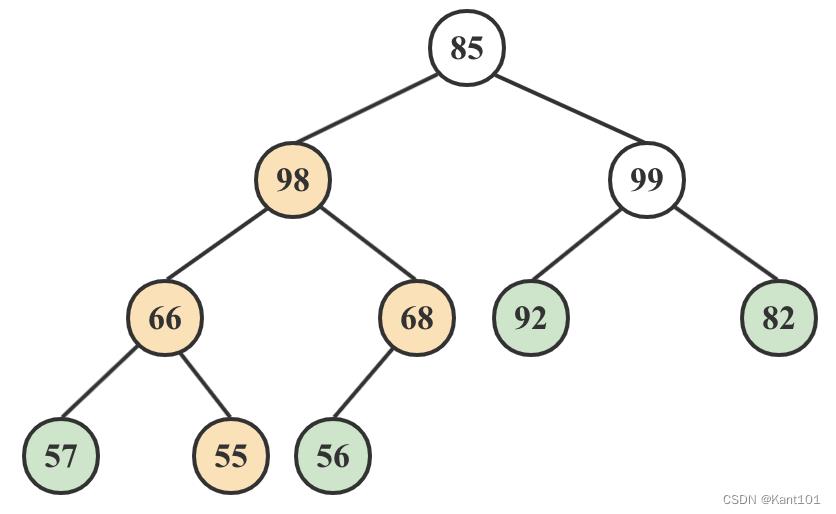
4）68和98与它们的父结点相比较，选择最大的98做父结点，即55和98交换。交换后还要对55进行递归，55比它的子结点小，继续调整，最终得到如下图：

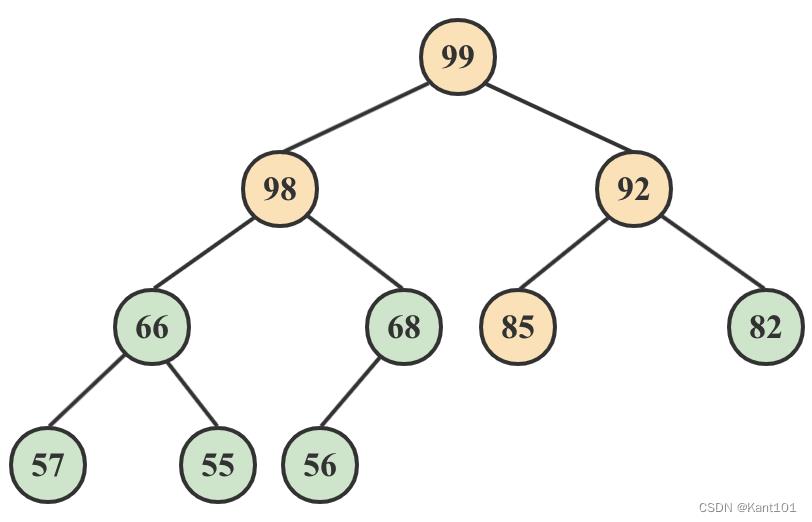
5）99和98与它们的父结点相比较，选择最大的99做父结点，即将85与99交换。交换后还需要对85递归，最终得到如下图：

最终，所有结点都进行了调整，得到了大顶堆如下：

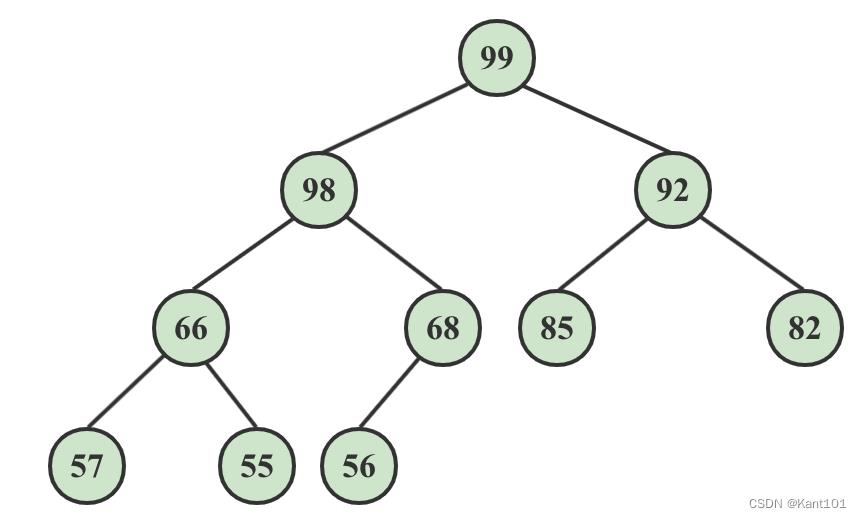
代码

const int maxn = 100;
//heap为堆，n为元素个数，heap数组有效数字下标要从1开始
int heap[maxn], n = 10;

/**
 * 对 heap 数组在 [low, high] 范围进行向下调整
 * 其中low为欲调整结点的下标，high一般为堆的最后一个元素的数组下标
 */
void downAdjust(int low, int high) 
    int i = low, j = i * 2; // i为欲调整结点，j为其左孩子
    while (j <= high)  //存在孩子结点
        // 如果右孩子存在，且右孩子的值大于左孩子
        if (j + 1 <= high && heap[j + 1] > heap[j]) 
            j = j + 1; // 让j存储右孩子下标
        
        // 如果孩子中最大的权值比欲调整结点i大
        if (heap[j] > heap[i]) 
            swap(heap[j], heap[i]); // 交换最大权值的孩子与欲调整结点i
            i = j; //保持i为欲调整结点，j为其左孩子
            j = i * 2;
         else 
            break; // 孩子的权值均比欲调整结点i小，调整结束
        
    

3. 堆排序

4. 测试

参考文献