数据结构：堆 的详解

Posted 正义的伙伴啊

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构：堆 的详解相关的知识，希望对你有一定的参考价值。

堆

文章目录

堆的概念及结构

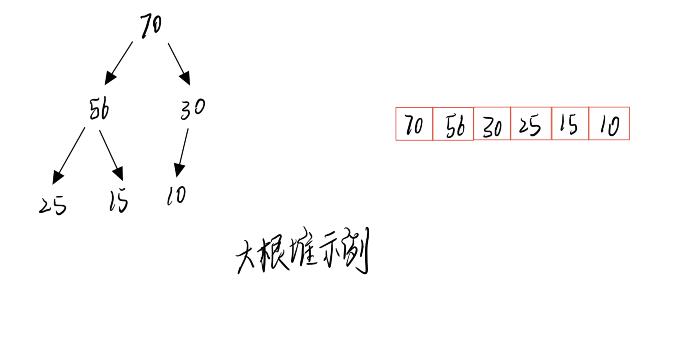
如果有一个关键码的集合k={k0,k1,k2…,kn-1}，把他们的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki<K(2i+1) 且 Ki<=K(2i+2) (或Ki>=K(2i+1) 且Ki>=K (2i+2) ) i=1,2,…，则称为小堆（大堆）。将根节点最大的堆叫做对大堆或大根堆，根节点最小的堆叫做小根堆

简单的来说堆实际上是一个数组，在物理结构（内存）中是连续存储的，但是逻辑上数据与数据之间的关系是一个二叉树

堆的性质

  • 堆中某个节点的值总是不大于或不小于其父节点的值
  • 堆总是一棵完全二叉树


堆的实现

向下调整算法（小根堆）

我们要想使一个数组调整成一个堆结构，就必须来了解向下调整算法
我们先从特殊的例子做起：
给定一个数组int arr[]={27,15,19,18,28,34,65,49,25,37};请把它调整成小根堆
这个数组十分的特殊如果我们画出他的逻辑图：

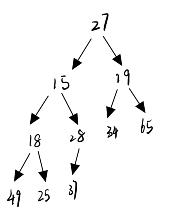
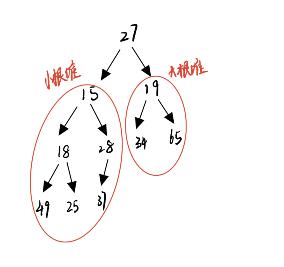
这个很显然就可以发现根的左子树和右子树都是小根堆，所以我们只要把根节点的值调整到合适的位置就可以了

这里就体现了向下调整的思想，首先看27的两个子节点，并找出两个子节点的最小值与27比较大小，27大于字节点的最小值15，所以不满足小根堆的条件顾要进行调整，即将最小的子节点和根节点调换位置
交换完成之后，就要以交换完成的位置为根节点，继续和他的子节点的最小值进行比较
在进行一次循环就可以完成小根堆的实现，将上面的思路总结下来就是
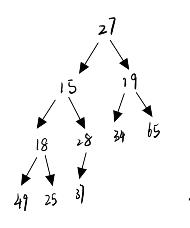
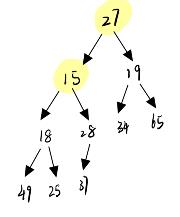
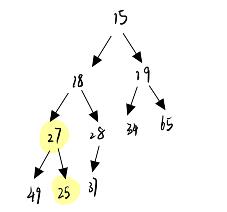
  • 首先求出子两个子节点最小值的下标
  • 然后用子节点最小值与根节点比较：
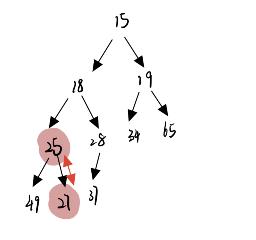
    1. 如果根节点比最小值大，那么就不满足小根堆的定义，所以将子节点与根节点交换，并继续向下重复上面的程序，直到子节点的下表超过数组的大小
    2. 如果根节点比最小值小，因为左右子树都是小根堆所以，根节点就是数组的最小值，便不用调整，直接结束就行了。

代码

void AdjustDown(int* a,int n,int parents)
{
	int child = 2 * parents + 1;
	while (child < n)
	{
		if (child+1<n && a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parents])
		{
			int temp = a[child];
			a[child] = a[parents];
			a[parents] = temp;
			parents = child;
			child = 2 * parents + 1;
		}
		else
		{
			break;
		}
	}
}

向上调整算法

向上排序算法和向下排序算法思路上都差不多

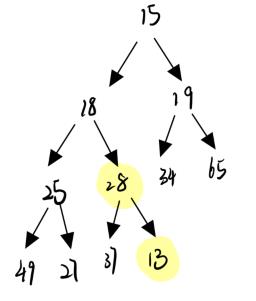
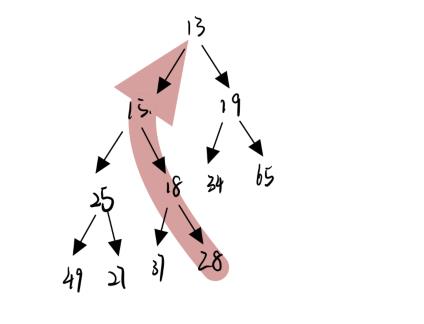
观察发现除了最底下的13，剩余的都是小根堆数组，所以只需要比较子节点和父节点的大小 如果发现
  1. 子节点比父节点小就交换，并把父节点当成子节点，利用关系求出他的父节点，向上比较，直到遇到根节点
  2. 子节点比父节点大，就已经使小根堆了，不用再继续比较了

代码

void AdjustUp(int* a, int n, int child)
{
	int parents = (child-1)/2;
	while (child > 0)
	{
		if (a[child] < a[parents])
		{
			int temp = a[child];
			a[child] = a[parents];
			a[parents] = temp;
			child = parents;
			parents = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

堆的创建

完成了 向上调整算法 和 向下调整算法就要实现堆了，在调整算法中只有一个数是不满足堆的条件，进行调整完成堆的实现。那如果给一个无序的数组该如何实现？

方法一（向下调整算法）

思路：由于向下调整算法需要 给定的父节点的 左子树 和 右子树必须是大根堆或小根堆
所以就必须从下往上调整，从最后一棵树开始，到根节点。这样每次的父节点下面的左子树和右子树都是小根堆。

void AdjustDown(int* a,int n,int parents)
{
	int child = 2 * parents + 1;
	while (child < n)
	{
		if (child+1<n && a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parents])
		{
			int temp = a[child];
			a[child] = a[parents];
			a[parents] = temp;
			parents = child;
			child = 2 * parents + 1;
		}
		else
		{
			break;
		}
	}

}
void HeapCreat(int a[], int n)
{
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		adjustdown(a, n, i);
	}
}

方法二（向上调整算法）

思路：由于向上调整算法需要 给的 子节点节点以上的树 必须是大根堆或小根堆
所以调整时就要从上向下调整，这样每次调整节点以上的树都是堆结构，直到最后一个数


void AdjustUp(int* a, int n, int child)
{
	int parents = (child-1)/2;
	while (child > 0)
	{
		if (a[child] < a[parents])
		{
			int temp = a[child];
			a[child] = a[parents];
			a[parents] = temp;
			child = parents;
			parents = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapCreat(int a[], int n)
{
	for (int i = 1; i < n; i++)
	{
		adjustup(a, n,i);
	}
}

建堆的时间复杂度

假设树的节点数有N个，则树的层数就有n=logN个
第一层，2^0个节点，需要向下移动n-1层
第二层，2^1个节点，需要向下移动n-2层
第三层，2^2个节点，需要向下移动n-3层
第四层，2^3个节点，需要向下移动n-4层
…

堆的模拟实现

堆是一种特殊的数据结构，因为其在物理结构上是一个数组，所以我们创建一个顺序表作为堆的结构：


typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int sz;
	int capacity;
}Heap;

其次我们还要完成一个堆的结构的创建的函数：

void HeapCreat(Heap** p)
{

	*p = (Heap*)malloc(sizeof(Heap));
	(*p)->a = (int*)malloc(4 * sizeof(int));
	(*p)->capacity = 4;
	(*p)->sz = 0;
}

下面进行堆的增加和删除元素

堆的增加元素——在堆尾插入并保持堆的结构不变

堆增加元素其实就是一个向上排序算法的实现，只不过子节点是数组最后一个增加进来的元素


void HeapPush(Heap* p, HPDataType x)
{
	HeapCheck(p);
	p->a[p->sz] = x;
	p->sz++;
	AdjustUp(p->a, p->sz, p->sz - 1);
}

堆减少元素——删除堆顶的数据，同时保持堆的结构不变

堆减少元素实际上要在向下排序的基础上小小的变形一下，如果直接删除堆顶的元素的话，根节点就变成第二个元素，堆的结构就会被破坏，就必须要重新建堆，所以这里采取的方法是：
将堆的最后一个元素和堆顶的元素交换，删除堆最后一个元素，并对整个堆进行一次向下调整

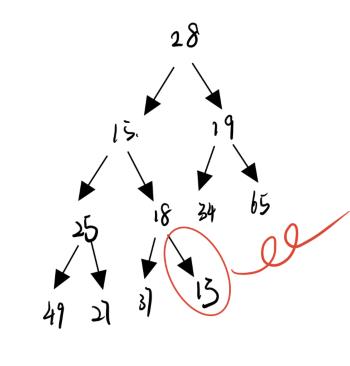
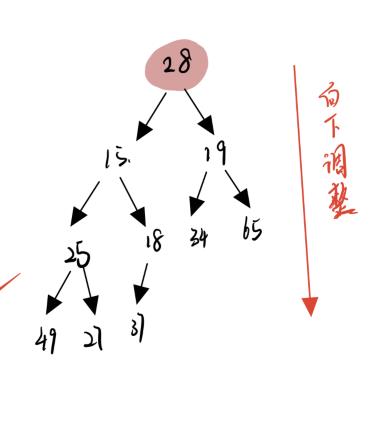
代码：

void AdjustDown(int* a,int n,int parents)
{
	int child = 2 * parents + 1;
	while (child < n)
	{
		if (child+1<n && a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parents])
		{
			int temp = a[child];
			a[child] = a[parents];
			a[parents] = temp;
			parents = child;
			child = 2 * parents + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(Heap* p)
{
	swap(&p->a[p->sz - 1], &p->a[0]);
	AdjustDown(p->a, p->sz - 1, 0);
}

堆的应用

堆排序

利用堆实现对一个数组的排序，我们要了解的是堆这个结构如果只是建了一个堆是无法得到一个升序或降序的数组，因为同一层的元素的大小是无法确定的。但是堆唯一可以确定的是堆顶的元素是该堆所有元素的最大值或最小值，所以这里排序的思想就是在不破坏堆的结构的情况下，将堆顶的数一个一个拿走，这样就得到了一个有序的数组。
要想不破坏堆的结构在建堆的时候就要注意：

  • 升序建大堆
  • 降序建小堆

以升序为例：先建了一个n个数大堆，将堆顶的值（最大值同时还是数组的首元素）与 数组的最后一个值交换，这样我们就把最大值放到了数组结尾，然后对除了最大值以外的n-1个数据向下排序，这时的堆顶就是第二大的值，重复上述动作。


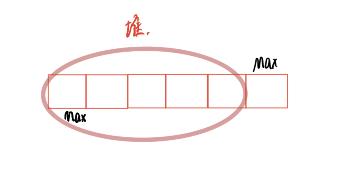
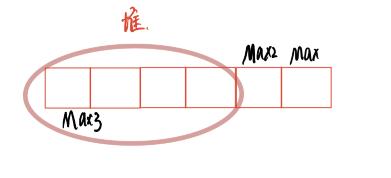
代码：

void swap(int* a, int* b)
{
	int temp = *a;
	*a = *b;
	*b = temp;
}
void adjustdown(int a[], int n, int parents)
{
	int child = parents * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child] > a[child + 1])
		{
			child++;
		}
		if (a[parents] > a[child])
		{
			swap(&a[parents], &a[child]);
			parents = child;
			child = parents * 2 + 1;
		}
		else
		{
			break;
		}
	}

}
void sort(int a[], int n)
{
	for (int i = 1; i < n; i++)//建堆
	{
		adjustup(a, n,i);
	}

	for (int j = 1; j < n; j++)
	{
		swap(&a[0], &a[n - j]);
		adjustdown(a, n - j, 0);//每次将堆顶的元素（数组末端的交换值）向下排序
	}
}
}

TopK问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小元素，一般情况下数据量都比较大
步骤：

  1. 用数据集合中前K个元素来建堆

          - 前K个最大的元素，建小堆
      - 前K个最小的元素，建大堆

  2. 用剩余的N-K个元素与堆顶元素来比较，不满足则替换堆顶元素

          - 将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的就是所求的前K个最小或最大的元素


void PrintTopK(int* a, int n, int k)
{
	for (int i = (k-2)/2; i >=0; i--)
	{
		AdjustDown(a, k, i);
	}
	for (int i = k; i < n; i++)
	{
		if (a[i] > a[0])
		{
			int temp = a[i];
			a[i] = a[0];
			a[0] = temp;
			for (int i = (k - 2) / 2; i >= 0; i--)
			{
				AdjustDown(a, k, i);
			}
		}
	}
	for (int i = 0; i < k; i++)
	{
		printf(" %d ", a[i]);
	}
}
int main()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand(time(0));
	for (size_t i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
	a[5] = 100000 + 1;
	a[1231] = 100000 + 2;
	a[531] = 100000 + 3;
	a[5121] = 100000 + 4;
	a[115] = 100000 + 5;
	a[2335] = 100000 + 6;
	a[9999] = 100000 + 7;
	a[76] = 100000 + 8;
	a[423] = 100000 + 9;
	a[3144] = 100000 + 10;
	PrintTopK(a, 10000, 10);
}

在main函数里检验：人为的创造一个最大K个值已知的顺序表，打印结果如下：

以上是关于数据结构：堆 的详解的主要内容，如果未能解决你的问题，请参考以下文章

二叉树，堆详解

排序：Java实现大顶堆和二叉树的广度优先遍历原理及代码注释详解

(转) Java中的负数及基本类型的转型详解

堆结构及堆排序详解

详解Android WebView加载html片段

数据结构堆及堆排序详解