PCB 加投率计算实现基本原理--K最近邻算法(KNN)
Posted pcbren
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了PCB 加投率计算实现基本原理--K最近邻算法(KNN)相关的知识,希望对你有一定的参考价值。
PCB行业中,客户订购5000pcs,在投料时不会直接投5000pcs,因为实际在生产过程不可避免的造成PCB报废,
所以在生产前需计划多投一定比例的板板,
例:订单 量是5000pcs,加投3%,那就是总共投料要投料5000*1.03=5150pcs。
而这个多投的订单标准,每家工厂都可能不一样的,因为加投比例,需要结合订单数量,层数,铜厚,线宽,线距,
表面工艺,HDI阶数,孔径比,特殊工艺,验收标准等等 ,所以工艺难度越大,加投量也是越多。
在这里以K最近邻算法(KNN)进行加投率的模似
K最近邻 (k-Nearest Neighbors,KNN) 算法是一种分类算法,也是最简单易懂的机器学习算法,没有之一。1968年由 Cover 和 Hart 提出,应用场景有字符识别、文本分类、图像识别等领域。该算法的思想是:一个样本与数据集中的k个样本最相似,如果这k个样本中的大多数属于某一个类别,则该样本也属于这个类别。当然实际情况不可能这么简单,这里只是为了说明该算法的用法。
这里举例是对单个蚀刻工序加投率模拟,而对整个订单 的加投模拟要复杂得多
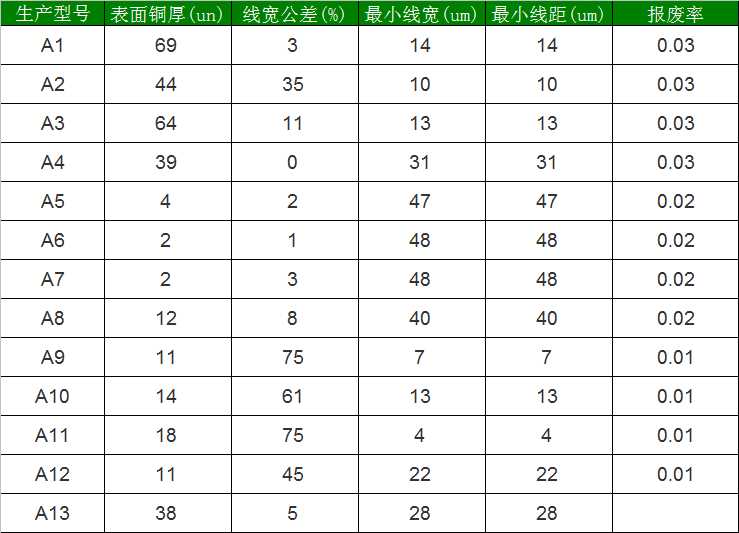
先准备下面数据集中序号A1-A12为生产型号,为已知的蚀刻工序关键对报废影响的关键参数,分为表面铜厚、线宽公差、最小线宽、最小线距4个类,
(此数据是参数对此工序的影响权重值,并非真实的值, 为了简化:报废多少量就是因该要加投多少量)
表格中最下的A13的生产型号,对应的关键参数(表面铜厚、线宽公差、最小线宽、最小线距)已有了,
但如何预测A13这款板的加投率呢。
原理:通过A13这款板的产品信息与历史生产过的产品信息,用欧式距离是一个非常简单又最常用的距离计算方法。
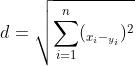 值越小,就是匹配度就越高, 而为了保证预测的结果准确,通过会将前几个匹配度最高的值中取出现频率最高的.
值越小,就是匹配度就越高, 而为了保证预测的结果准确,通过会将前几个匹配度最高的值中取出现频率最高的.
一.建立数据结构类
public class ModTechData { /// <summary> /// 生产型号 /// </summary> public string pdctno { get; set; } /// <summary> /// 表面铜厚 /// </summary> public int CuThickness { get; set; } /// <summary> /// 线宽公差 /// </summary> public int Tolerance { get; set; } /// <summary> /// 最小线宽 /// </summary> public int Width { get; set; } /// <summary> /// 最小线距 /// </summary> public int Space { get; set; } /// <summary> /// 报废率 /// </summary> public double Scrap { get; set; } /// <summary> /// KNN距离 /// </summary> public double KNN { get; set; } }
二.构建数据;
List<ModTechData> TechDataList = new List<ModTechData>() { new ModTechData(){ pdctno = "A1", CuThickness = 69, Tolerance = 3, Width = 14, Space = 14, Scrap = 0.03} ,new ModTechData(){ pdctno = "A2", CuThickness = 44, Tolerance = 35, Width = 10, Space = 10, Scrap = 0.03} ,new ModTechData(){ pdctno = "A3", CuThickness = 64, Tolerance = 11, Width = 13, Space = 13, Scrap = 0.03} ,new ModTechData(){ pdctno = "A4", CuThickness = 39, Tolerance = 0, Width = 31, Space = 31, Scrap = 0.03} ,new ModTechData(){ pdctno = "A5", CuThickness = 4, Tolerance = 2, Width = 47, Space = 47, Scrap = 0.02} ,new ModTechData(){ pdctno = "A6", CuThickness = 2, Tolerance = 1, Width = 48, Space = 48, Scrap = 0.02} ,new ModTechData(){ pdctno = "A7", CuThickness = 2, Tolerance = 3, Width = 48, Space = 48, Scrap = 0.02} ,new ModTechData(){ pdctno = "A8", CuThickness = 12, Tolerance = 8, Width = 40, Space = 40, Scrap = 0.02} ,new ModTechData(){ pdctno = "A9", CuThickness = 11, Tolerance = 75, Width = 7, Space = 7, Scrap = 0.01} ,new ModTechData(){ pdctno = "A10", CuThickness = 14, Tolerance = 61, Width = 13, Space = 13, Scrap = 0.01} ,new ModTechData(){ pdctno = "A11", CuThickness = 18, Tolerance = 75, Width = 4, Space = 4, Scrap = 0.01} ,new ModTechData(){ pdctno = "A12", CuThickness = 11, Tolerance = 45, Width = 22, Space = 22, Scrap = 0.01} };
三.计算A13数据与数据集中所有数据的距离。
ModTechData TechData = new ModTechData() { pdctno = "A13", CuThickness = 38, Tolerance = 5, Width = 28, Space = 28 }; foreach (var item in TechDataList) { var CuThicknessDiff = Math.Pow(TechData.CuThickness - item.CuThickness, 2); var ToleranceDiff = Math.Pow(TechData.Tolerance - item.Tolerance, 2); var WidthDiff = Math.Pow(TechData.Width - item.Width, 2); var SpaceeDiff = Math.Pow(TechData.Space - item.Space, 2); item.KNN = Math.Sqrt(CuThicknessDiff + ToleranceDiff + WidthDiff + SpaceeDiff); }
四.按照距离大小进行递增排序,选取距离最小的k个样本
由于样本数量只有12个,取前5个匹配度最高的,如果实际应有样本量越多可以调整K值
var TechDataSortList = TechDataList.OrderBy(tt => tt.KNN).Take(5).ToList();

五.确定前k个样本所在类别出现的频率,取出现频率最高的类别
通过此算法,得到了A13这款板加投率匹配后频率最高加投率是0.03(3%)
var TechDataGroupList =TechDataSortList.GroupBy(tt => tt.Scrap).Select(tt => new { key = tt.Key, count = tt.Count() }).ToList();

六.真实预测加率的挑战
我们通常正常理解:比如一个产品有20个工序,将每一道工序加投率值计算出来,最终相加并得出此产品最终的加投率不就OK了吗。
但实际并不是这么简单,
1.影响工序的特征值不仅限于单工序计算加投,需综合计考虑,局部加投与综合加投,结合分析得到最终加投率
2.不仅限于当前工序的参数影响值计算加投,需考虑前工序设备参数会对后工序的影响,对历史生产的订单机器设备参数采集,覆盖越全预测才准
3.此算法是基于历史数据预测结果,样本量越大,样板特征覆盖率越全,准确率高。为了保证样本数据量在递增,每次加投或补投都需更新样板库。
4.若想预测结果准确一定要确保样本参数与结果是OK的,不然会影响加投预测的偏差。
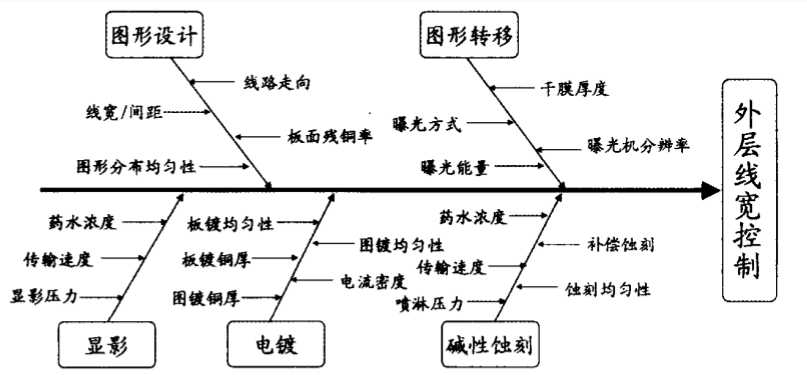
下图是外层线宽控制鱼骨图,影响线宽参数如此广泛,而想要精准预测加投率也是同样需将影响加投的因素分析出来的。
七.KNN有几个特点:
(1)KNN属于惰性学习(lazy-learning)
这是与急切学习(eager learning)相对应的,因为KNN没有显式的学习过程!也就是说没有训练阶段,从上面的例子就可以看出,数据集事先已有了分类和特征值,待收到新样本后直接进行处理。
(2)KNN的计算复杂度较高
我们从上面的例子可以看到,新样本需要与数据集中每个数据进行距离计算,计算复杂度和数据集中的数据数目n成正比,也就是说,KNN的时间复杂度为O(n),因此KNN一般适用于样本数较少的数据集。
(3)k取不同值时,分类结果可能会有显著不同。
一般k的取值不超过20,上限是n的开方
以上是关于PCB 加投率计算实现基本原理--K最近邻算法(KNN)的主要内容,如果未能解决你的问题,请参考以下文章