K近邻算法小结
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了K近邻算法小结相关的知识,希望对你有一定的参考价值。
参考技术AK近邻一种非参数学习的算法,可以用在分类问题上,也可以用在回归问题上。
算法简单 ,模型容易理解,没有学习训练过程,通常情况下不需要做很大调整就有着不错的表现;因此 通常用作一个问题的baseline(最差、最基本的解决方案)
史诗级干货长文K-近邻算法
K-近邻算法
前言
机器学习入门算法:KNN算法
学习目标:
- 掌握K-近邻算法实现过程
- 知道K-近邻算法的距离公式
- 知道K-近邻算法的超参数K值以及取值问题
- 知道kd树实现搜索的过程
- 应用KNeighborsClassifier实现分类
- 知道K-近邻算法的优缺点
- 知道交叉验证实现过程
- 知道超参数搜索过程
- 应用GridSearchCV实现算法参数的调优
1. K-近邻算法简介
1.1 什么是K-近邻算法
- 根据你的“邻居”来推断出你的类别
1.2 K-近邻算法(KNN)概念
K Nearest Neighbor算法又叫KNN算法,这个算法是机器学习里面一个比较经典的算法, 总体来说KNN算法是相对比较容易理解的算法。
- 定义
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
来源:KNN算法最早是由Cover和Hart提出的一种分类算法
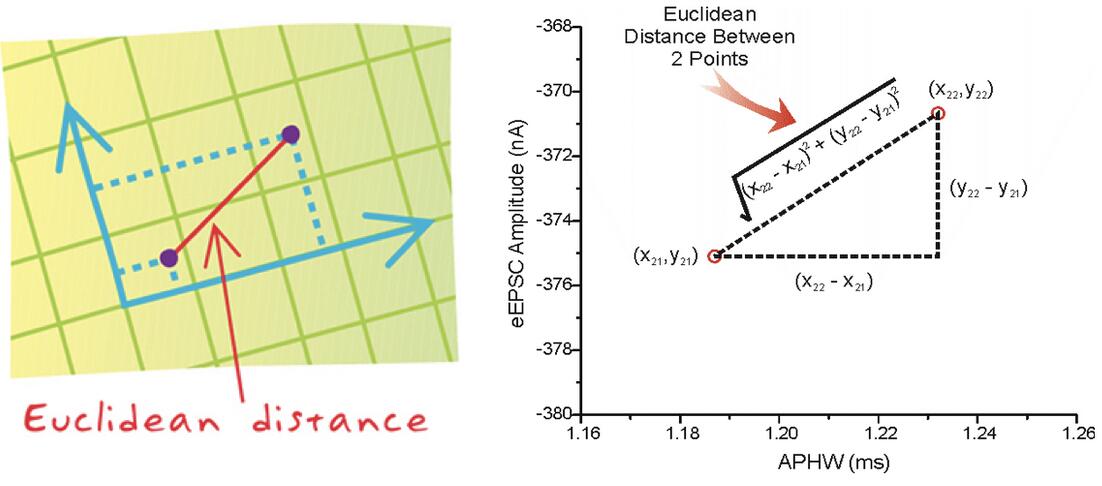
- 距离公式
两个样本的距离可以通过如下公式计算,又叫欧式距离 ,关于距离公式会在后面进行讨论。

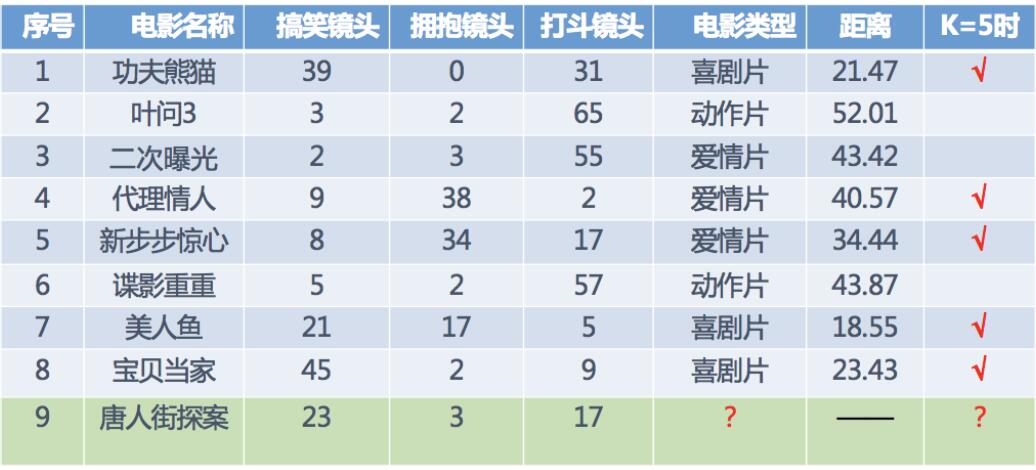
1.3 电影类型分析
假设我们现在有几部电影
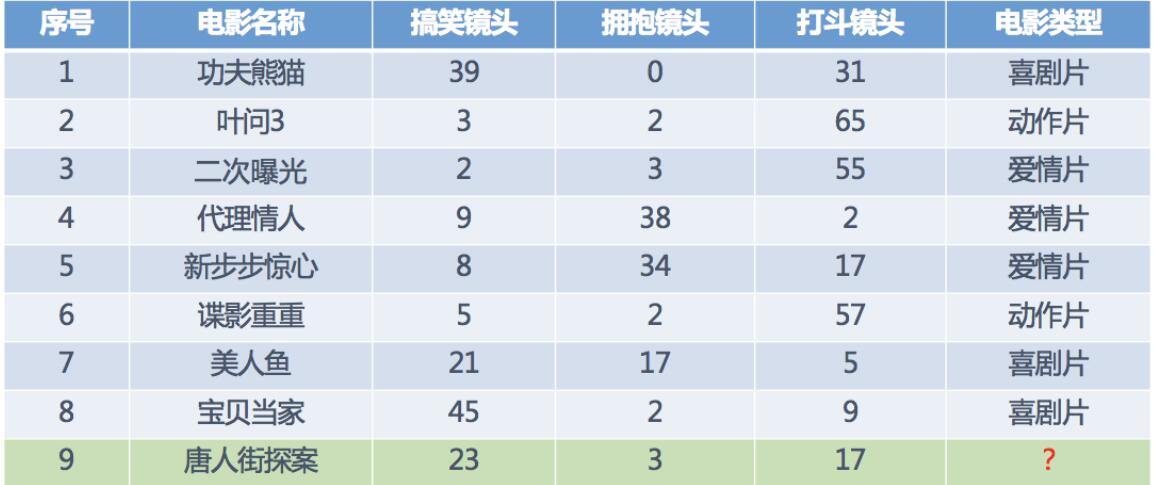
其中 ?号电影不知道类别,如何去预测?我们可以利用K近邻算法的思想。
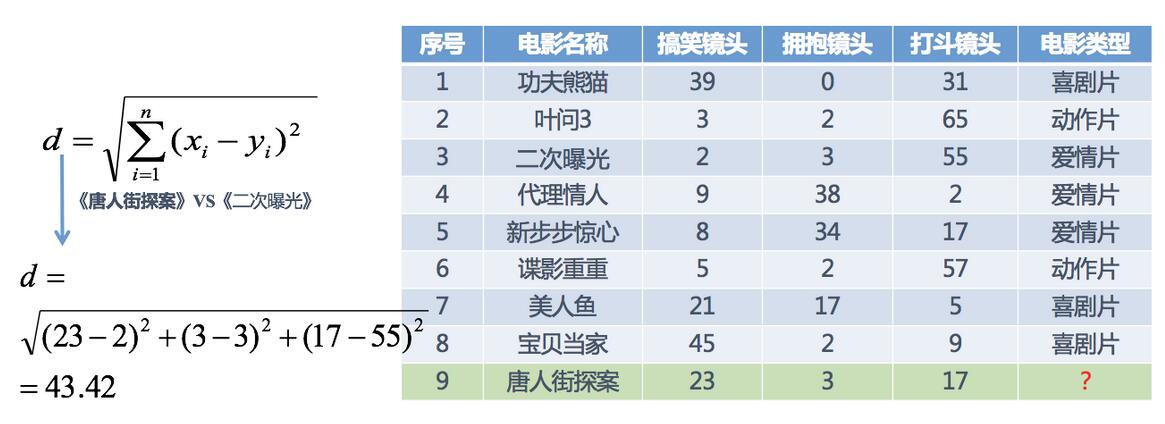
分别计算每个电影和被预测电影的距离,然后求解
1.4 KNN算法流程总结
1)计算已知类别数据集中的点与当前点之间的距离
2)按距离递增次序排序
3)选取与当前点距离最小的k个点
4)统计前k个点所在的类别出现的频率
5)返回前k个点出现频率最高的类别作为当前点的预测分类
K-近邻算法
定义:就是通过你的"邻居"来判断你属于哪个类别
如何计算你到你的"邻居"的距离:一般时候,都是使用欧氏距离
2. KNN算法API初步使用
机器学习流程复习:
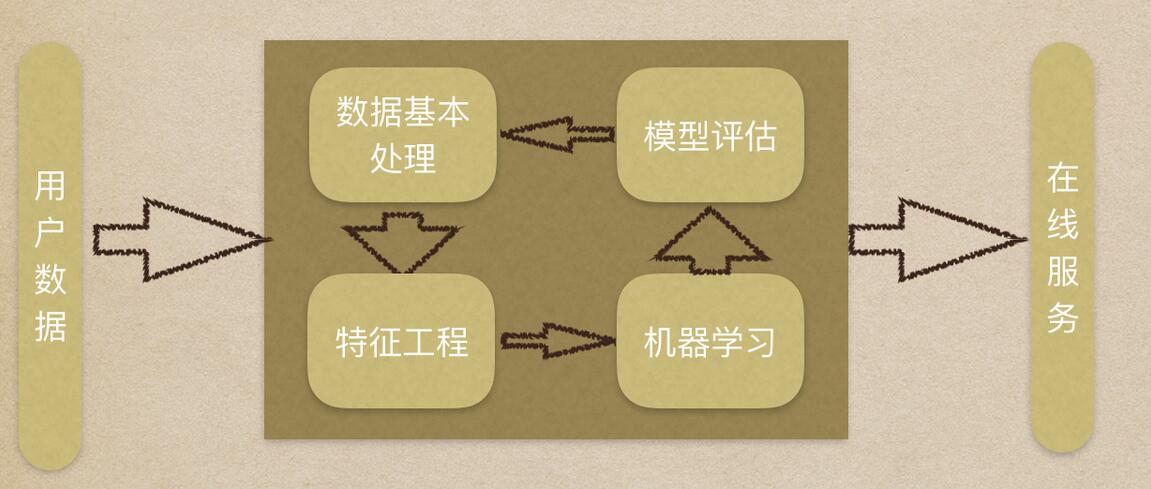
- 1.获取数据集
- 2.数据基本处理
- 3.特征工程
- 4.机器学习
- 5.模型评估
2.1 Scikit-learn工具介绍

- Python语言的机器学习工具
- Scikit-learn包括许多知名的机器学习算法的实现
- Scikit-learn文档完善,容易上手,丰富的API
- 目前稳定版本0.19.1
2.1.1 安装Scikit-learn
pip3 install scikit-learn==0.19.1
安装好之后可以通过以下命令查看是否安装成功
import sklearn
- 注:安装
scikit-learn需要Numpy, Scipy等库
安装scikit-learn,速度较慢,建议参考:【我的pip终于神速了】解决pip安装速度慢的问题 快速安装。
2.1.2 Scikit-learn包含的内容

- 分类、聚类、回归
- 特征工程
- 模型选择、调优
2.2 K-近邻算法API
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
*n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数
2.3 案例
2.3.1 步骤分析
- 1.获取数据集
- 2.数据基本处理(该案例中省略)
- 3.特征工程(该案例中省略)
- 4.机器学习
- 5.模型评估(该案例中省略)
2.3.2 代码过程
- 导入模块
from sklearn.neighbors import KNeighborsClassifier
- 构造数据集
x = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
- 机器学习 – 模型训练
# 实例化API
estimator = KNeighborsClassifier(n_neighbors=2)
# 使用fit方法进行训练
estimator.fit(x, y)
estimator.predict([[1]])
2.4 小结
- sklearn的优势:
- 文档多,且规范
- 包含的算法多
- 实现起来容易
- knn中的api
- sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
3. 距离度量
3.1 欧式距离(Euclidean Distance)
3.2 曼哈顿距离(Manhattan Distance)
3.3 切比雪夫距离 (Chebyshev Distance)
3.4 闵可夫斯基距离(Minkowski Distance)
3.5 标准化欧氏距离 (Standardized EuclideanDistance)
3.6 余弦距离(Cosine Distance)
3.7 汉明距离(Hamming Distance)
3.8 杰卡德距离(Jaccard Distance)
3.9 马氏距离(Mahalanobis Distance)
请参考: 【机器学习】距离度量中常见的距离计算公式
4. k值的选择
4.1 k值选择说明
举例说明:
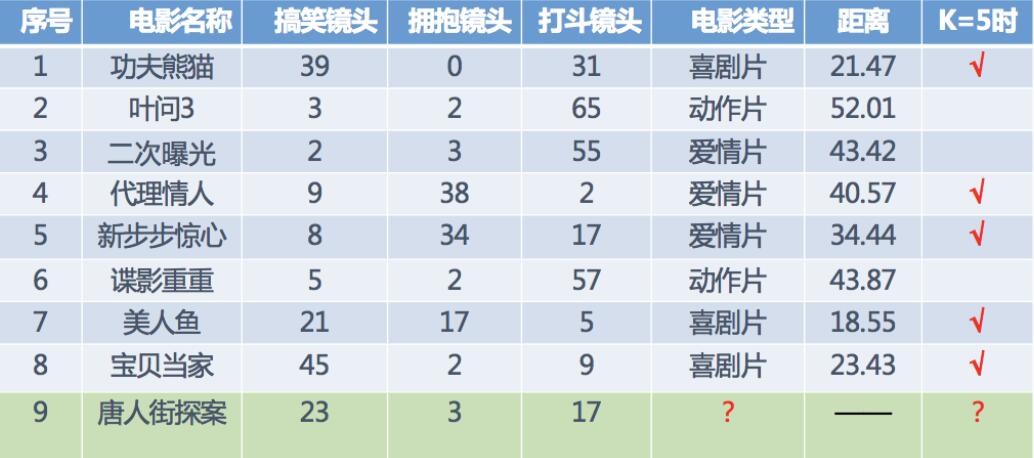
- k值过小:
- 容易受到异常点的影响
- k值过大:
- 受到样本均衡的问题
K值选择问题,李航博士的一书「统计学习方法」上所说:
-
选择较小的K值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
-
选择较大的K值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。
-
K=N(N为训练样本个数),则完全不足取,因为此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的类,模型过于简单,忽略了训练实例中大量有用信息。
- 近似误差:
- 对现有训练集的训练误差,关注训练集,
- 如果近似误差过小可能会出现过拟合的现象,对现有的训练集能有很好的预测,但是对未知的测试样本将会出现较大偏差的预测。
- 模型本身不是最接近最佳模型。
- 估计误差:
- 可以理解为对测试集的测试误差,关注测试集,
- 估计误差小说明对未知数据的预测能力好,
- 模型本身最接近最佳模型。
4.2 小结
- KNN中K值大小选择对模型的影响
- K值过小:
- 容易受到异常点的影响
- 容易过拟合
- K值过大:
- 受到样本均衡的问题
- 容易欠拟合
- K值过小:
5. kd树
问题导入:
实现k近邻算法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索。
这在特征空间的维数大及训练数据容量大时尤其必要。
k近邻法最简单的实现是线性扫描(穷举搜索),即要计算输入实例与每一个训练实例的距离。计算并存储好以后,再查找k近邻。当训练集很大时,计算非常耗时。
为了提高KNN搜索的效率,可以考虑使用特殊的结构存储训练数据,以减小计算距离的次数。
5.1 kd树简介
5.1.1 什么是kd树
根据KNN每次需要预测一个点时,我们都需要计算训练数据集里每个点到这个点的距离,然后选出距离最近的k个点进行投票。当数据集很大时,这个计算成本非常高。
kd树:为了避免每次都重新计算一遍距离,算法会把距离信息保存在一棵树里,这样在计算之前从树里查询距离信息,尽量避免重新计算。其基本原理是,如果A和B距离很远,B和C距离很近,那么A和C的距离也很远。有了这个信息,就可以在合适的时候跳过距离远的点。
这样优化后的算法复杂度可降低到 O(DNlog(N))。感兴趣的读者可参阅论文:Bentley,J.L.,Communications of the ACM(1975)。
1989年,另外一种称为Ball Tree的算法,在kd Tree的基础上对性能进一步进行了优化。感兴趣的读者可以搜索Five balltree construction algorithms来了解详细的算法信息。
5.1.2 原理
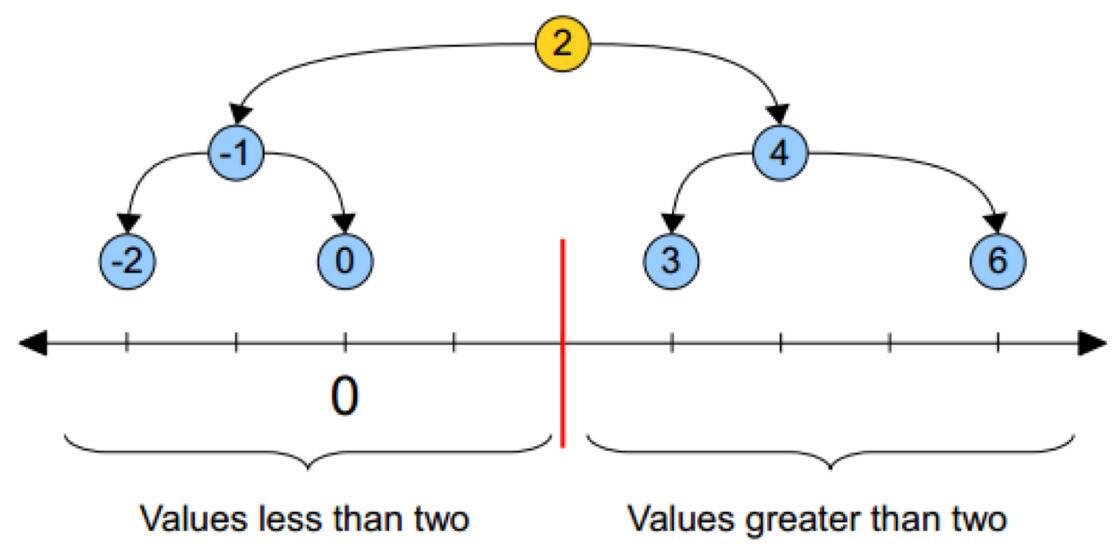
黄色的点作为根节点,上面的点归左子树,下面的点归右子树,接下来再不断地划分,分割的那条线叫做分割超平面(splitting hyperplane),在一维中是一个点,二维中是线,三维的是面。
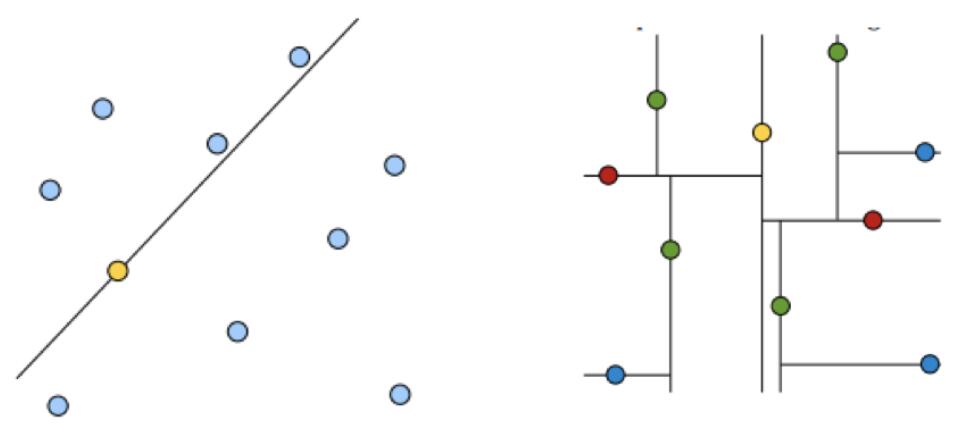
黄色节点就是Root节点,下一层是红色,再下一层是绿色,再下一层是蓝色。
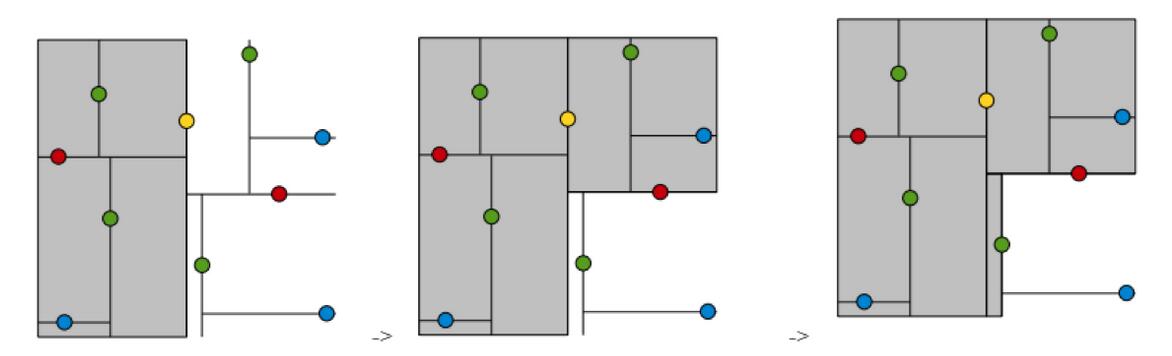
1.树的建立;
2.最近邻域搜索(Nearest-Neighbor Lookup)
kd树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是一种二叉树,表示对k维空间的一个划分,构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分,构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
类比“二分查找”:给出一组数据:[9 1 4 7 2 5 0 3 8],要查找8。如果挨个查找(线性扫描),那么将会把数据集都遍历一遍。而如果排一下序那数据集就变成了:[0 1 2 3 4 5 6 7 8 9],按前一种方式我们进行了很多没有必要的查找,现在如果我们以5为分界点,那么数据集就被划分为了左右两个“簇” [0 1 2 3 4]和[6 7 8 9]。
因此,根本就没有必要进入第一个簇,可以直接进入第二个簇进行查找。把二分查找中的数据点换成k维数据点,这样的划分就变成了用超平面对k维空间的划分。空间划分就是对数据点进行分类,“挨得近”的数据点就在一个空间里面。
5.2 构造方法
(1)构造根结点,使根结点对应于K维空间中包含所有实例点的超矩形区域;
(2)通过递归的方法,不断地对k维空间进行切分,生成子结点。在超矩形区域上选择一个坐标轴和在此坐标轴上的一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴,将当前超矩形区域切分为左右两个子区域(子结点);这时,实例被分到两个子区域。
(3)上述过程直到子区域内没有实例时终止(终止时的结点为叶结点)。在此过程中,将实例保存在相应的结点上。
(4)通常,循环的选择坐标轴对空间切分,选择训练实例点在坐标轴上的中位数为切分点,这样得到的kd树是平衡的(平衡二叉树:它是一棵空树,或其左子树和右子树的深度之差的绝对值不超过1,且它的左子树和右子树都是平衡二叉树)。
KD树中每个节点是一个向量,和二叉树按照数的大小划分不同的是,KD树每层需要选定向量中的某一维,然后根据这一维按左小右大的方式划分数据。在构建KD树时,关键需要解决2个问题:
(1)选择向量的哪一维进行划分;
(2)如何划分数据;
第一个问题简单的解决方法可以是随机选择某一维或按顺序选择,但是更好的方法应该是在数据比较分散的那一维进行划分(分散的程度可以根据方差来衡量)。
第二个问题中,好的划分方法可以使构建的树比较平衡,可以每次选择中位数来进行划分。
5.3 案例分析
5.3.1 树的建立
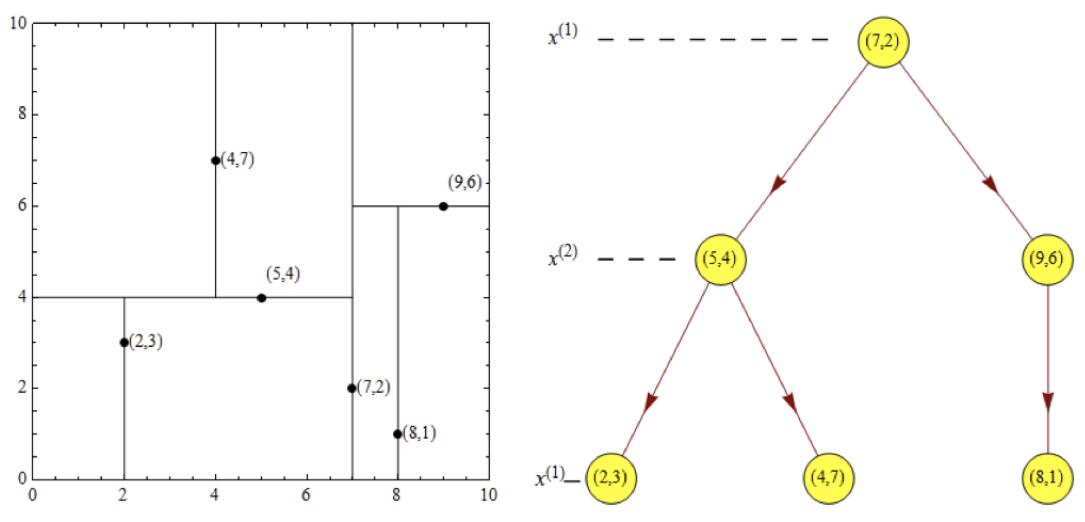
给定一个二维空间数据集:T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},构造一个平衡kd树。
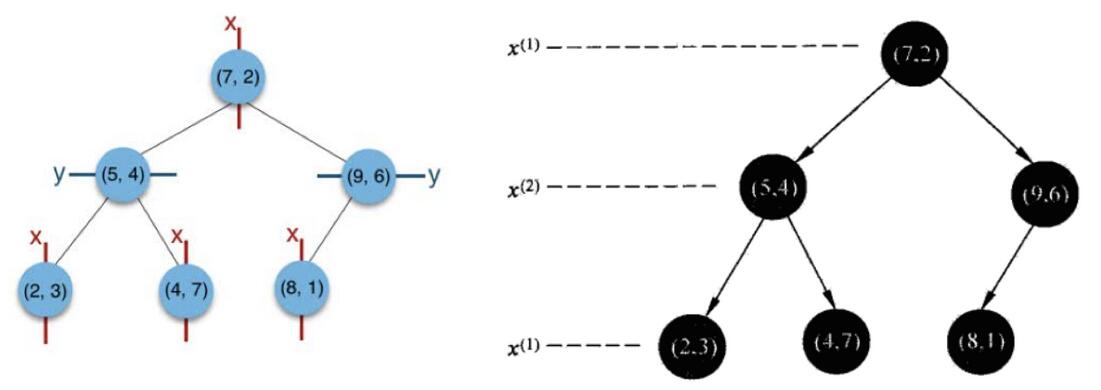
(1)思路引导:
根结点对应包含数据集T的矩形,选择x(1)轴,6个数据点的x(1)坐标中位数是6,这里选最接近的(7,2)点,以平面x(1)=7将空间分为左、右两个子矩形(子结点);接着左矩形以x(2)=4分为两个子矩形(左矩形中{(2,3),(5,4),(4,7)}点的x(2)坐标中位数正好为4),右矩形以x(2)=6分为两个子矩形,如此递归,最后得到如下图所示的特征空间划分和kd树。
5.3.2 最近领域的搜索
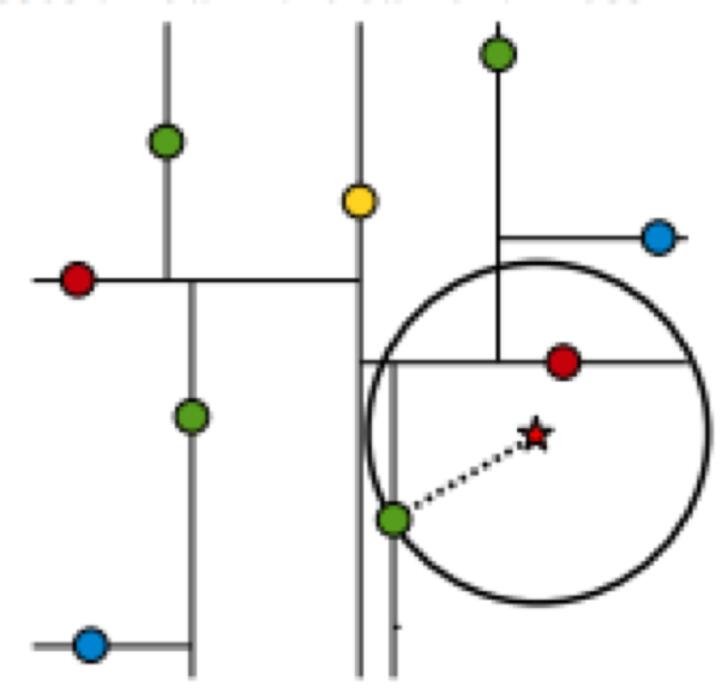
假设标记为星星的点是 test point, 绿色的点是找到的近似点,在回溯过程中,需要用到一个队列,存储需要回溯的点,在判断其他子节点空间中是否有可能有距离查询点更近的数据点时,做法是以查询点为圆心,以当前的最近距离为半径画圆,这个圆称为候选超球(candidate hypersphere),如果圆与回溯点的轴相交,则需要将轴另一边的节点都放到回溯队列里面来。
样本集 {(2,3),(5,4), (9,6), (4,7), (8,1), (7,2)}
- 查找点(2.1,3.1)
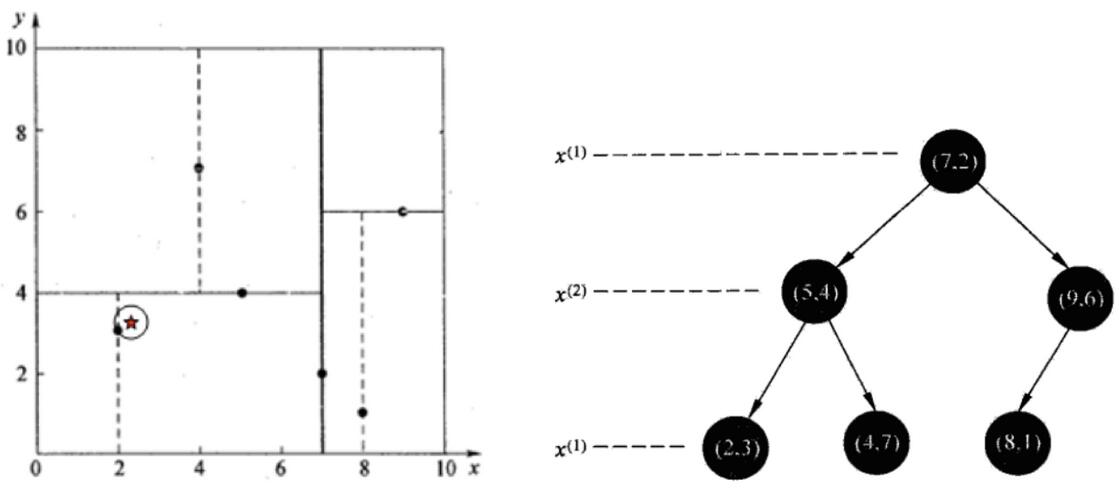
在(7,2)点测试到达(5,4),在(5,4)点测试到达(2,3),然后search_path中的结点为<(7,2),(5,4), (2,3)>,从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141;
然后回溯至(5,4),以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆,并不和超平面y=4相交,如上图,所以不必跳到结点(5,4)的右子空间去搜索,因为右子空间中不可能有更近样本点了。
于是再回溯至(7,2),同理,以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆并不和超平面x=7相交,所以也不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2.1,3.1)的最近邻点,最近距离为0.141。
- 查找点(2,4.5)
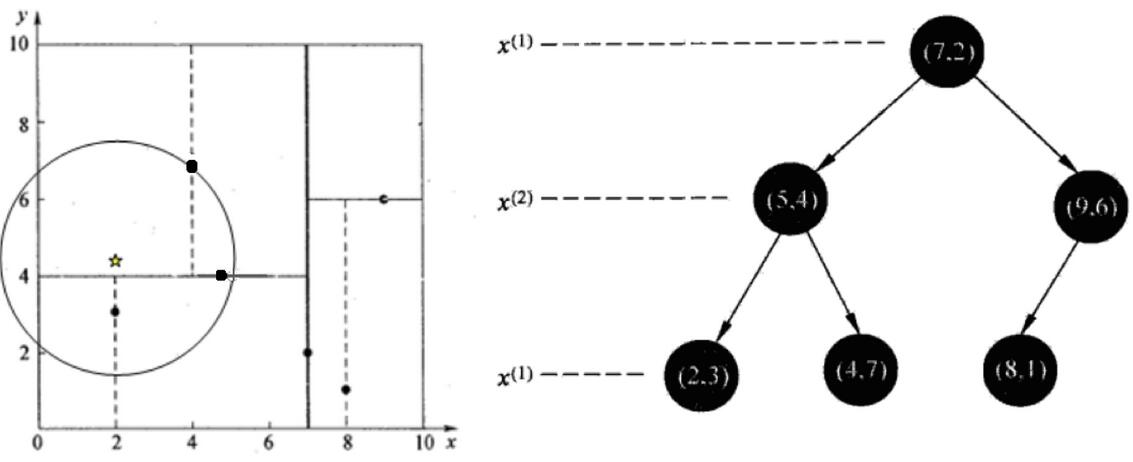
在(7,2)处测试到达(5,4),在(5,4)处测试到达(4,7)【优先选择在本域搜索】,然后search_path中的结点为<(7,2),(5,4), (4,7)>,从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202;
然后回溯至(5,4),以(2,4.5)为圆心,以dist=3.202为半径画一个圆与超平面y=4相交,所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中,现在search_path中的结点为<(7,2),(2, 3)>;另外,(5,4)与(2,4.5)的距离为3.04 < dist = 3.202,所以将(5,4)赋给nearest,并且dist=3.04。
回溯至(2,3),(2,3)是叶子节点,直接平判断(2,3)是否离(2,4.5)更近,计算得到距离为1.5,所以nearest更新为(2,3),dist更新为(1.5)
回溯至(7,2),同理,以(2,4.5)为圆心,以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2,4.5)的最近邻点,最近距离为1.5。
5.4 总结
- kd树的构建过程
- 1.构造根节点
- 2.通过递归的方法,不断地对k维空间进行切分,生成子节点
- 3.重复第二步骤,直到子区域中没有示例时终止
- 需要关注细节:a.选择向量的哪一维进行划分;b.如何划分数据
- kd树的搜索过程
- 1.二叉树搜索比较待查询节点和分裂节点的分裂维的值,(小于等于就进入左子树分支,大于就进入右子树分支直到叶子结点)
- 2.顺着“搜索路径”找到最近邻的近似点
- 3.回溯搜索路径,并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点,如果有可能,则需要跳到其他子结点空间中去搜索
- 4.重复这个过程直到搜索路径为空
6. 鸢尾花种类预测–数据集介绍
鸢尾花种类预测–数据集介绍
本实验介绍了使用Python进行机器学习的一些基本概念。 在本案例中,将使用 K-Nearest Neighbor(KNN) 算法对鸢尾花的种类进行分类,并测量花的特征。
本案例目的:
- 遵循并理解完整的机器学习过程
- 对机器学习原理和相关术语有基本的了解。
- 了解评估机器学习模型的基本过程。
请参考:【K-近邻算法】鸢尾花种类预测
7. 特征工程–特征预处理
学习目标
- 了解什么是特征预处理
- 知道归一化和标准化的原理及区别
8. 鸢尾花种类预测–流程实现
学习目标
知道KNeighborsClassifier的用法
9. K-近邻算法总结
优点:
- 简单有效
- 重新训练的代价低
- 适合类域交叉样本
- KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
- 适合大样本自动分类
- 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
缺点:
- 惰性学习
- KNN算法是懒散学习方法(lazy learning,基本上不学习),一些积极学习的算法要快很多
- 类别评分不是规格化
- 不像一些通过概率评分的分类
- 输出可解释性不强
例如决策树的输出可解释性就较强 - 对不均衡的样本不擅长
- 当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
- 计算量较大
- 目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
10. 交叉验证,网格搜索
学习目标
- 知道交叉验证、网格搜索的概念
- 会使用交叉验证、网格搜索优化训练模型
加油!
感谢!
努力!
以上是关于K近邻算法小结的主要内容,如果未能解决你的问题,请参考以下文章