K近邻法(KNN)原理小结

Posted 2021-01-27 hum0ro

　　

一、绪论

　　　K近邻法(k-nearest neighbors,KNN)是一种很基本的机器学习方法了，在我们平常的生活中也会不自主的应用。比如，我们判断一个人的人品，只需要观察他来往最密切的几个人的人品好坏就可以得出了。这里就运用了KNN的思想。KNN方法既可以做分类，也可以做回归，这点和决策树算法相同。

　　　KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同。KNN做分类预测时，一般是选择多数表决法(少数服从多数)，即训练集里和预测的样本特征最近的K个样本，预测为里面有最多类别数的类别。而KNN做回归时，一般是选择平均法，即最近的K个样本的样本输出的平均值作为回归预测值。由于两者区别不大，虽然本文主要是讲解KNN的分类方法，但思想对KNN的回归方法也适用。

 

二、KNN算法三要素

KNN算法我们主要要考虑三个重要的要素，对于固定的训练集，只要这三点确定了，算法的预测方式也就决定了。这三个最终的要素是k值的选取，距离度量的方式和分类决策规则。

　　　　对于分类决策规则，一般都是使用前面提到的多数表决法。所以我们重点是关注与k值的选择和距离的度量方式。

 

　　　　对于k值的选择，没有一个固定的经验，一般根据样本的分布，选择一个较小的值，可以通过交叉验证选择一个合适的k值。

　　　　选择较小的k值，就相当于用较小的领域中的训练实例进行预测，训练误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是泛化误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；
　　　　选择较大的k值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少泛化误差，但缺点是训练误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。
　　　　一个极端是k等于样本数m，则完全没有分类，此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单。

 　　　 1.对于距离的度量，我们有很多的距离度量方式，但是最常用的是欧式距离，即对于两个n维向量x和y，两者的欧式距离定义为：

　　　　　　　　　　

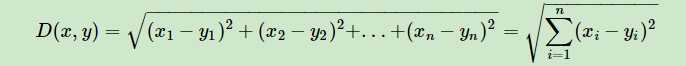
　　　　　　大多数情况下，欧式距离可以满足我们的需求，我们不需要再去操心距离的度量。

　　　　2.当然我们也可以用他的距离度量方式。比如曼哈顿距离，定义为：

　　　　　　　　　　 

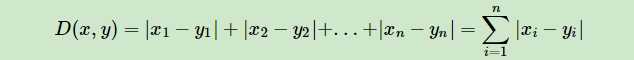
　　　　3.更加通用点，比如闵可夫斯基距离(Minkowski Distance)，定义为：

　　　　　　　　　　

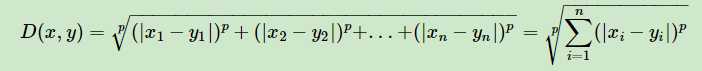
 　　　  可以看出，欧式距离是闵可夫斯基距离距离在p=2时的特例，而曼哈顿距离是p=1时的特例。

三、算法的实现(这个机器学习中的，只不过我加了自己的注释 看起来方便）

　　1.对于未知类别属性的数据集中的每个点依次执行以下操作步骤：

　　　　(1)计算已知类别数据集中的点(或者特征向量),之间的距离。

　　　　(2)按照距离递增次序排列（用argsort()排序，而不用sort()排序，argsort()是返回的是数值对应得索引，sort()返回得是数值直接排序得结果)。

　　　　(3)选取与当前点距离最小哦啊的K个点。

　　　　(4)确定前K个点所在得类别得出现频率(一般是建立一个字典，按照 {类别：出现得次数} 组合)

　　　　(5)返回前K个点出现频率最高得类别作为当前点得预测分类(一般是对保存频率的字典进行排序,用sorted()，具体用法可查官网：http://www.runoob.com/python/python-func-sorted.html）

　　　　(回归的话是返回前k个点的平均值，在这之前一般会对特征向量进行预处理，标准化或者归一化）

 

import numpy as np

datas=np.array([[1,2],[3,4],[5,6],[6,7]])  #数据，现在的数据是一个坐标
lavels=[‘A‘,‘A‘,‘B‘,‘C‘]  #种类

#K近邻分类  K-表示与当前点距离最小的K个点
def classify(X,Datas,Lavels,K):
    datasize=Datas.shpae[0]  #获取数据的维度 行数
    #距离计算
    newdatas=np.tile(X,(datasize,1))-Datas
    #tile()用来就是把数组沿各个方向复制 
    #第二个参数是方向上的复制的格式 如果是一个数，横向复制，元组的话，第一个数是纵向复制，第二个是横向复制
    
    distance=(newdatas**2).sum(axis=1)**0.05
    #对距离进行排序
    sortdistances=distances.argsort()
    #argsort()不是直接对数值进行排序，是对数值大小对应下的索引进行排序   例如[2,3,1]---[2,0,1]
    #sort()是对数值直接排序的
    
    classCount={}  #是对选取出来K个数据类别进行统计  例如{‘A’：2.‘B’：1}
    for i in range(k):
        votelavel=Lavels[sortdistances[i]]  #根据上面对数值由小到大对应的索引排序从而选择出来对应的类别
        classCount[votelavel]=classCount.get(votelavel,0)+1
        #字节的理解这样
        #classCount[‘A‘]=0   classCount.get(‘A‘)+1
    sortclasscount=sorted(classCount.items(),key=lambda k:k[1],reverse=True)  
    #sorted 可以对所有可迭代的对象进行排序操作  reverse=True  降序
    return sortclasscount[0][0]  #选取降序之后第一个频率出现最大的种类