CS184.1X 计算机图形学导论 HomeWork1

Posted 2021-01-06 keguniang

最容易填写的函数就是left。输入为旋转的角度，当前的eye与up这两个三维向量

void Transform::left(float degrees, vec3& eye, vec3& up) {

  // YOUR CODE FOR HW1 HERE

}

1.Transform是一个类，在Transform.h中可查看，类中声名了四个方法

 

2.：：

类作用域符，用法(class::name)一种从属关系

class A

{public:

    int test();}

int A::test()//表示test是属于A的

{return 0;}

3.参数

float degrees：旋转的角度

eye和up是两个三维向量

变换使用矩阵来表示，可表示为矩阵向量的乘积

 编写代码：

1>首先看rotate方法：

根据提示：Rotate仅仅根据标准的轴-角公式来建立一个旋转矩阵，使用标准的三角函数并把角度转换为弧度，简单地使用mat3 M; 来定义矩阵，所以这个方法中只是一个轴角公式的表示。

 

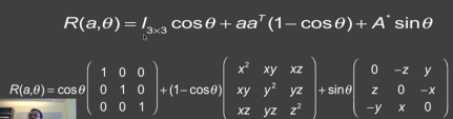
mat3 Transform::rotate(const float degrees, const vec3& axis) {

  // YOUR CODE FOR HW1 HERE

//使用标准的三角函数并把角度转换为弧度

float angle = degrees*pi / 180;

//定义矩阵,以列为主的方式存储矩阵

mat3 m1(1,0,0,

    0,1,0,

    0,0,1);

mat3 m2(axis.x*axis.x, axis.x*axis.y, axis.x*axis.z,

    axis.x*axis.y, axis.y*axis.y, axis.y*axis.z,

    axis.x*axis.z, axis.y*axis.z, axis.z*axis.z);

mat3 m3(0, axis.z,-axis.y,

        -axis.z,0, axis.x,

    axis.y,-axis.x,0);

mat3 result;

result = cos(angle) * m1 + (1-cos(angle))*m2 + sin(angle)*m3;

  // You will change this return call

   return result;

}

2>再看left方法：

输入为旋转的角度，当前的eye与up这两个三维向量。注意你可能需要把度数转换为弧度来建立一个旋转矩阵（标准形式下）。你的任务是当用户向左移时，正确地更新eye和up向量.

3>Up

up函数稍稍复杂一些，但和left有一样的基本需求。你可能需要使用一些辅助函数，比如glm::cross 和辅助向量。同样的，你需要正确地更新eye和up向量

4>lookAt

最后，你需要根据eye和up向量编写代码计算变换矩阵。你可能需要回顾一下课程视频，特别是gluLookAat 的推导来完成这个工作。你可以定义一个u v w 坐标系（作为一个3维向量），建立一个辅助的4x4矩阵M 作为这个函数的结果返回。