题目分享I 三代目

Posted 2020-12-23 lin4xu

题意：

波雷卡普和瓦西里喜欢简单的逻辑游戏。今天他们玩了一个游戏，这个游戏在一个很大的棋盘上进行，他们每个人有一个棋子。他们轮流移动自己的棋子，波雷卡普先开始。每一步移动中，波雷卡普可以将他的棋子从(x,y) 移动到 (x-1,y) 或者 (x,y-1)。而瓦西里可以将他的棋子从(x,y) 移动到 (x-1,y),(x-1,y-1) 或者 (x,y-1)。当然他们可以选择不移动。

还有一些其它的限制，他们不能把棋子移动到x或y为负的座标，或者移动到已经被对手占据的座标。最先到达（0，0）的人获胜。

现在给定他们棋子的座标，判断一下谁会获胜

分析：

设A为先手，B为后手，

显然可以大致分为以下三种形式，分别是

Ax>=Bx && Ay>=By

 

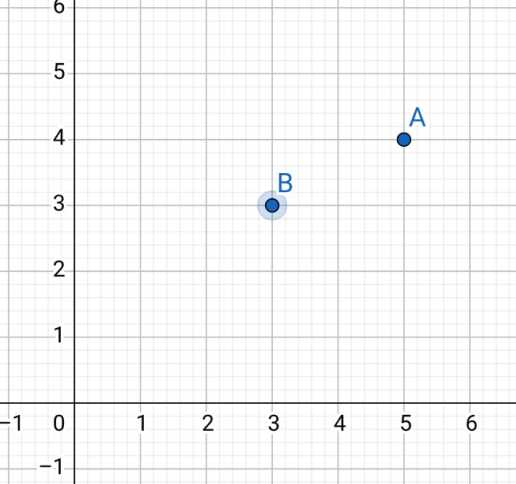
 Ax>Bx && Ay<By

 

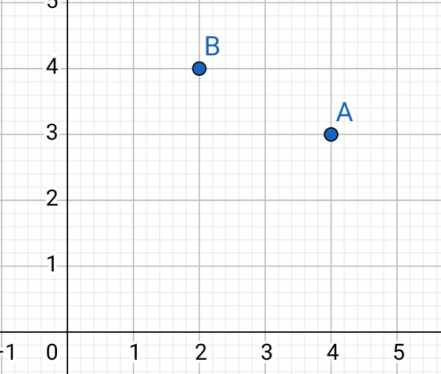
 Ax<=Bx && Ay<=By

 

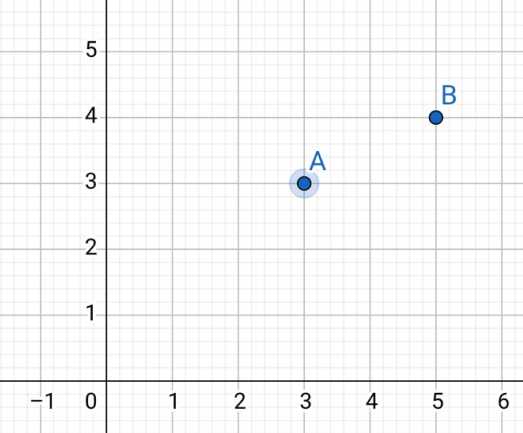
 其中Ax<Bx &&Ay>By 可以并在形式2中

对于形式3来说

A可以选择一直向下走，一旦B往左移，那A就往左走，因为A到达y轴一定比B快，所以B就会被A困死

如果B往下移，那A还往下移，具体就是这样

 

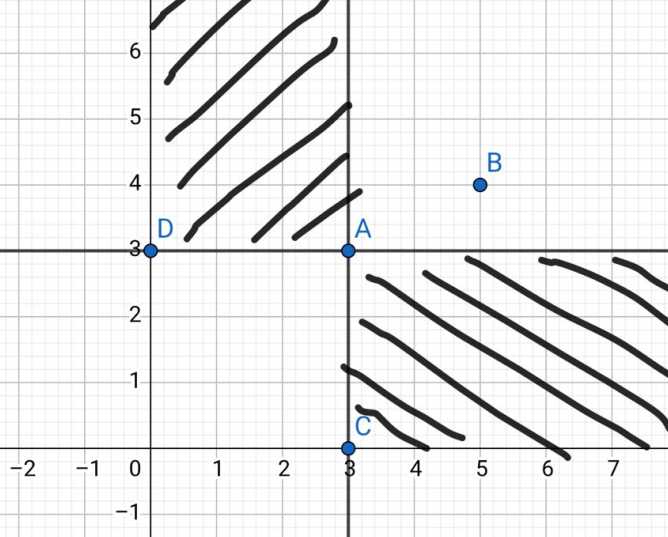
 当B走入///阴影区时，A就往左走直至封住B，

当B走入\\阴影区时，A就往下走直至封住B

剩下的A就慢慢走即可

也就是说当Ax≤Bx && Ay≤By 时 A胜

对于形式2来说

这就有些难判断B是否能够拦截A

把A的路径画出

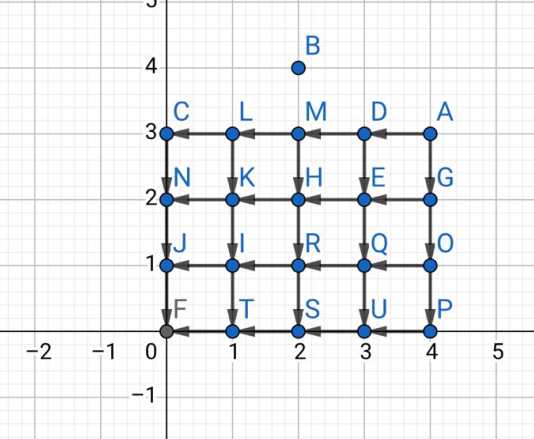
 再把B的也画上

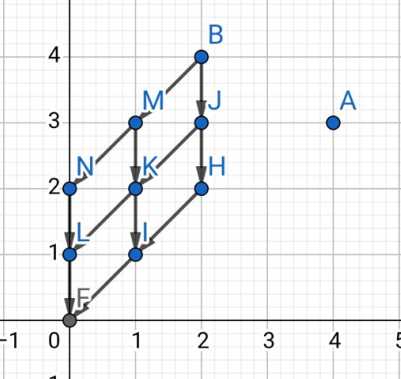
显然，在没有拦截的情况下，B走的步数是max(Bx,By)，A走的步数是Ax+Ay

如果A走的步数≤B走的步数，那么显然B就需要想办法拦截A

如果B在(x,y)处拦截A，也就是比A要先走到A想走的地方，使A无法走最短路

B需要的时间是max(Bx-x,By-y) A需要的时间是Ax+Ay-x-y

因为Ax+Ay≤max(Bx,By)

所以Ax+Ay-x-y≤max(Bx,By)-x-y=max(Bx-x-y,By-x-y)≤max(Bx-x,By-y)也就是B走的时间

也就是说A一定会走在B前面，也就是B不可能拦截A

如果反过来也是一样的

所以，当Ax+Ay≤max(Bx,By)时，先手胜，否则后手胜

对于形式1来说，其实与形式3又大同小异，

所以综上就是，

if Ax<=Bx且Ay<=By时 A胜

else if Ax>=Bx且Ay>=By时 B胜

else if Ax+Ay≤max(Bx,By)  A胜

else B胜

稍微合并一下即可得到代码

代码：

#include<cstdio>
#include<algorithm>
using namespace std;

int main()
{
    int a,b,c,d;
    scanf("%d%d%d%d",&a,&b,&c,&d);
    if(a<=c&&b<=d||a+b<=max(c,d)) printf("Polycarp");
    else printf("Vasiliy");
    return 0;
}