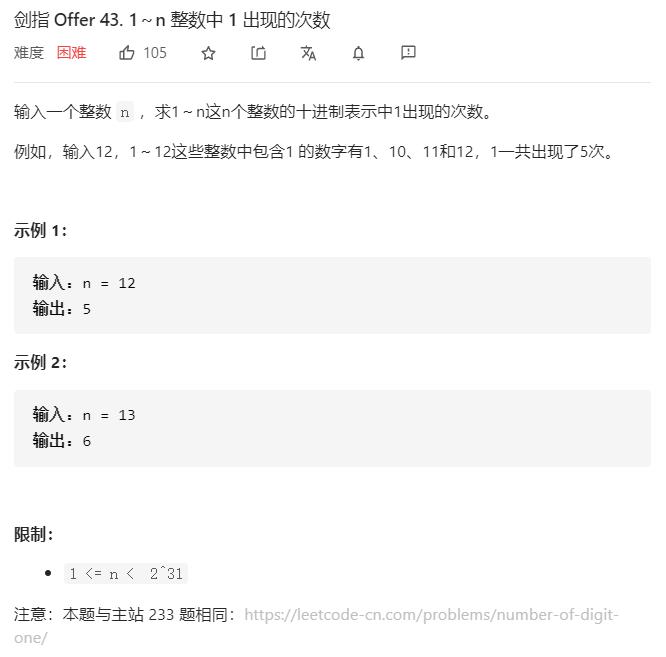
剑指 Offer 43. 1～n 整数中 1 出现的次数

Posted 2020-12-21 fengzeng666

 

思路

这题如果直接用暴力法，1~n逐一判断，每个数逐位判断需要O(L)的时间，其中L为n的位数，所以总的时间复杂度为O(L*n)，这显然会超时。

方法：模拟

首先计算n的总位数len，假设n是4位数abcd, x=n=abcd

对于n中的个位数d：
如果d ≥ 1，对于1~n中个位数为1的数，则其他3位数可以为000~abc，共1+abc种情况，即(000~abc)1；
如果d = 0, 对于1~n中个位数为1的数，则其他3位数可以为000~abc-1，共1+abc-1种情况，即(000~abc-1)1.

对于n中的十位数c，其右边有2位数cd，
如果c>1，对于1~n中十位数为1的数，其他3位数可以是000~ab9,共有1+ab9种情况，即该数可以为(00~ab)1(0~9)；
如果c=1，对于1~n中十位数为1的数，其他3位数可以是000~abd,共有1+acd种情况，即该数可以为(00~ab)1(0~d)；
如果c=0，对于1~n中十位数为1的数，其他3位数可以是000~(a-1)cd,共有1+(a-1)cd种情况，即该数可以为(00~ab-1)1(0~9)

百位，千位，万位等其他位依此类推。可以依此法编写代码。

 

举例：

    拿21058举个例子，从右往左逐位分析：

    对于第5位8：

        对于1~n中第5位数为1的数，左边的四位可以是0000~2105，共有2106种情况，即该数可以为(0~2105)1

    对于第4位5：

        对于1~n中第4位数为1的数，剩余的四位可以是0000~2109，共有2110种情况，即该数可以为(0~210)1(0~9)

    对于第3位0：

        对于1~n中第3位数为1的数，剩余的四位可以是0000~2099，共有2100种情况，即该数可以为(00~20)1(00~99)

    对于第2位1：

        对于1~n中第2位数为1的数，剩余的四位可以是0000~2058，共有2059种情况，即该数可以为(0~2)1(000~058)

    对于第1位2：

        对于1~n中第1位数为1的数，剩余的四位可以是0000~9999，共有10000种情况，即该数可以为1(0000~9999)

    因此，共有2106+2110+2100+2059+10000 = 18375种情况。

 

注意：这种方法并没有漏算，比如110中有两个1，当判断到第2位的时候，第1位的1被算进去了，判断到第1位的时候，第2位的1也被算进去了，所以110中计算了两种情况，这和题目是相符的。

复杂度分析

时间复杂度：O(L²)，其中L为数字n的长度(位数)

空间复杂度：O(1)

 

 1 class Solution {
 2 public:
 3     int countDigitOne(int n) {
 4         int res = 0;
 5         int x = n;
 6         
 7         //首先计算n的总位数len
 8         int len = 0;
 9         while(x) {
10             len++;
11             x /= 10;
12         }
13 
14         x = n;  // 假设n是4位数abcd, x=n=abcd
15         
16         for(int i = len; i >= 1; --i) {
17             int m = x % 10; //m为当前第i位数的值
18             x /= 10;        //x为当前第i位的左侧数字的大小(也就是n的前i位数的大小)
19             if(i == len) {
20                 if(m >= 1) {
21                     res += 1 + x;
22                 } else {
23                     res += 1 + (x-1);
24                 }
25             } else {
26                 if(m > 1) {
27                     int rightDigitNum = len-i;
28                     int t = x;
29                     for(int j = 1; j <= rightDigitNum; ++j) {
30                         t = t*10 + 9;
31                     }
32 
33                     res += 1 + t;
34                 } else if(m == 1) {
35                     int t = x;
36                     int r = 1;
37                     int rightDigitNum = len-i;
38                     for(int j = 1; j <= rightDigitNum; ++j) {
39                         r *= 10;
40                         t *= 10;
41                     }
42 
43                     //n % r表示当前位右侧数字的大小
44                     //最终算出来的t表示数字n去掉第i位数之后，剩余的数字的大小
45                     t +=  n % r;    
46                     res += 1 + t;
47 
48                 } else {    // m == 0
49                     int rightDigitNum = len-i;
50                     int t = x-1;
51                     for(int j = 1; j <= rightDigitNum; ++j) {
52                         t = t*10 + 9;
53                     }
54 
55                     res += 1 + t;
56 
57                 }
58             }
59         }
60         return res;
61     }
62 
63 };