棋盘覆盖问题（分治）

Posted 2020-12-20 pdream

一个骨牌为3格。

当棋盘边长为2，总格数(2^2-1)/3,发现可以整除。

那么因为棋盘边长为2^k，总格数(2^4-1)/3,可以用n^2-1=(n+1)(n-1)拆开，利用上一步，发现可以整除。

可以证的无论棋盘的边长，都可以在有一个奇异点的情况下被整除。

那么我们的目标是把大的棋盘一步步拆成边长为2的小棋盘，其中的奇异点可以是一个普通骨牌当成成三个奇异点用。

最后的步骤：

1、大棋盘拆四个象限，在没有奇异点的象限，棋盘中间填一个骨牌。

2、进入各个小象限，上一步的骨牌当作奇异点，继续重复以上步骤/

3、最后会变成边长为2的情况，一个奇异点和三个被骨牌填的格子。

 

 

 

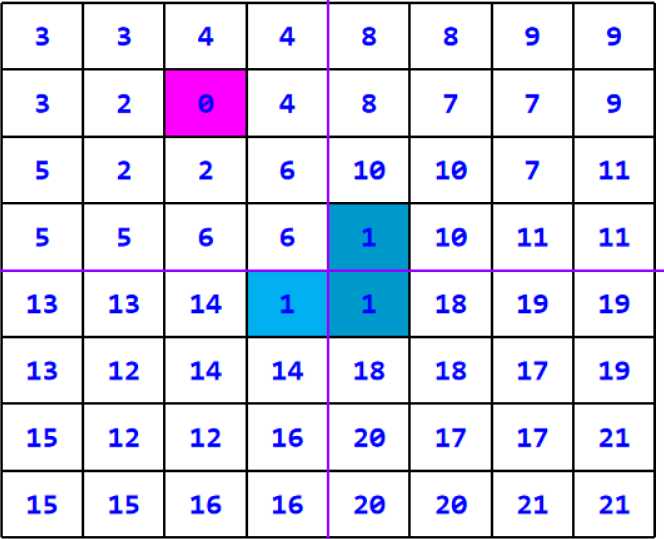
void ChessBoard(int tr,int tc,int dr,int dc,int size){//tr，tc为当前象限左上角，dr、dc为奇异点所在，size记录棋盘大小
    if(size==1) return;
    int t=tile++;
    int s=size/2;
    //左上角象限
    if(dr<tr+s && dc<tc+s)//有奇异点 
        ChessBoard(tr, tc,dr,dc,s);
    else{ 
        board[tr+s-1][tc+s-1]=t; //用t号型骨牌填右下角，当作奇异点 
        ChessBoard(tr,tc,tr+s-1,tc+s-1,s);//有了奇异点，继续处理 
    //考虑右上角象限
    if(dr<tr+s && dc>=tc+s)
        ChessBoard(tr, tc+s,dr,dc,s);
    else{
        board[tr+s-1][tc+s]=t; 
        ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
    }
    //处理左下角象限
    if(dr>=tr+s && dc<tc+s) 
        ChessBoard(tr+S, tc,dr,dc,s);
    else{ 
        board[tr+s][tc+s-1]=t; 
        ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
    }
    //处理右下角象限 
    if(dr>=tr+s && dc>=tc+s) 
        ChessBoard(tr+s,tc+s ,dr,dc,s);
    else{
        board[tr+s][tc+s]=t;
        ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
    }
}