经典算法之棋盘覆盖问题 --分治法

Posted 2023-01-02 FreeeLinux

一：算法分析

棋盘覆盖问题要求在2^k * 2^k 个方格组成的棋盘中，你给定任意一个特殊点，用一种方案实现对除该特殊点的棋盘实现全覆盖。

建立模型如图：

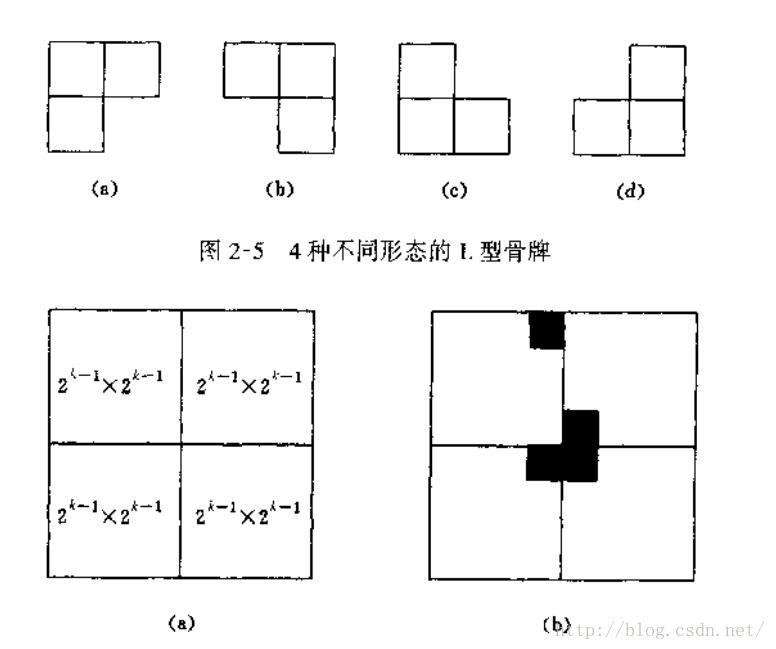
解决方案就是利用分治法，将方形棋盘分成4部分，如果该特殊点在某一部分，我们就去递归他，如果不在某一部分，我们假设一个点为特殊点，同样递归下去，知道全覆盖。

    左上角的子棋盘（若不存在特殊方格）：则将该子棋盘右下角的那个方格假设为特殊方格；

    右上角的子棋盘（若不存在特殊方格）：则将该子棋盘左下角的那个方格假设为特殊方格；

    左下角的子棋盘（若不存在特殊方格）：则将该子棋盘右上角的那个方格假设为特殊方格；

    右下角的子棋盘（若不存在特殊方格）：则将该子棋盘左上角的那个方格假设为特殊方格；

更详细的递归覆盖过程参见此文档，有步骤化的PPT图片展示：点击打开链接

二：代码如下

</pre><pre class="cpp" name="code">#include <iostream>
using namespace std;

const int BOARD_SZ = 8;
static int tile = 1;
static int board[BOARD_SZ][BOARD_SZ] = 0;

void chess_board(int tr, int tc, int dr, int dc, int size)

    if(size == 1)
        return;

    int t = tile++;   //tile means 瓦片，基石，覆盖的步骤
    int sz = size / 2;    //每次进行划分

    //cover top left corner
    if(dr < tr+sz && dc < tc+sz)     //notice < <   //注意一共四种情况，<>=这几个符号要控制好边界
        chess_board(tr, tc, dr, dc, sz);
    else
        board[tr+sz-1][tc+sz-1] = t;
        chess_board(tr, tc, tr+sz-1, tc+sz-1, sz);
    

    //cover top right corner
    if(dr < tr+sz && dc >= tc+sz)   //notice < >=
        chess_board(tr, tc+sz, dr, dc, sz);
    else
        board[tr+sz-1][tc+sz] = t;
        chess_board(tr, tc+sz, tr+sz-1, tc+sz, sz);
    

    //cover lower left corner
    if(dr >= tr+sz && dc < tc+sz)   //notice >= <
        chess_board(tr+sz, tc, dr, dc, sz);
    else
        board[tr+sz][tc+sz-1] = t;
        chess_board(tr+sz, tc, tr+sz, tc+sz-1, sz);
    

    //cover lower right corner
    if(dr >= tr+sz && dc >= tc+sz)  //notice >= >=
        chess_board(tr+sz, tc+sz, dr, dc, sz);
    else
        board[tr+sz][tc+sz] = t;                       //标记一个假设的特殊点
        chess_board(tr+sz, tc+sz, tr+sz, tc+sz, sz);   //递归该部分
    


void print_chess_board()

    cout.setf(ios::left);     //左对齐
    for(int i=0; i<BOARD_SZ; ++i)
        for(int j=0; j<BOARD_SZ; ++j)
            cout.width(3);    //打印宽度为3
            cout<<board[i][j];
        
        cout<<endl;
    


int main()

    chess_board(0, 0, 3, 4, BOARD_SZ);
    print_chess_board();
    return 0;

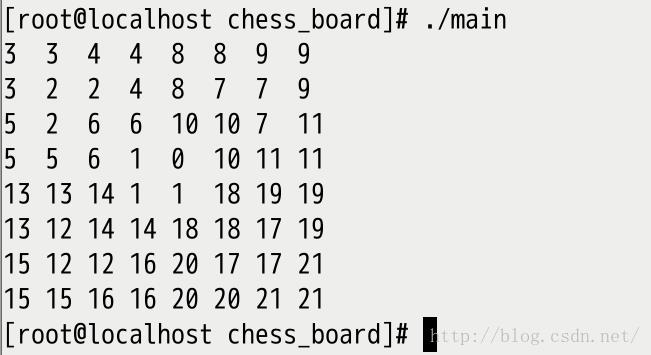
结果如图：