棋盘覆盖问题——分治法
Posted Oo名字不好取oO
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了棋盘覆盖问题——分治法相关的知识，希望对你有一定的参考价值。
问题描述
有一个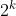 
x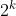 （k>0）的棋盘，恰好有一个方格与其他方格不同，称之为特殊方格。现在要用如下图所示的L形骨牌覆盖除了特殊方格以外的其他全部方格，骨牌可以任意旋转，并且任何两个骨牌不能重复。请给出一种覆盖方式。
样例：
输入：
输出：
思路——分治法：
将一个规模为n的问题分解为k个规模较小的子问题，这些子问题相互独立且与原问题相同。
递归地解决这些子问题，然后将各个子问题的解合并得到原问题的解。
就是将规模为n的问题自顶向下分解，直到小问题分解到足够小，可以解决时，再自底向上合并，从而得到原来的解。
当k=0（棋盘只有1格），特殊点只能唯一，L骨牌数为0
当k >0，则可将 2*kⅹ2*k 棋盘分割为 4个 2*k-1ⅹ2*k-1 的子棋盘
判断特殊点在哪一个子棋盘中，用一块L骨牌放在其它三个子棋盘的连接处
以此类推，则最后可将每个子棋盘划分为1格的棋盘，结束递归
代码实现：
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int arr[1000][1000]; int num = 0; void ChessBoard(int x, int y, int a, int b, int length); int main() //棋盘大小 int length; cout << "请输入length：" ; cin >> length; //空白点坐标 int a, b; cout << "请输入空格位置："; cin >> a >> b; cout << endl; arr[a][b] = 0;//标点用0表示 ChessBoard(1, 1, a, b, length); for (int i = 1; i <= length; i++) for (int j = 1; j <= length; j++) cout << arr[i][j] << " "; cout << endl; return 0; void ChessBoard(int x, int y, int a, int b, int length) if (length == 1) return; int h = length / 2;//分割棋盘 int t = ++num;//骨牌号，从1开始,相同数字代表是同一块 //以“田”的左下角为（1,1） //左下角 if (a < x + h && b < y + h) ChessBoard(x, y, a, b, h); else arr[x + h - 1][y + h - 1] = t; ChessBoard(x, y, x + h - 1, y + h - 1, h); //左上角 if (a < x + h && b >= y + h) ChessBoard(x, y + h, a, b, h); else arr[x + h - 1][y + h] = t; ChessBoard(x, y + h, x + h - 1, y + h, h); //右下角 if (a >= x + h && b < y + h) ChessBoard(x + h, y, a, b, h); else arr[x + h][y + h - 1] = t; ChessBoard(x + h, y, x + h, y + h - 1, h); //右上角 if (a >= x + h && b >= y + h) ChessBoard(x + h, y + h, a, b, h); else arr[x + h][y + h] = t; ChessBoard(x + h, y + h, x + h, y + h, h);
参考资料：《计算机算法设计与分析（第四版）》
棋盘覆盖问题——分治法——代码清晰易懂
一、运行环境
DevC++
二、题目描述
棋盘覆盖问题。有一个2^k × 2^k个方格的棋盘，其中恰有一个方格残缺。用下面四种三格板覆盖更大的棋盘。
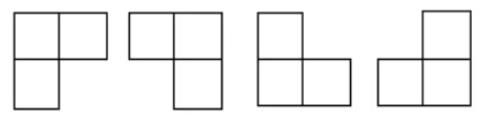
要求：
①两个三格板不能重叠。
②三格板不能覆盖残缺方格，但必须覆盖其他所有的方格。
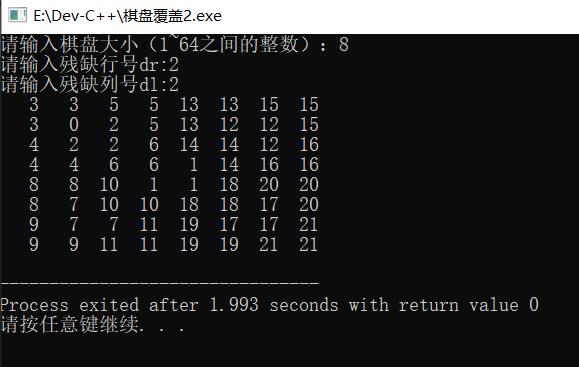
用以下形式进行结果输出
三、问题分析
采用分治的方法解决该问题。把2k×2k的棋盘分为4个2k-1×2k-1的子棋盘，使问题规模变小，直至将棋盘分割为1×1的子棋盘。
该问题属于二分法不相似的情况：分割后的4个子棋盘只有一个带有残缺。分治的技巧在于如何划分棋盘，使划分后的子棋盘的大小相同，并且每个子棋盘均包含一个残缺方格，从而将原问题分解为规模较小的棋盘覆盖问题。k>0时，可将2k×2k的棋盘划分为4个2k-1×2k-1的子棋盘。这样划分后，由于原棋盘只有一个残缺方格，所以，这4个子棋盘中只有一个子棋盘包含该残缺方格，其余3个子棋盘中没有残缺方格。为了将这3个没有特殊方格的子棋盘转化为残缺棋盘，以便采用递归方法求解，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种划分策略，直至将棋盘分割为1×1的子棋盘。
四、算法设计
1. 怎样表示一个棋盘
三要素：棋盘左上角的横坐标、纵坐标、棋盘边长
2.存储结构设计
（1）需要有一个二维数组来标记棋盘，设为全局变量，从i=1,j=1开始储存标记
（2）L型的位置，需要用“111”、“222”…“nnn”来标记，这就需要设置一个计数的变量，每次递归让这个计数变量自加1
3. 递归设计
整体来说，是进行一个深度优先的遍历：
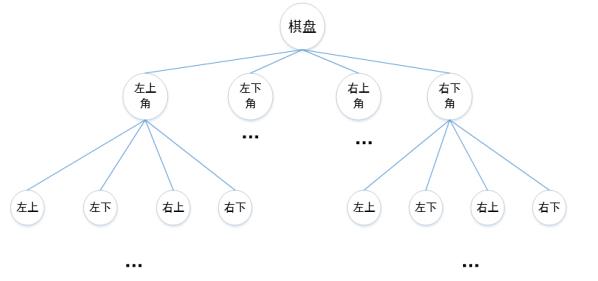
4. 一次递归的设计
于一整个棋盘来说，残缺的位置分为4种情况：
①残缺在左上角子棋盘中
②残缺在右上角子棋盘中
③残缺在左下角子棋盘中
④残缺在右下角子棋盘中
对于每一个子棋盘，分为两种情况：
①残缺在子棋盘内，不需要用L型覆盖一个格子
②残缺不在子棋盘内，需要用L型覆盖一个格子
对于一整个棋盘来说，残缺的位置分为4种情况，这就需要用到4个if语句。
对于每一个子棋盘，分为两种情况，这就需要上述的4个if语句中都具备一个else分支。
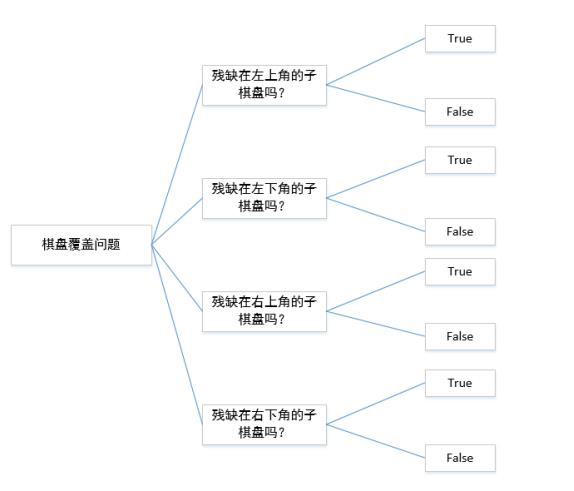
五、代码
#include <stdio.h>
int chess[65][65]={0};
//从chess[1][1]开始存放
static int t=0;
int m;
void cover(int a,int b,int dr,int dl,int length);
int main(){
int n,a,b,dr,dl,length;
//a,b是子棋盘左上角的行号和列号
//dr，dl是特殊点的行号和列号
//length是棋盘宽度
printf("请输入棋盘大小（1~64之间的整数）：");
scanf("%d",&length);
printf("请输入残缺行号dr:");
scanf("%d",&dr);
printf("请输入残缺列号dl:");
scanf("%d",&dl);
a=b=1;
m=length;
cover(a,b,dr,dl,length);
for(int i=1;i<=m;i++){ //输出结果,都从1号开始存放的
for(int j=1;j<=m;j++){
printf("%4d",chess[i][j]);
if(j==m){
printf("\\n");
}
}
}
}
void cover(int a,int b,int dr,int dl,int length){
for(int i=1;i<=m;i++){ //输出结果,都从1号开始存放的
for(int j=1;j<=m;j++){
printf("%4d",chess[i][j]);
if(j==m){
printf("\\n");
}
}
}
printf("------------\\n");
if(length==1){
return;
}
t++;
int L =t;
int l=length/2;
if(dr<a+l && dl<b+l){ //残缺在左上角
cover(a,b,dr,dl,l);
}
else{ //残缺不在左上角，填充一个方格
chess[a+l-1][b+l-1]=L;
cover(a,b,a+l-1,b+l-1,l);
}
if(dr>=a+l && dl<b+l){//残缺在左下角
cover(a+l,b,dr,dl,l);
}
else{ //残缺不在左下角，填充一个方格
chess[a+l][b+l-1]=L;
cover(a+l,b,a+l,b+l-1,l);
}
if(dr<a+l && dl>=b+l){//残缺在右上角
cover(a,b+l,dr,dl,l);
}
else{ //残缺不在右上角，填充一个方格
chess[a+l-1][b+l]=L;
cover(a,b+l,a+l-1,b+l,l);
}
if(dr>=a+l && dl>=b+l){//残缺在右下角
cover(a+l,b+l,dr,dl,l);
}
else{ //残缺不在右下角，填充一个方格
chess[a+l][b+l]=L;
cover(a+l,b+l,a+l,b+l,l);
}
}
下面的版本二是写给我自己看的，和上面的原理一模一样
#include<bits/stdc++.h>
using namespace std;
/*
为了方便逻辑判断，棋盘的行和列都从1开始
不需要将原始的残缺块位置设为全局变量，因为后来的填充都要看作残差块
*/
int board[65][65]; //int型全局变量默认为0
int N; //棋盘的边长
int cnt=0; //记录该摆放第几块骨牌了
void cover(int dr, int dl, int a, int b, int length){
//每一次递归都需要知道五个参数：残缺的行，残缺的列，子棋盘左上角的行，左上角的列，子棋盘边长
int l=length/2;
cnt++;
int L=cnt;
if(length==1){ //递归出口
return;
}
//如果残差块在左上角的子棋盘中
if(dr<=a+l-1&&dl<=b+l-1){
cover(dr,dl,a,b,length/2);
}
else{ //不在的话，把右下角格子的填充上
board[a+l-1][b+l-1]=L;
cover(a+l-1,b+l-1,a,b,length/2);
}
//如果残差块在右上角的子棋盘中
if(dr<=a+l-1&&dl>=b+l){
cover(dr,dl,a,b+l,length/2);
}
else{ //不在的话，把左下角格子的填充上
board[a+l-1][b+l]=L;
cover(a+l-1,b+l,a,b+l,length/2);
}
//如果残差块在左下角的子棋盘中
if(dr>=a+l&&dl<=b+l-1){
cover(dr,dl,a+l,b,length/2);
}
else{ //不在的话，把右上角格子的填充上
board[a+l][b+l-1]=L;
cover(a+l,b+l-1,a+l,b,length/2);
}
//如果残差块在右下角的子棋盘中
if(dr>=a+l&&dl>=b+l){
cover(dr,dl,a+l,b+l,length/2);
}
else{ //不在的话，把左上角格子的填充上
board[a+l][b+l]=L;
cover(a+l,b+l,a+l,b+l,length/2);
}
}
int main(){
int dr; //残缺所在的行数
int dl; //残缺所在的列数
printf("请输入棋盘大小（1~64之间的整数）：");
scanf("%d",&N);
printf("请输入残缺行号dr:");
scanf("%d",&dr);
printf("请输入残缺列号dl:");
scanf("%d",&dl);
cover(dr,dl,1,1,N);
/*---打印输出-----*/
for(int i=1;i<=N;i++){ //输出结果,都从1号开始存放的
for(int j=1;j<=N;j++){
printf("%4d",board[i][j]);
if(j==N){
printf("\\n");
}
}
}
return 0;
}
六、常见错误分析
在写版本二时，出现了各种错误。列举如下
（1）没有3个相同的序号连在一起
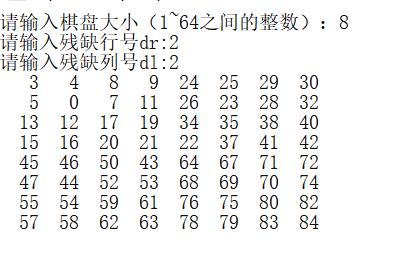
错误代码（局部）如下：
int l=length/2;
cnt++;//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
if(length==1){
return;
}
if(dr<=a+l-1&&dl<=b+l-1){
cover(dr,dl,a,b,length/2);
}
else{
board[a+l-1][b+l-1]=cnt;//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
cnt++;
cover(a+l-1,b+l-1,a,b,length/2);
}
原因在于，计数器cnt是全局变量，随着递归的深入，cnt的值不断加1，回溯时也没有减1，这就导致递归树上同一层次的结点的cnt不同。
解决方法是，在递归函数内新定义一个局部计数器L,用L去给每一个分支赋值。
cnt++;
int L=cnt; //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
if(length==1){
return;
}
if(dr<=a+l-1&&dl<=b+l-1){
cover(dr,dl,a,b,length/2);
}
else{
board[a+l-1][b+l-1]=L; //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
cover(a+l-1,b+l-1,a,b,length/2);
}
（2）上面的问题解决了（存在3个相同的序号连在一起了），但序号不连续
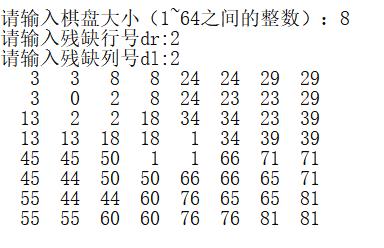
这个错误很难发现！原因在于下面两行代码的顺序。
cnt++;
int L=cnt;
if(length==1){ //递归出口
return;
}
按照上面这样写，进入递归出口前会使得计数器加1，但是进入递归出口根本不需要加1，这也就使得序号出现间断。
解决方法很简单，就是把计数器加一的代码移到递归出口的下面
if(length==1){ //递归出口
return;
}
cnt++;
int L=cnt;
以上是关于棋盘覆盖问题——分治法的主要内容，如果未能解决你的问题，请参考以下文章