LCA在线算法详解

Posted 2020-10-01

LCA（最近公共祖先）的求法有多种，这里先介绍第一种：在线算法。

声明一下：下面的内容参考了http://www.cnblogs.com/scau20110726/archive/2013/05/26/3100812.html。

 

在线算法就是利用了DFS和RMQ两种算法，它先是预处理好所有情况，然后根据输入输出答案，在输入比较多的时候用比较好。

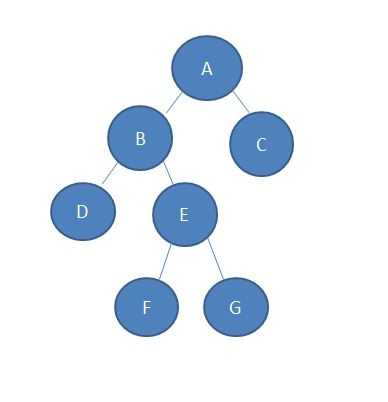
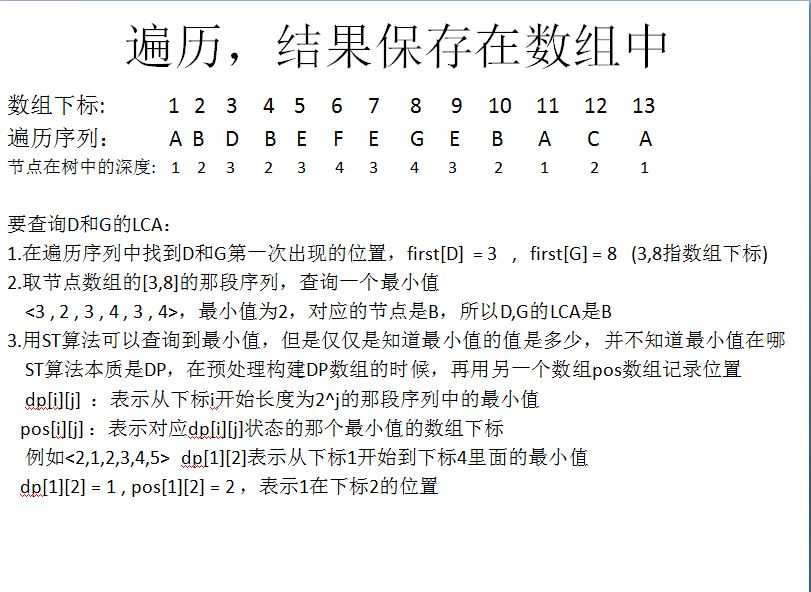
上面两张图介绍了在线算法的做法，要理解并不难，下面附上实现代码：

 1 /*******************************
 2 dfs实现代码
 3 *******************************/
 4 
 5 void dfs(int u, int dep)
 6 {
 7     vis[u]=1;
 8     ver[++tot]=u;   //遍历序列
 9     first[u]=tot;   //结点第一次出现位置
10     deep[tot]=dep;     //深度
11     for(int i=head[u];i!=-1;i=e[i].next)
12     {
13         if(!vis[e[i].v])
14         {
15             int v=e[i].v, w=e[i].w;
16             dfs(v,dep+1);
17             ver[++tot]=u;      //回溯
18             deep[tot]=dep;
19         }
20     }
21 }

 

接下来是ST算法，也就是RMQ，计算出所有的d[i][j]。

 1 void ST(int n)
 2 {
 3     for(int i=1;i<=n;i++)  dp[i][0]=i;
 4     for(int j=1;(1<<j)<=n;j++)
 5         for(int i=1;i+(1<<j)-1<=n;i++)
 6         {
 7             int a=dp[i][j-1],b=dp[i+(1<<(j-1))][j-1];
 8             dp[i][j]=deep[a]<deep[b]?a:b;
 9         }
10 }

 

最后是LCA的查询部分，其实也属于RMQ。

1 int LCA(int u, int v)
2 {
3     int x=first[u], y=first[v];   //查找出他最先出现的地方
4     if(x>y)  swap(x,y);
5     int res=RMQ(x,y);    //查询出的是他祖先的下标
6     return ver[res];   
7 }