LCA 在线离线算法 笔记

Posted 2020-10-09 为了更优秀的你，加油！

参考链接：

http://dongxicheng.org/structure/lca-rmq/

http://blog.csdn.net/y990041769/article/details/40887469

http://www.cnblogs.com/JVxie/p/4854719.html

http://m.blog.csdn.net/qq_35935435/article/details/54916022

Tarjan离线算法：

什么是Tarjan(离线)算法呢？顾名思义，就是在一次遍历中把所有询问一次性解决，所以其时间复杂度是O(n+q)。

　　　　Tarjan算法的优点在于相对稳定，时间复杂度也比较居中，也很容易理解。

　　　　下面详细介绍一下Tarjan算法的基本思路：

　　　　　　1.任选一个点为根节点，从根节点开始。

　　　　　　2.遍历该点u所有子节点v，并标记这些子节点v已被访问过。

　　　　　　3.若是v还有子节点，返回2，否则下一步。

　　　　　　4.合并v到u上。

　　　　　　5.寻找与当前点u有询问关系的点v。

　　　　　　6.若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

　　　　遍历的话需要用到dfs来遍历，合并就是利用并查集来合并两个节点。

　　　　伪代码如下：　　

Tarjan(u)//marge和find为并查集合并函数和查找函数
{
    for each(u,v)    //访问所有u子节点v
    {
        Tarjan(v);        //继续往下遍历
        marge(u,v);    //合并v到u上
        标记v被访问过;
    }
    for each(u,e)    //访问所有和u有询问关系的e
    {
        如果e被访问过;
        u,e的最近公共祖先为find(e);
    }
}

RMQ区间最值询问算法：ST（Sparse Table）算法是一个非常有名的在线处理RMQ问题的算法，它可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询。

在线算法（DFS+ST） 
①DFS 
举个例子。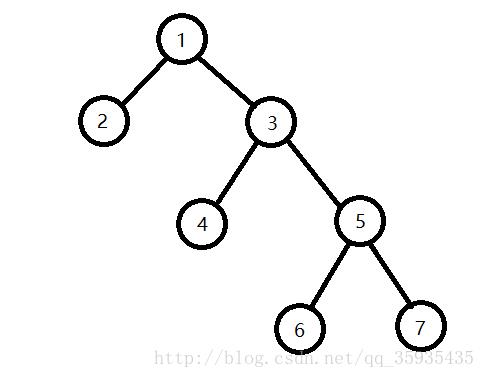 
 
假设遍历顺序从右至左，则DFS遍历可得。 
DFS遍历序列F_____________1 3 5 7 5 6 5 3 4 3 1 2 
深度序列deep______________1 2 3 4 3 4 3 2 3 2 1 2 
结点首次出现位置first ______1 12 2 9 3 6 4 
对于查询两个结点的LCA就是各自首次出现位置间深度最小的结点。于是可以转化为RMQ问题，在一段区间中寻找最小值。所以再用ST算法解决该问题。 
根据例题，如果询问LCA(4,7)，就相当于RMQ(4,7)。first[4]=9，first[7]=4。在深度序列中区间(4,9)是4 3 4 3 2 3，而最近公共祖先的深度就是这段区间中最小的2。再将深度代入遍历序列得到LCA(4,7)=3。 
②ST 
令F[i,j]为从下标i开始，长度为2^j的元素的最小值。那么状态转移方程就是F[i,j]=min(F[i,j-1],F[i+2^(j-1),j-1])。 
③查询 
假如要查询[m,n]的最小值，那么先求出一个最大的k。使k满足2^k<=(n-m+1)。于是我们可以将[m,n]分成两个（部分重叠的）长度为2^k的区间:[m,m+2^k-1],[n-2^k+1,n];F[m,k]为F[m,m+2^k-1]的最小值，F[n-2^k+1,k]是[n-2^k+1,n]的最小值。状态转移方程：RMQ(i,j)=min(F[m,k],F[n-2^k+1,k]); 
接下来看一下例题&代码。

LZOI2225 最近公共祖先

题目描述 
如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。 
输入 
第一行包含三个正整数n, q, s，分别表示树的结点个数、询问的个数和树根结点的序号。 
接下来n - 1行每行包含两个正整数u, v，表示u结点和v结点只见有一条直接连接的边（数据保证可以构成树）。 
接下来q行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。 
输出 
输出包含q行，每行包含一个正整数，依次为每一个询问的结果。

#include<iostream>
using namespace std;
int n,q,root,u,v,a,b,F[50001],f[50001][21],first[50001],deep[50001],head[50001],tot;
bool vis[50001];
struct E
{
    int v;
    int u;
    E(){u=0;}
}e[1000001];
int en=0;
void dfs(int u,int dep)
{
    vis[u]=1;
    F[++tot]=u;
    first[u]=tot;
    deep[tot]=dep;
    for(int i=head[u];i!=0;i=e[i].u)
        if(!vis[e[i].v])
        {
            dfs(e[i].v,dep+1);
            F[++tot]=u;
            deep[tot]=dep;
        }
}
void ST(int len)
{
    for(int i=1;i<=len;i++)f[i][0]=i;
    for(int j=1;(1<<j)<=len;j++)
    {
        for(int i=1;i+(1<<j)-1<=len;i++)
        {
            int a=f[i][j-1],b=f[i+(1<<(j-1))][j-1];
            f[i][j]=deep[a]<deep[b]?a:b;
        }
    }
}
int RMQ(int l,int r)
{
    int k=0;
    while((1<<(k+1))<r-l+1)k++;
    int a=f[l][k],b=f[r-(1<<k)+1][k];
    return deep[a]<deep[b]?a:b;
}
int LCA(int u,int v)
{
    int x=first[u],y=first[v];
    if(x>y)swap(x,y);
    int res=RMQ(x,y);
    return F[res];
}
void add(int u,int v)//这里用到了邻接表存储哦！
{
    en++;
    e[en].v=v;
    e[en].u=head[u];
    head[u]=en;
}
int main()
{
    cin>>n>>q>>root;
    for(int i=1;i<n;i++)
    {
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    dfs(root,1);
    ST(tot);
    for(int i=1;i<=q;i++)
    {
        cin>>a>>b;
        cout<<LCA(a,b)<<endl;
    }
    return 0;
}