51nod-1138连续整数的和

Posted 2020-12-05 lesroad

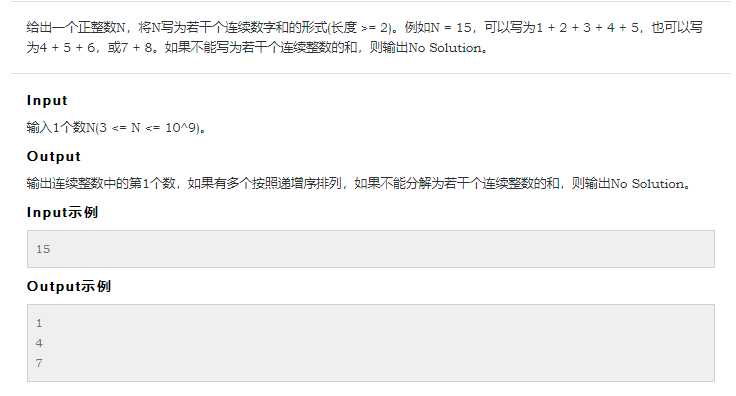
本来想着用尺取的思想，不过会超时。利用等差数列S = na+n*n(n-1)/2,得a = (2*S-n*(n-1))/(2*n),然后遍历n，只要满足a是整数就可以，这样复杂度从O（S）变成了O（sqrt（S））。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10005;
int a[N];
int main()
{
    int m, c = 0;
    cin>>m;
    for(int i=1; i*(i-1)<2*m; i++)
    {
        if((2*m-i*(i-1))%(2*i)==0)
            a[c++] = (2*m-i*(i-1))/(2*i);
    }
    sort(a, a+c);
    for(int i=0; i<c-1; i++)
        printf("%d
", a[i]);
    if(c==1) puts("No Solution");
    return 0;
}