数学建模法-Dijkstra算法

Posted 2020-12-04 qling

一、引言

         哈喽大家好，今天要讲的是图论中的一个经典的算法。是一种叫Dijkstra算法的东东。这个算法是干什么用的呢。首先大家先看下面这幅图：        

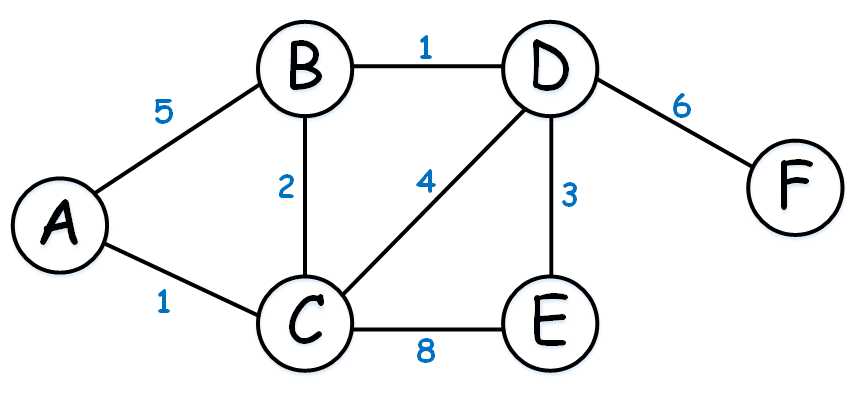
        这个东西是什么呢。我们可以这样理解，假如A到F表示6个地点。那些连接线就是道路。连接线上的数字就是两个地点间的距离。这样讲是不是很直观呢。好了，假如博主家在A点，博主的女神家在F点，有一天博主想去女神家，就有很多条路线可以走。可是博主很懒诶，肯定就想走最短的路线。那么，怎么才能很快的就求解出最短的路线呢。Dijkstra算法就是用来解决这样的问题的。

二、Dijkstra算法的思想

        Dijkstra算法的思想其实很直观，就是我从A点出发，发现可以走的路就只有C和B了，那么我肯定就要走最近的那条路，也就是C（同时记录C与A的距离）。接下来，我们从C点出发，可以走的路有B和D和E，再选择出最近的一条路，也就是B点（同时也记录C与B的距离）。通过每次不断的走最短的路线。最后走到F的路线也肯定是最短的。这就是Dijkstra算法的思想。当然讲起来很简单，计算起来有时候也会遇到一些其他因素。接下来我会尽可能通俗易懂的讲这个算法的过程讲清楚。

三、Dijkstra算法步骤

        接下来的讲解， 可能有点生涩，我会先写出来再慢慢解释。

        首先，我们要先确定我们的起点。在这里我们定我们的起点为A。但这样还不够，我们要写成（端点，端点与起点之间的距离）的形式。因此，我们的A就要写为(A, 0)。

        准备工作做完了，我们开始吧。

        (1) 首先从(A, 0)开始，A端点所连接的两个点分别是(B, 5)和(C, 1)。我们先把(B, 5)和(C, 1)存到Box里，并且根据大小来排序（最小排左边）。如下图

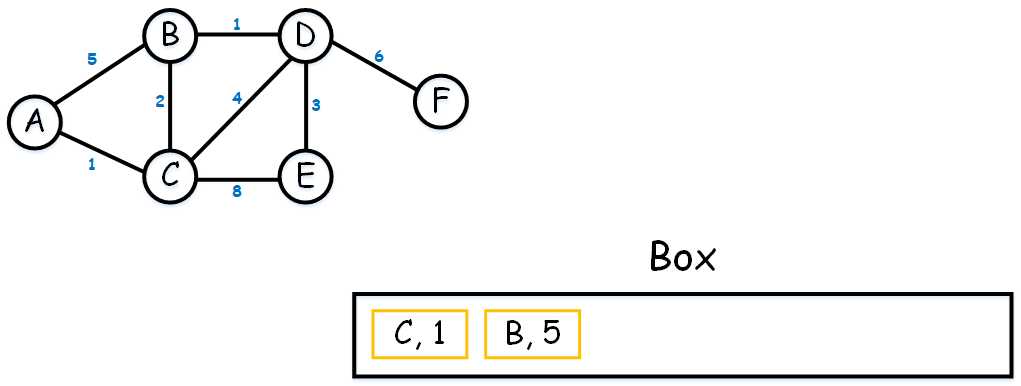
         显然，(C, 1)是最小的，因此，A点到下一个点的最短路线点是(C, 1)。我们不妨再创建一个Box吧，称之为Box3吧。称Box3是因为有3行。第一行表示图上所有的地点，第二行表示对于第一行地点的前一个最短路线点，第三行表示第一行的地点与原点的距离。如下：

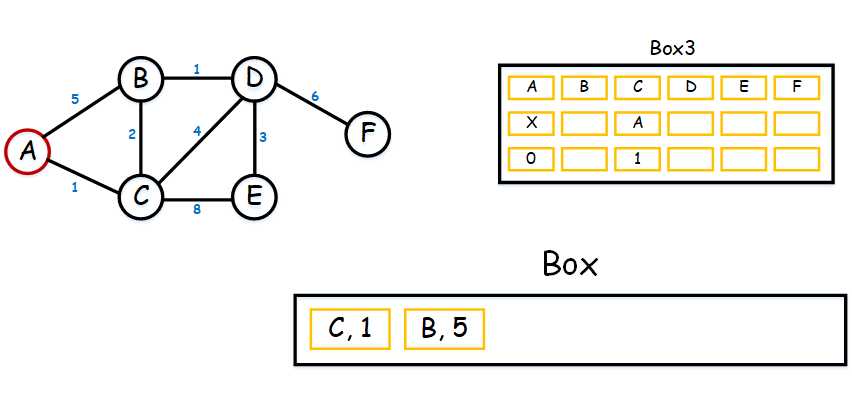
        大家可以看到， 第二行第一列，因为我们的A就是起点，在A之前并没有什么点，因此打×，下面的0表示无的意思。因为我们现在求出我们的(C, 1)是我们的下一个最短路线点，并且C是从A走过去的，故第二行第三列是A ，其下面的1表示从起点到C的最短距离为1。

        (2) 好了，现在，既然确定了(A, 0)的下一个点是(C, 1)。接下来，我们要从(C, 1)出发，我们看看，跟(C, 1)连接的点有(B, 3)点(注意，是3不是2，我们说过是与起点的距离，即A-C-B)和(D, 5)点以及(E, 9)。把其填入Box里面并排序。如下：

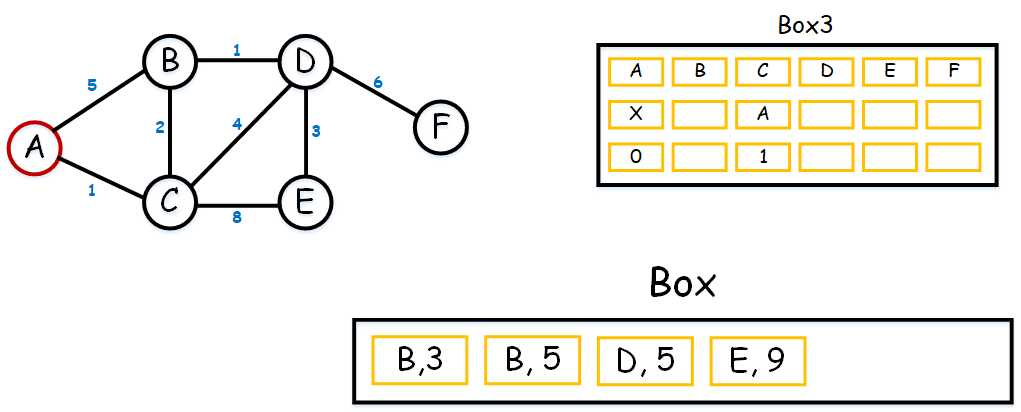
         咦，这时候你可能会有疑问，为什么(C, 1)不见了，而且有两个B，一个是(B, 3)一个是(B, 5)。别急，我正要讲。当我们确定好最短距离的点后，我们就将其从Box里面剔除掉，因为C已经被用过了。而至于为何有两个B。大家还记得，当我们直接从A到B的时候，距离是5；而当我们从A到C到B的时候，距离是3。因此就有两个了。现在，在这个Box里面我们找到最小的数，就是(B, 3)。这样我们就可以在Box3也填入我们的数，如下：

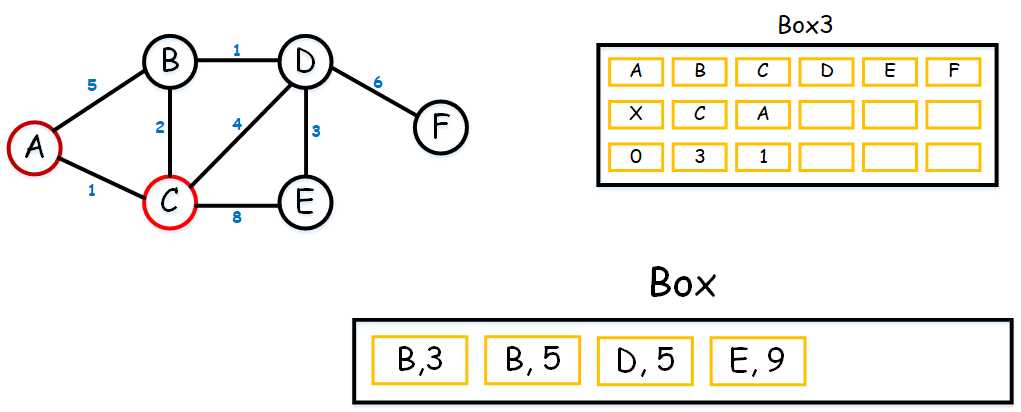
         (3) 好的，让我们继续，接下来我们从(B, 3)开始，由于B的连接点只剩(D, 4)(已经用过的点不能再用，故A和C不算。毕竟我们肯定不走回头路呀hhh)。填入Box并排序，可以得到(D, 4)是最小的数，填入Box3中。如下

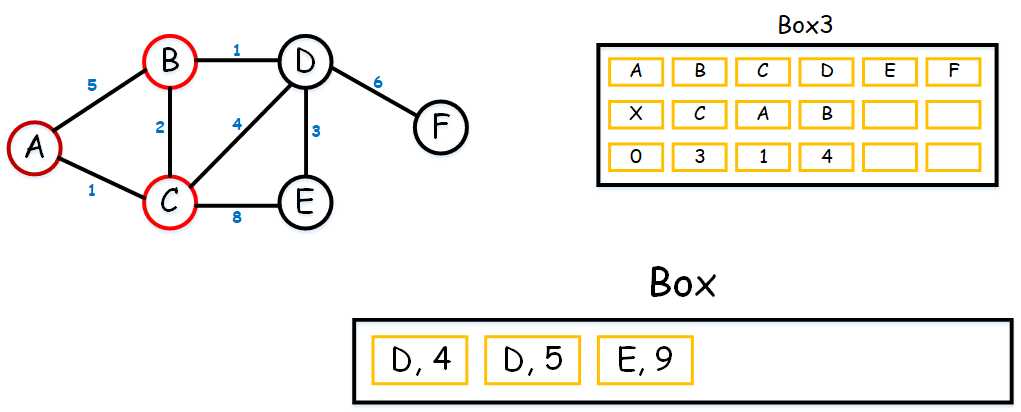         (4) 好了，接下来我们从(D, 4)出发，跟(D, 4)连接的有(E, 7)和(F, 10)，填入Box并排序，可以得到(E, 7)是最小的数，填入Box3中。如下：

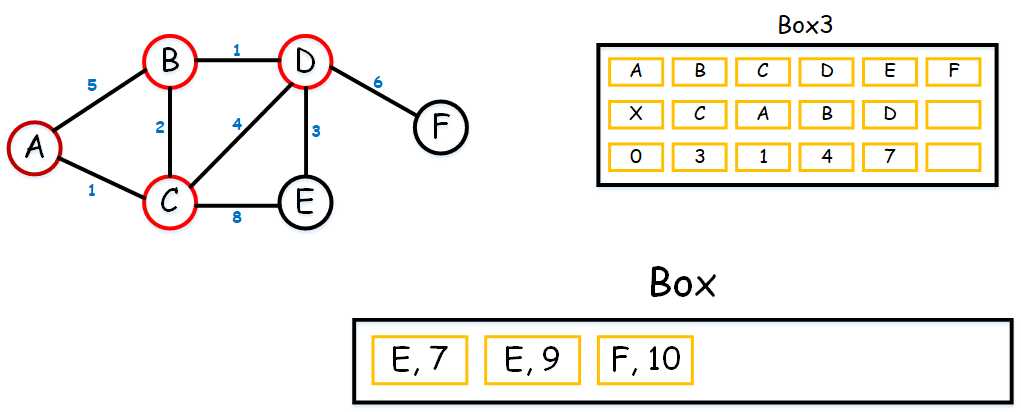
        (5) 好，接下来我们从(E, 7)出发，诶这时候发现，E已经没有可连接的点了。那Box里面只剩(F, 10)了。把Box3最后一列填完。那我们就找到了最短去博主女神家的路了。

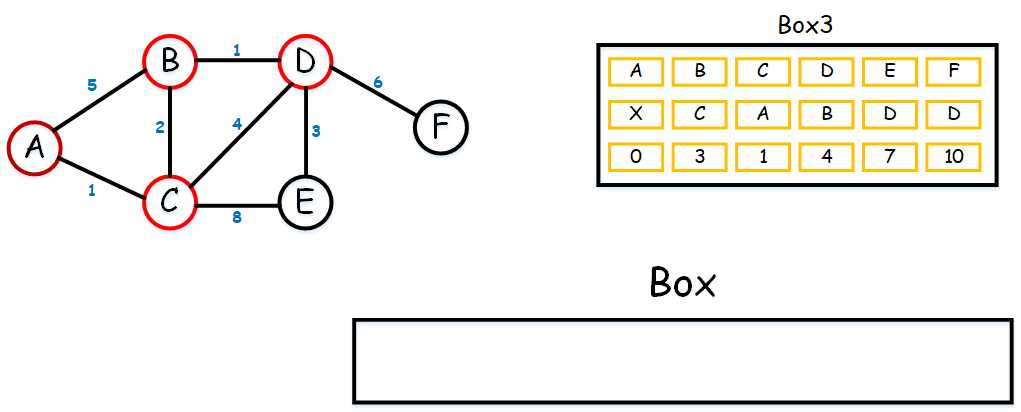
        现在，我们知道从A到F的最短路线和距离分别是A-C-B-D-F和10。现在我们要谈谈Box3，当我们完成这个表后，我们不仅可以马上知道博主家到博主女神家的最短路线。还能知道任意点到起点的最短路线呢。比如说，我们想知从A到E的最短路线。看Box3，E的上一点是D，D的上一点是B，B的上一点是C，C的上一点是A。这样就得到A-C-B-D-E是最短路线。而Box3中E最下方的7就表示最短距离值哦。现在你们是不是搞懂了呢~^_^。

四、Dijkstra的Matlab实现

function [distance, path] = dijkstra(A, sn, en)
% [DISTANCE,PATH] = DIJKSTRA(A, SN, EN)
% returns the distance and path between the start node and the end node.
%
% A: adjcent matrix
% sn: start node
% en: end node

%% 初始化
%节点的数量n
n = length(A);
%以sn为起点的矩阵（distance vector）
D = A(sn,:);

vi = ones(1, n);    %让节点都可见
vi(sn) = 0;         %起点节点是不可见的 

%parent：即Box3中的第二行
parent = zeros(1, n);

%% 计算最短距离

for i = 1: n-1
    temp = zeros(1, n);
    count = 0;
    %把distance vector里面非顶点的距离值放进temp，以便后续比大小取出最短距离
    for j = 1: n
        if(vi(j))
            temp = [temp(1: count) D(j)];
        else
            temp = [temp(1: count) inf];
        end
        count = count + 1;
    end
    
    %找出最短距离的点，并设定为下次路径的顶点
    [~, index] = min(temp);
    vi(index) = 0;%让顶点不可见
    for k = 1: n
        if A(index, k) + D(index) < D(k)
            D(k) = A(index, k) + D(index);
            parent(k) = index;  %算出k的上一层最短路径点，即Index
        end
    end
end
%%迭代完成后，distance矩阵的数值都是相对应的最短距离
distance = D(en);

%%求出最短路径

path = [];
t = en; path(1) = t; count = 1;
while t ~= sn && t > 0
    p = parent(t);
    path = [p path(1:count)];    %从path里面 不断往左边放路径点,最右边是终点
    t = p;
    count = count + 1;
end
path(1) = sn;
path = path(1: count);

        验证一下，我们根据这篇的图例写出邻接矩阵（这里我当大家知道什么是邻接矩阵，不知道的自己百度一下哈）。得到如下：

A = [0 5 1 5 9 inf;
     5 0 2 1 inf inf;
　　　1 2 0 4 8 inf;
　　　inf 1 4 0 3 6;
　　　inf inf 8 3 0 inf;
　　　inf inf inf 6 inf 0];        

        然后，因为我们要算A到F的最短距离，因此sn = 1, en = 6。故在matlab中输入：

[distance, path]=dijkstra(A, 1, 6)

　　最后就得到如下结果：

distance =
    10
path =
     1     3     2     4     6

        1-3-2-4-6翻译过来也就是A-C-B-D-F。跟我们前面分析的一致。故正确。