[数据结构] 树森林的遍历

Posted 2023-02-05 MAKISE004

树的遍历

树的遍历方式有先根遍历和后根遍历。在下面树的遍历中，采用的都是孩子兄弟表示法构建的树。

树的先根遍历

树的先根遍历步骤

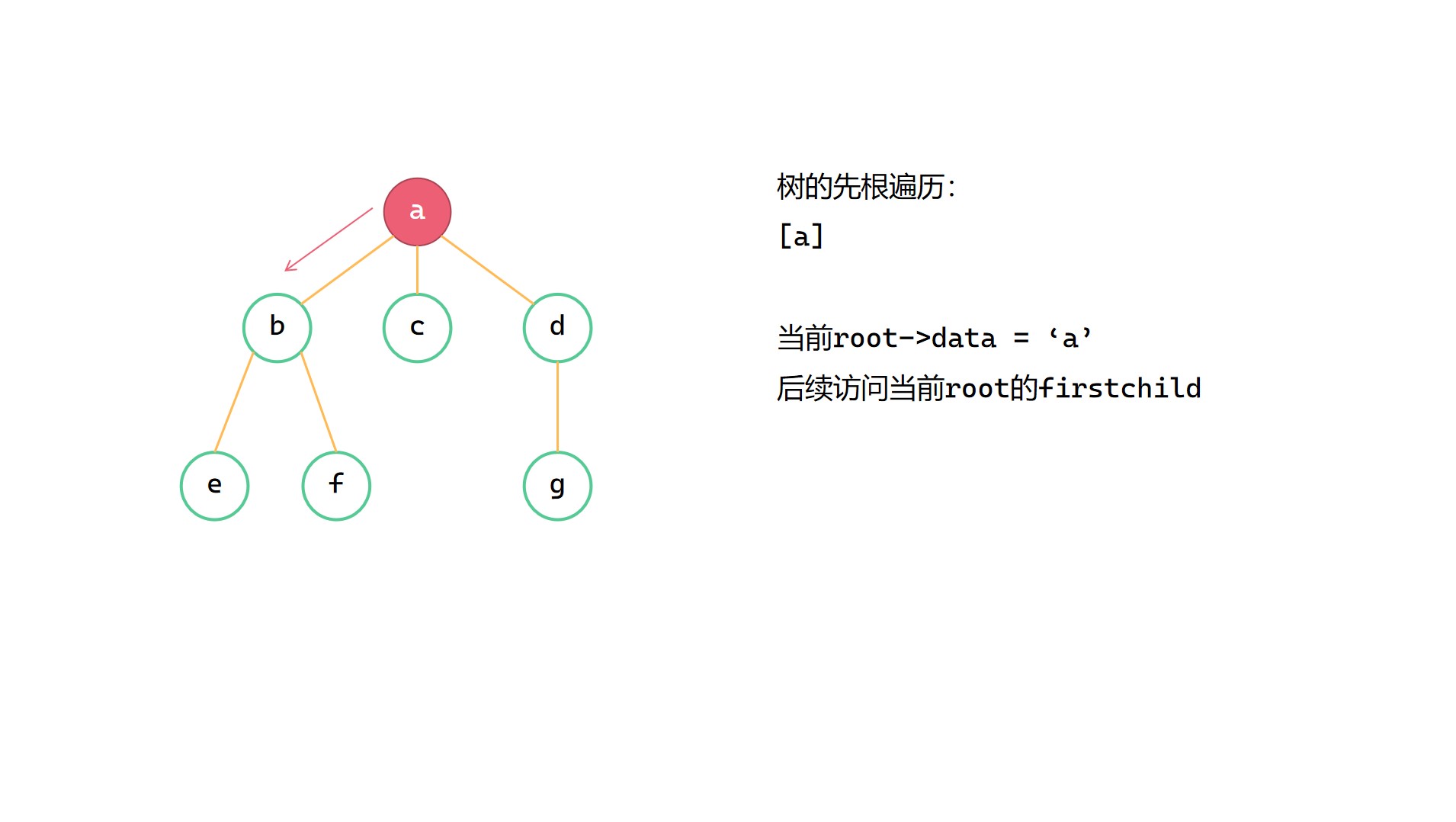
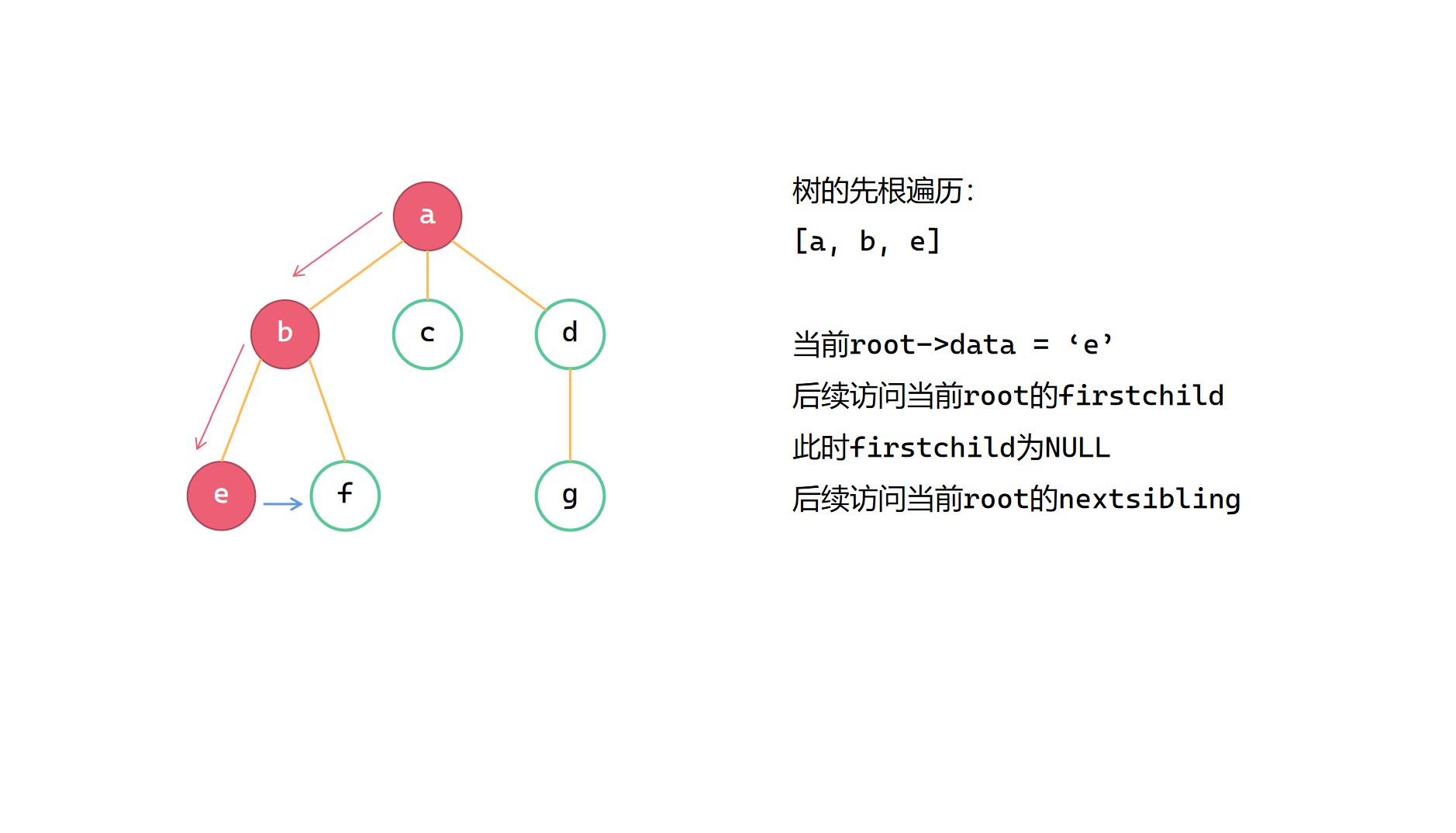
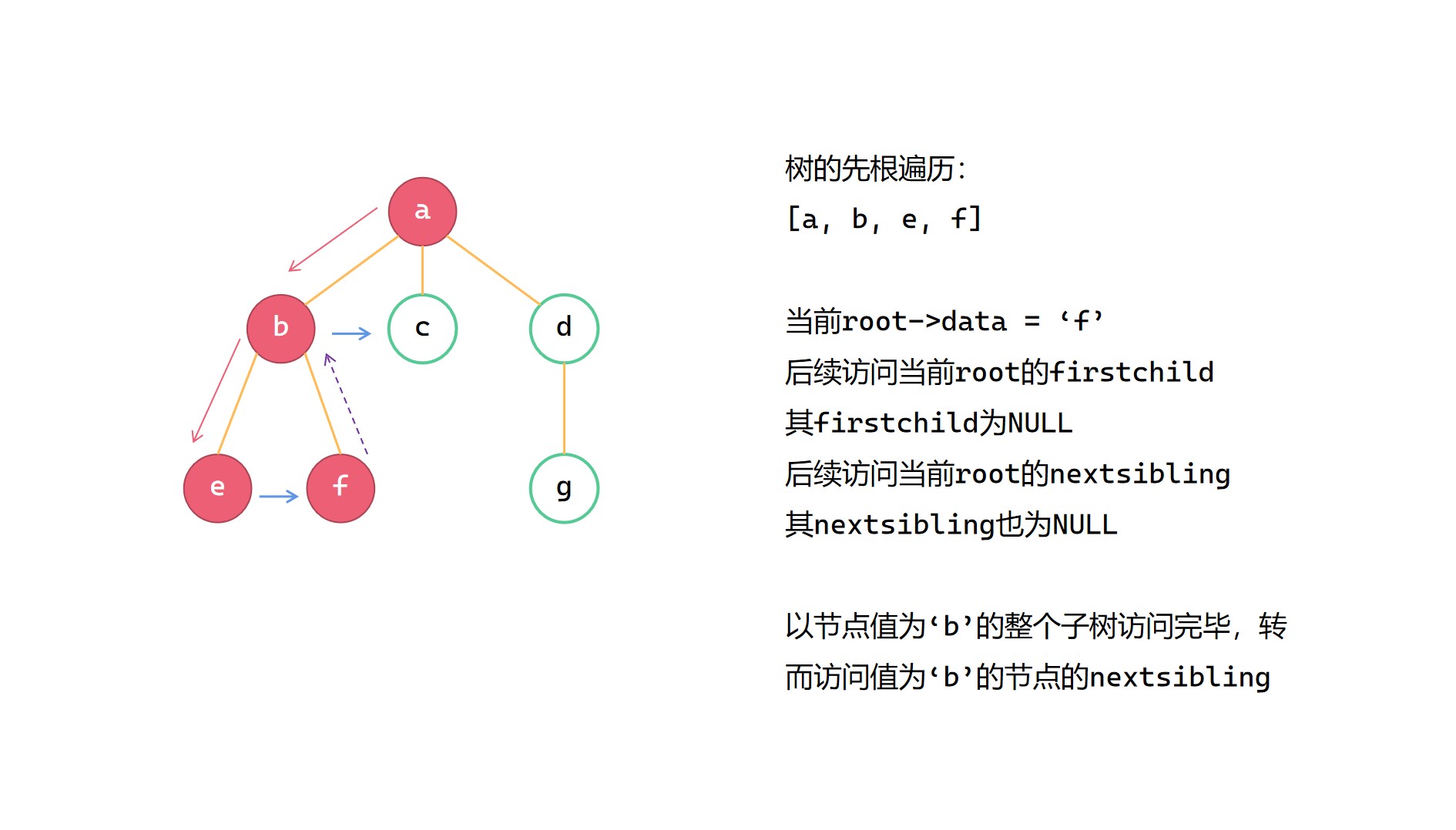
先根遍历就是先访问树的根节点，然后再依次访问树的孩子们。在这里我们需要用递归函数来实现树的先根遍历，先打印当前节点的数据，然后再递归访问其第一个孩子，再递归访问当前节点的兄弟。注意树的根节点是没有兄弟的，在第一层递归中实际只会递归访问其 firstchild，这一点在创建树的过程中也需注意。
递归函数停止递归的边界条件很简单，遇到空指针 NULL 停止即可。

假设函数名为 CStree_preorder ，则大致步骤如下：
（1）print(root->data)
（2）CStree_preorder(root->firstchild)
（3）CStree_preorder(root->nextsibling)

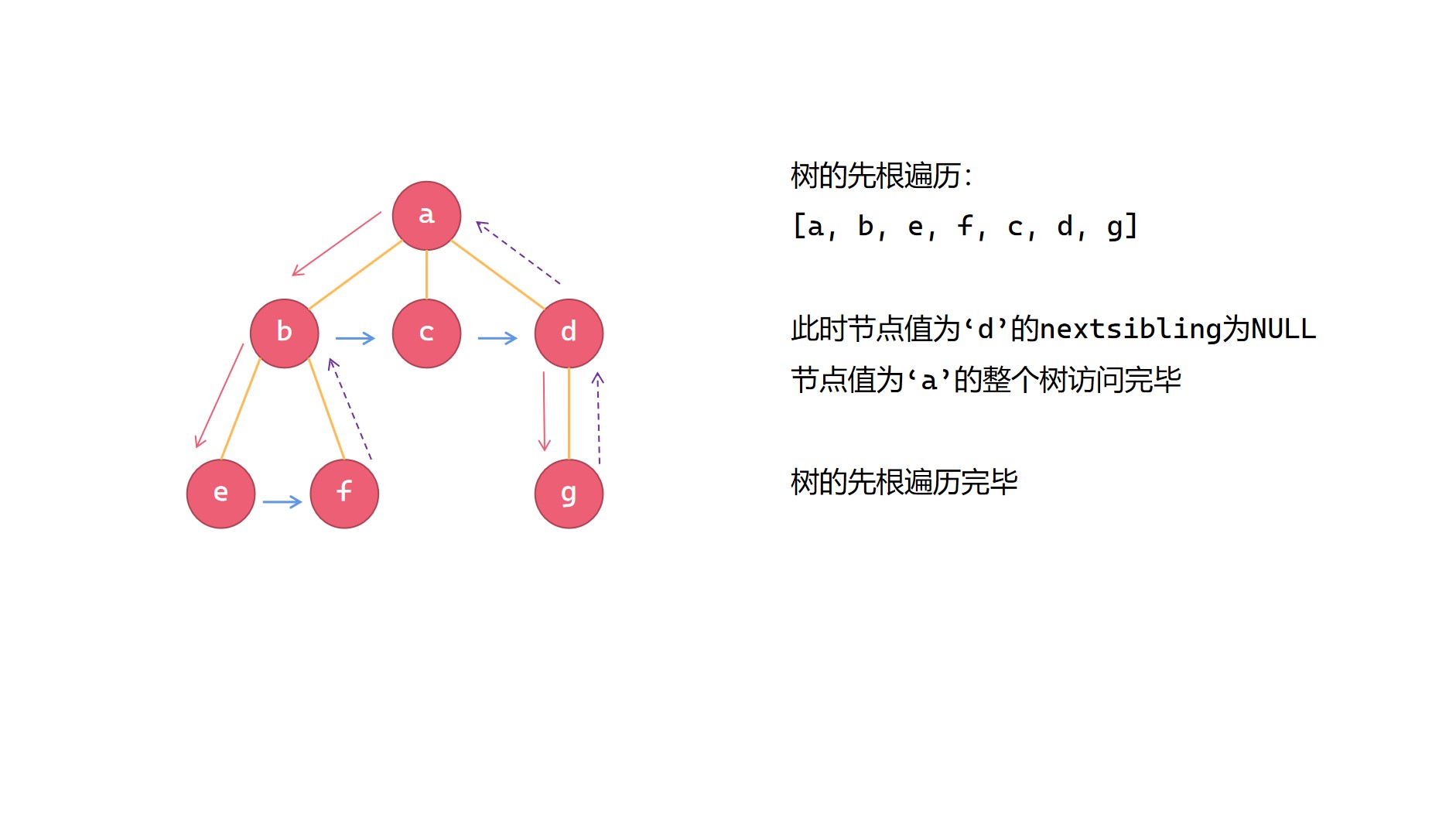
树的先根遍历图解

（1）

（2）

（3）

（4）

（5）

（6）

（7）

（8）

树的先根遍历小技巧

树的先根遍历可以看成是以根节点为起点，围绕整个树跑一圈，所经历的节点值的序列就是树的先根遍历的结果（重复出现过的节点值不再加入到序列中）。这一点和二叉树的前序遍历很像。

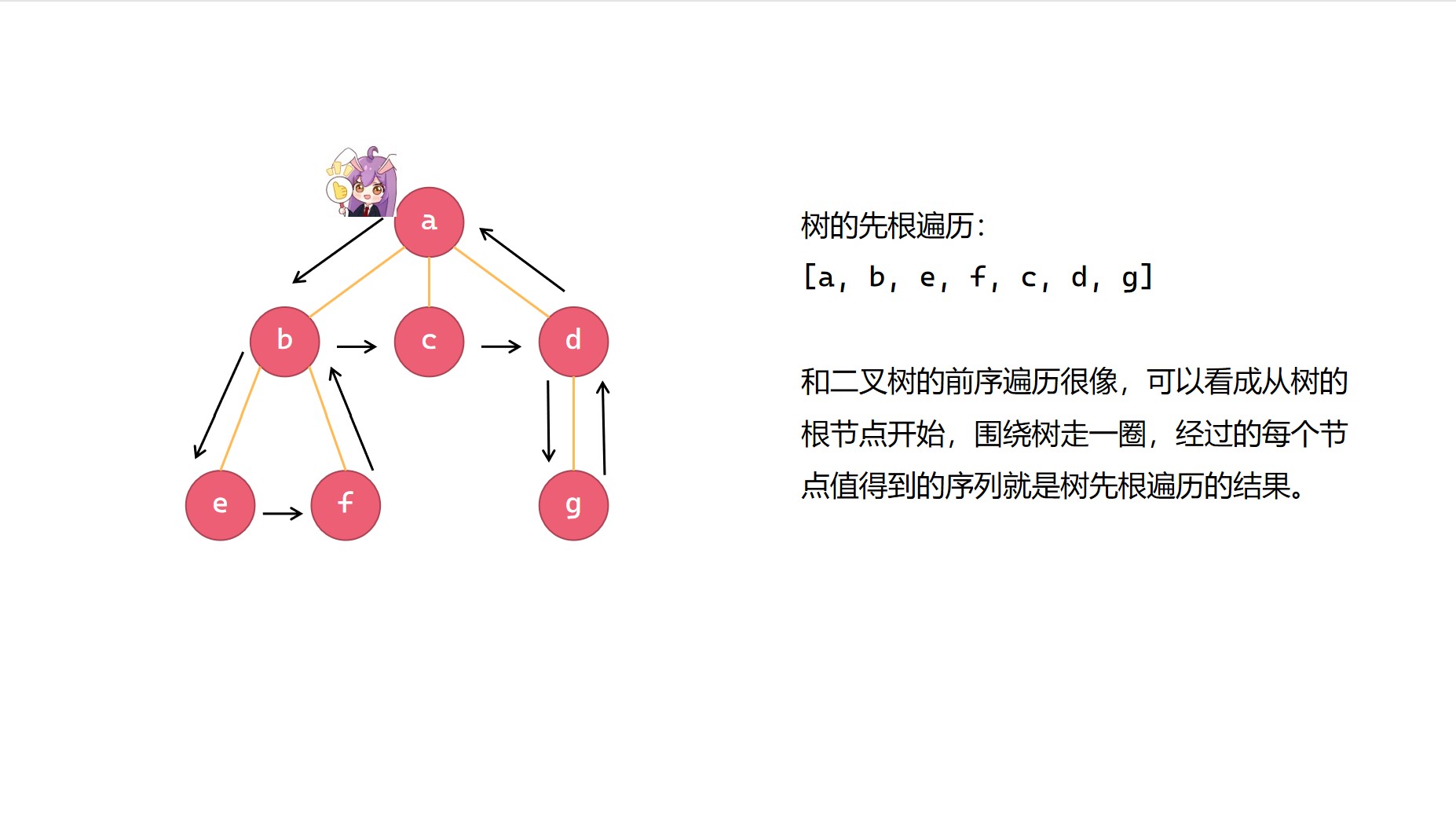
树的先根遍历代码

void CSTree_Show_Pre_Order(CSTree T)
    if(T == NULL)
        return;
    
    printf("%c ", T->data);
    CSTree_Show_Pre_Order(T->firstchild);	
    CSTree_Show_Pre_Order(T->nextsibling);

树的后根遍历

树的后根遍历步骤

后根遍历的顺序是先访问根节点的孩子们，然后访问根节点。我们还是用递归函数来解决，先递归访问当前节点的第一个孩子，然后打印当前节点的数据，最后再递归访问当前节点的兄弟。递归函数停止递归的边界条件很简单，遇到空指针 NULL 停止即可。

假设函数名为 CStree_postorder ，则大致步骤如下：
（1）CStree_postorder(root->firstchild)
（2）print(root->data)
（3）CStree_postorder(root->nextsibling)

树的后根遍历图解

（1）

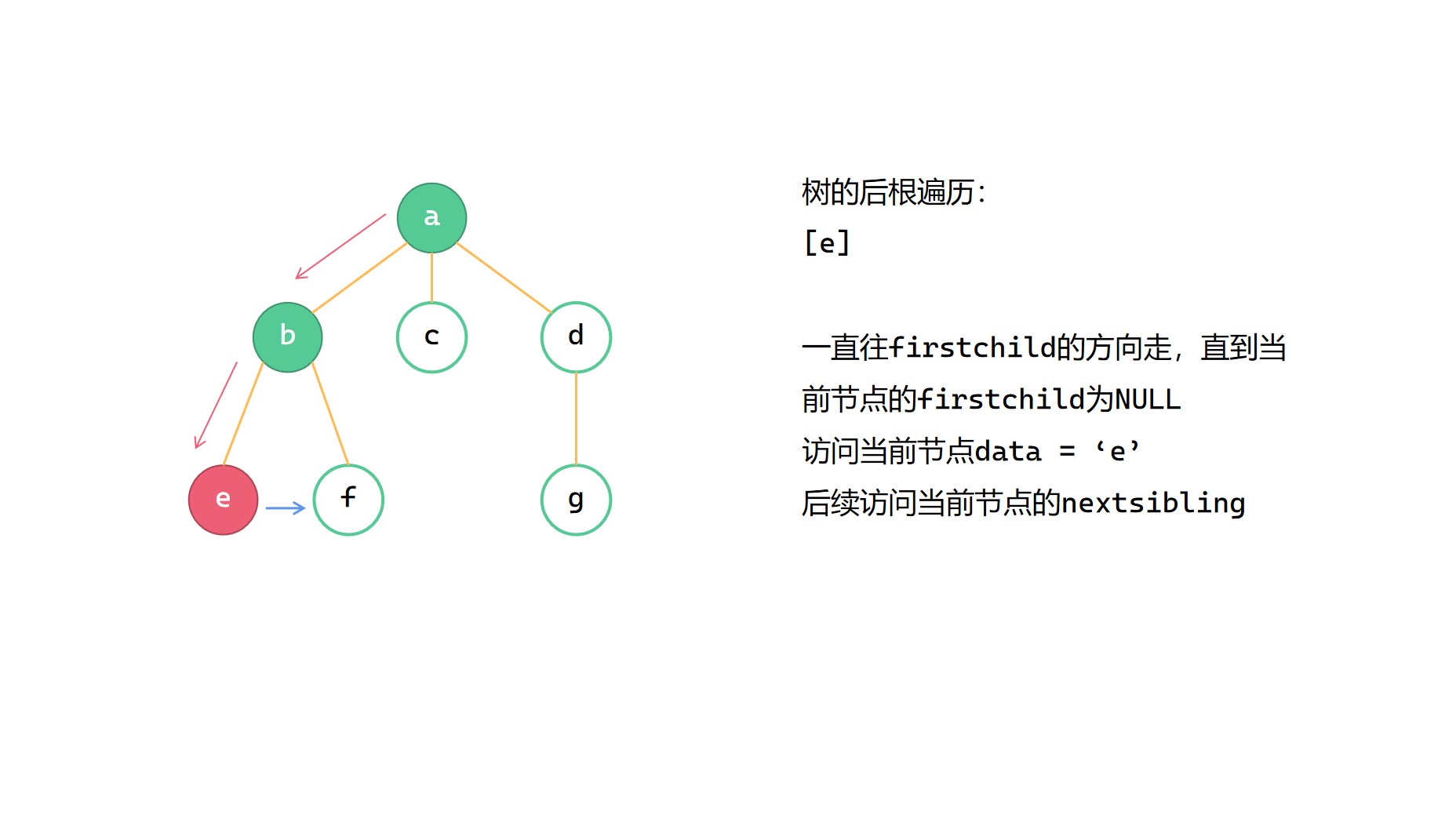
（2）

（3）

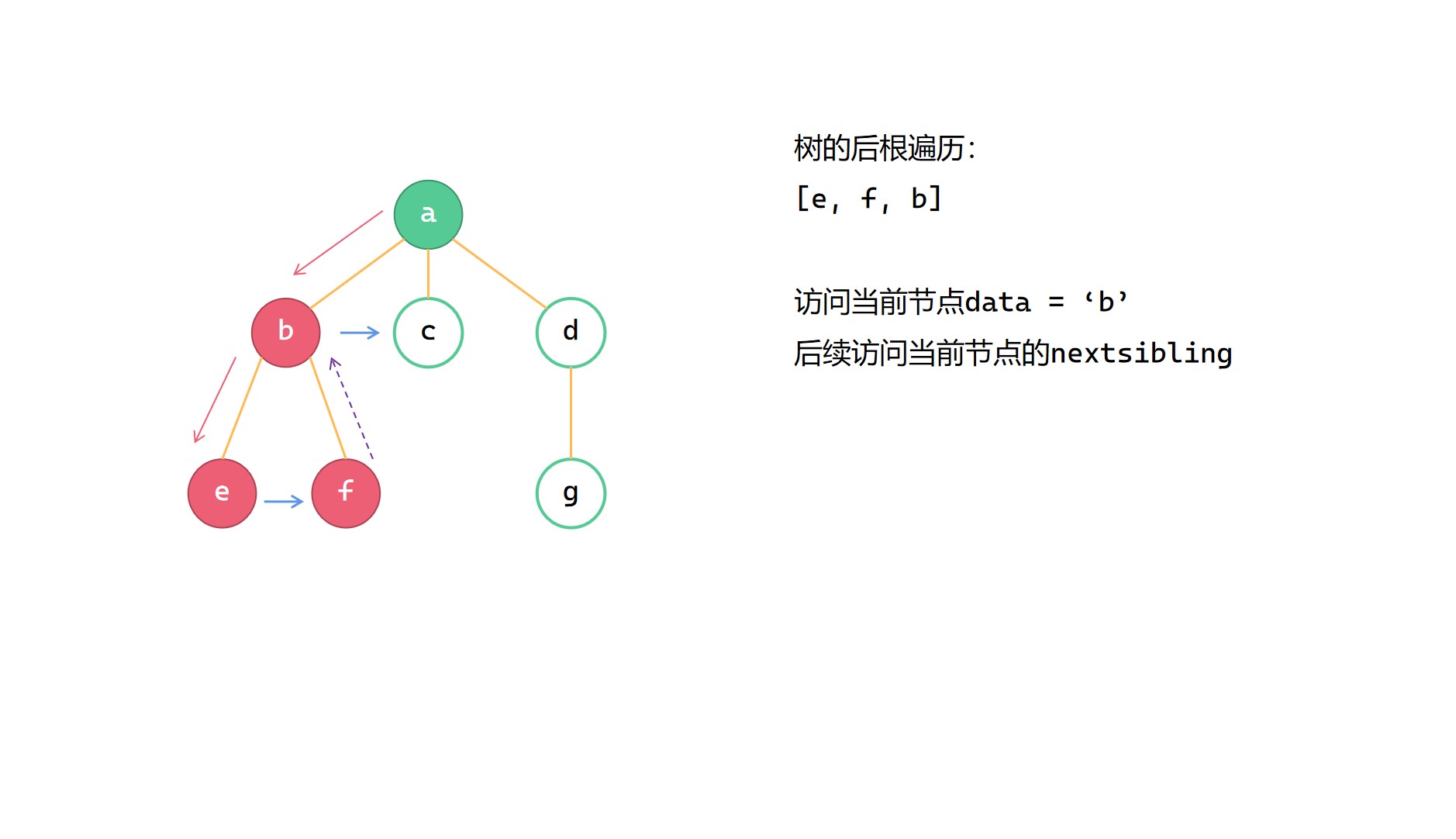
（4）

（5）

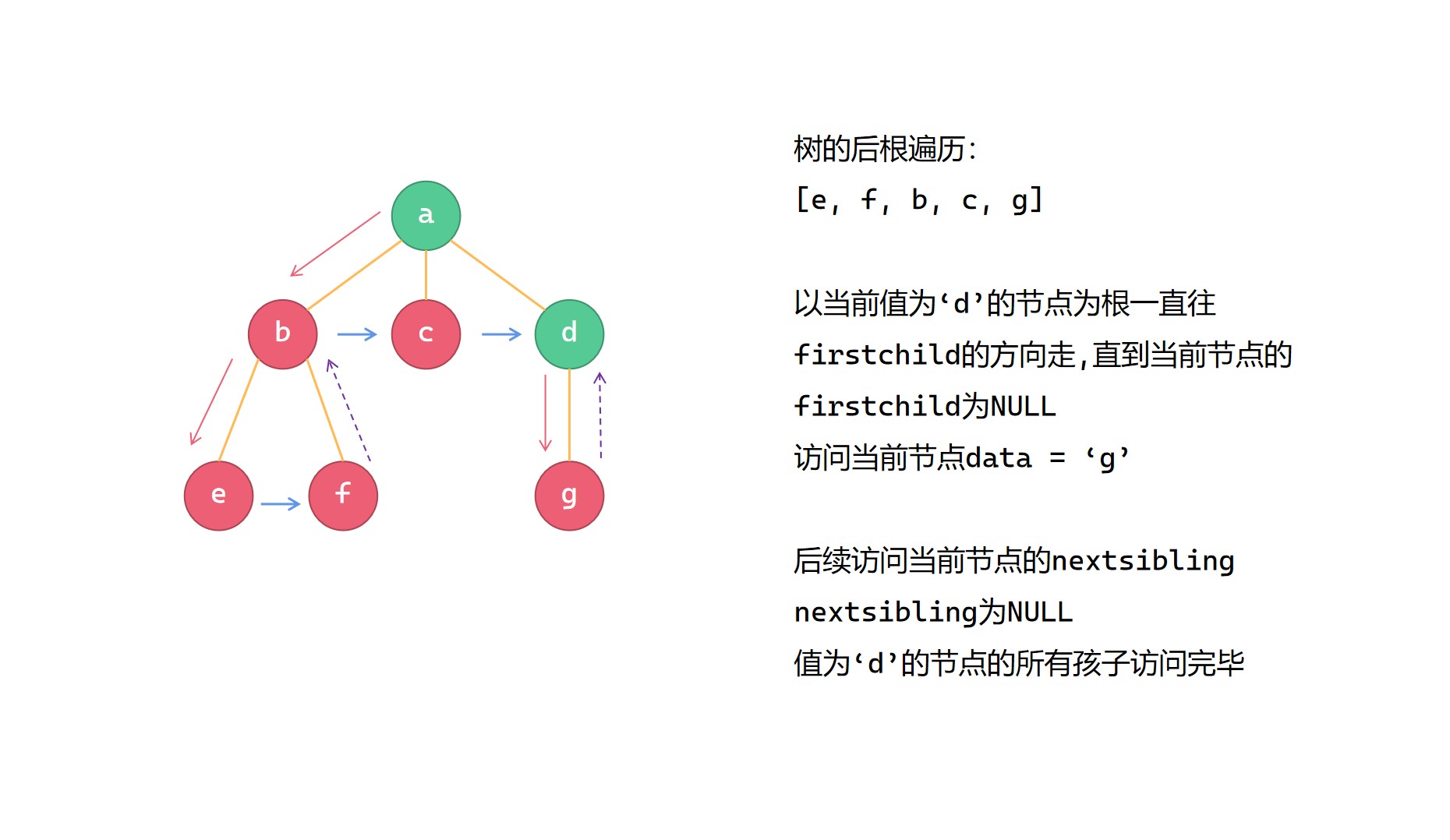
（6）

（7）

树的后根遍历小技巧

树的后根遍历可以看成是剪葡萄一样，将节点依次剪下后得到的序列就是树的后根遍历的结果，这一点和二叉树的后序遍历有点相似。

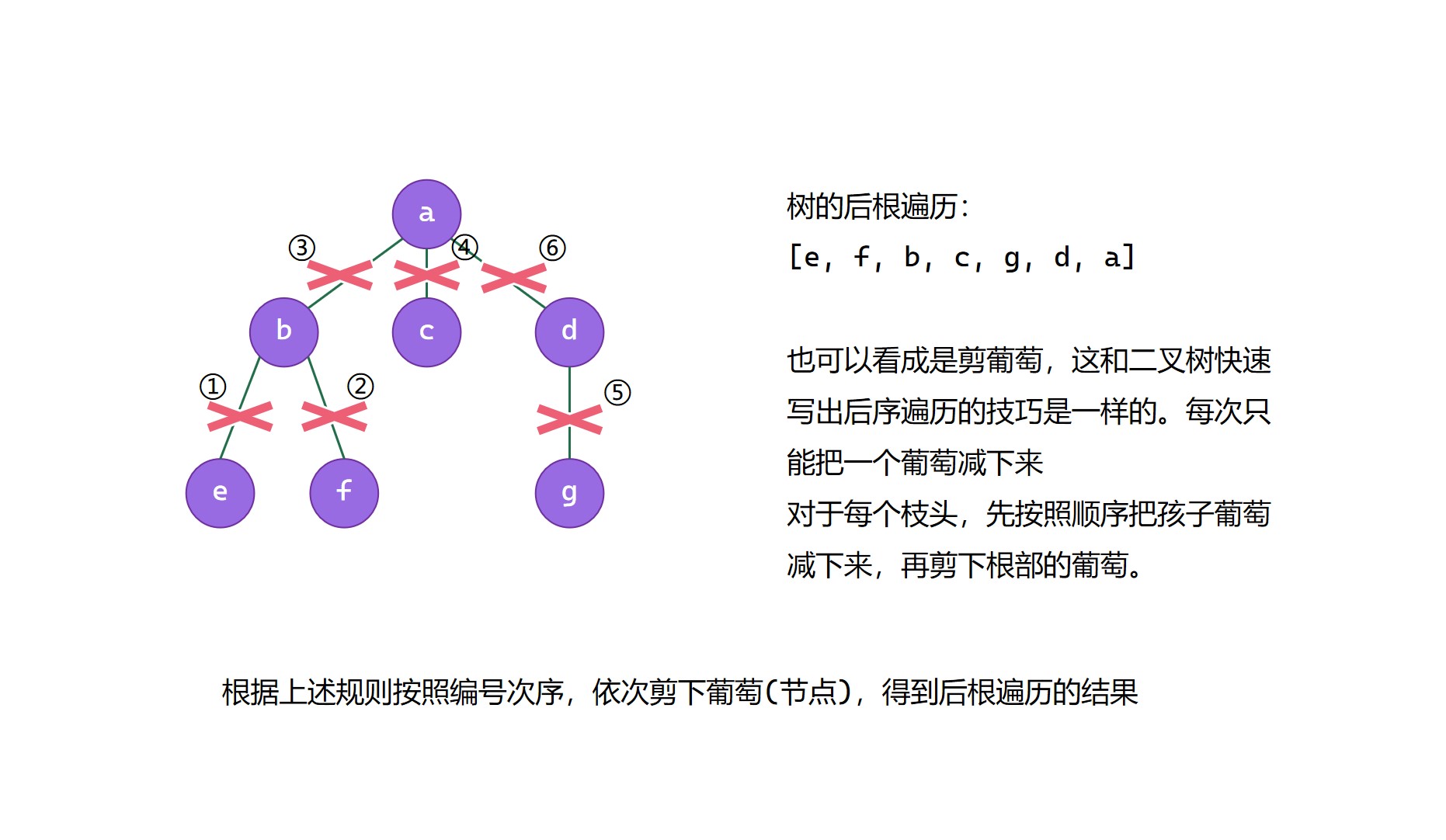
树的后根遍历代码

void CSTree_Show_Post_Order(CSTree T)
    if(T == NULL)
        return;

    CSTree_Show_Post_Order(T->firstchild);
    printf("%c ", T->data);
    CSTree_Show_Post_Order(T->nextsibling);

树的遍历与二叉树的遍历

树的先根遍历与二叉树的前序遍历

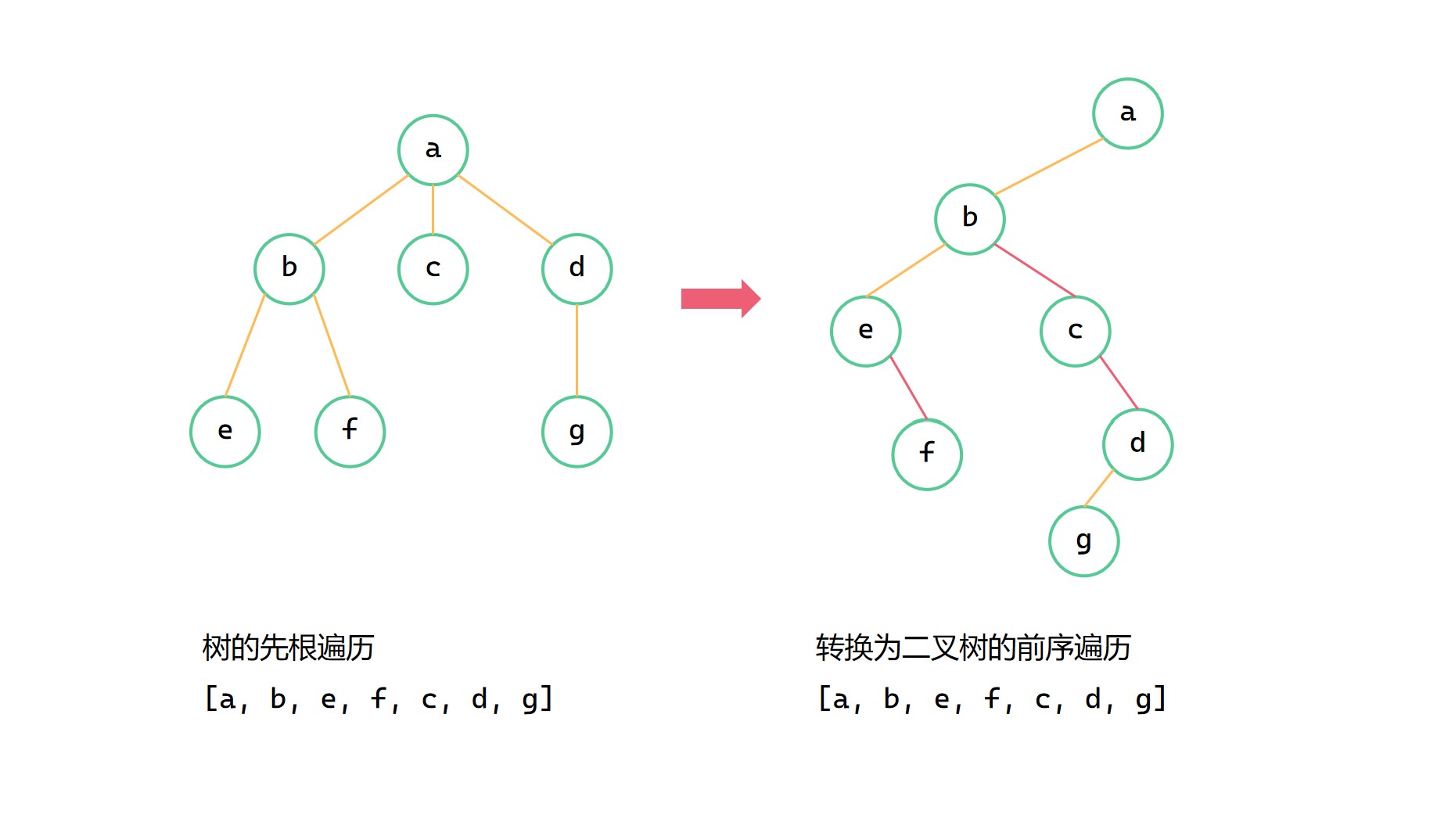
由于我们使用的是孩子兄弟表示法构建的树，实际上我们将树以二叉链式的结构存储了起来，其本质上已经转换为一棵二叉树。树的 firstchild 对应了二叉树的 leftchild，树的 nextsibling 对应了二叉树的 rightchild 。

结合上文先根遍历的代码和其对应关系，我们可以发现其递归操作的顺序和二叉树的前序遍历是一样的。所以我们其实可以先将树转换为二叉树，然后进行前序遍历，得到的遍历结果和树的先根遍历是一样的。

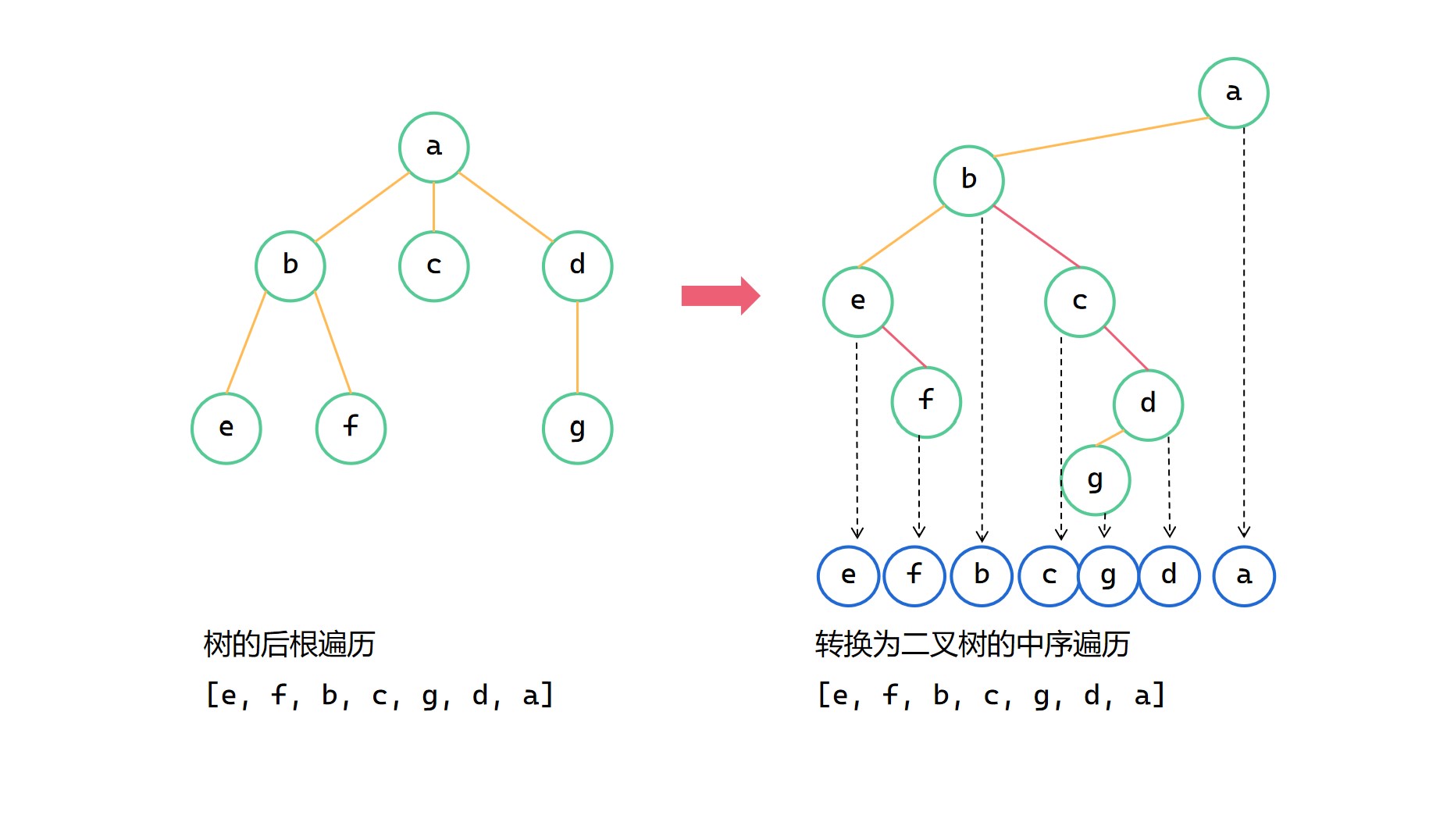
树的后根遍历与二叉树的中序遍历

同理，结合上文后根遍历的代码和其对应关系，我们可以发现其递归操作的顺序和二叉树的中序遍历是一样的。所以我们其实可以先将树转换为二叉树，然后进行中序遍历，得到的遍历结果和树的后根遍历一样。

---

森林的遍历

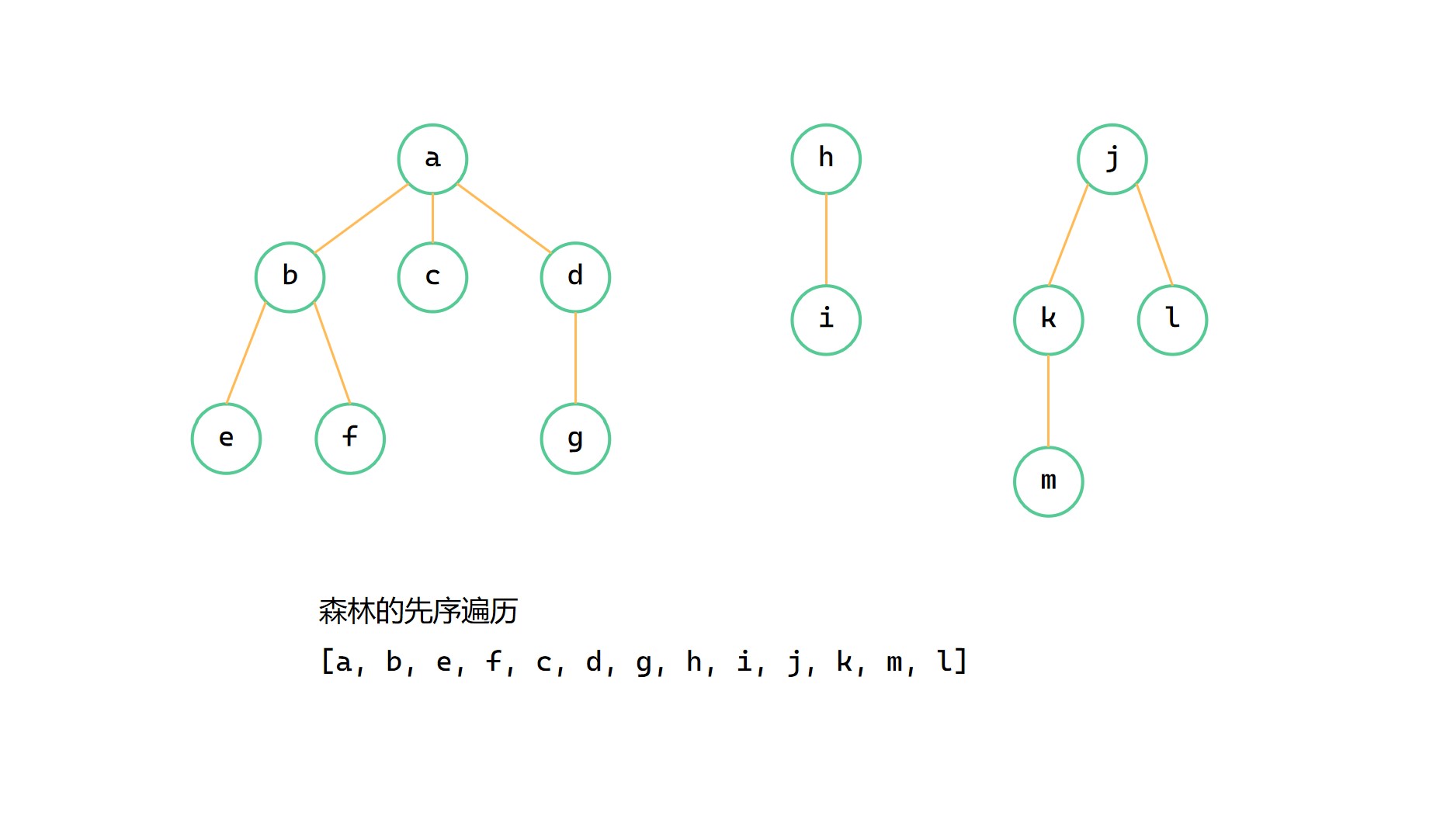
森林的先序遍历

森林的先序遍历步骤

森林的先序遍历顺序即按照森林的每棵树的顺序，对每一棵树进行先根遍历。

森林的先序遍历代码

//森林的先序遍历
void Forest_Show_Pre_Order(Forest F)
    for(int i = 0; i < F->n; i++)
        CSTree_Show_Pre_Order(F->ct[i]);

森林的中序遍历

森林的中序遍历步骤

森林的先序遍历顺序即按照森林的每棵树的顺序，对每一棵树进行后根遍历。

森林的中序遍历代码

//森林的中序遍历
void Forest_Show_Post_Order(Forest F)
    for(int i = 0; i < F->n; i++)
        CSTree_Show_Post_Order(F->ct[i]);

森林的遍历与二叉树的遍历

森林的先序遍历与二叉树的前序遍历

森林在转换为二叉树的过程中，将每个树根节点用 rightchild 进行了连接。转换成二叉树递归遍历完根节点的左子树时，接下来递归遍历其右子树，而此右子树也是森林中第二个树的根节点，以此类推，可以得出转换成二叉树的前序遍历正好就是森林先序遍历的结果。

森林的先序遍历

转换为二叉树的前序遍历

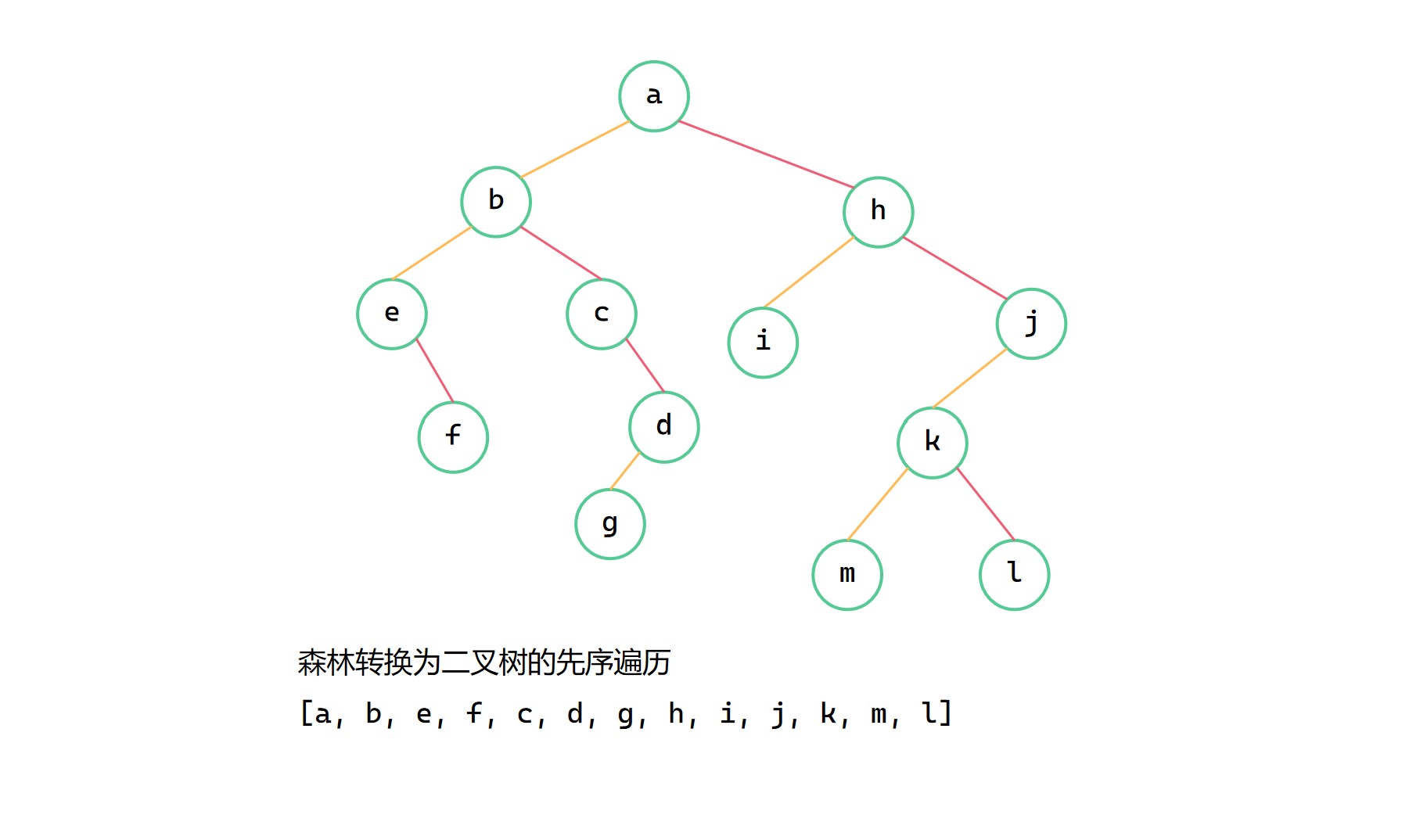
森林的中序遍历与二叉树的中序遍历

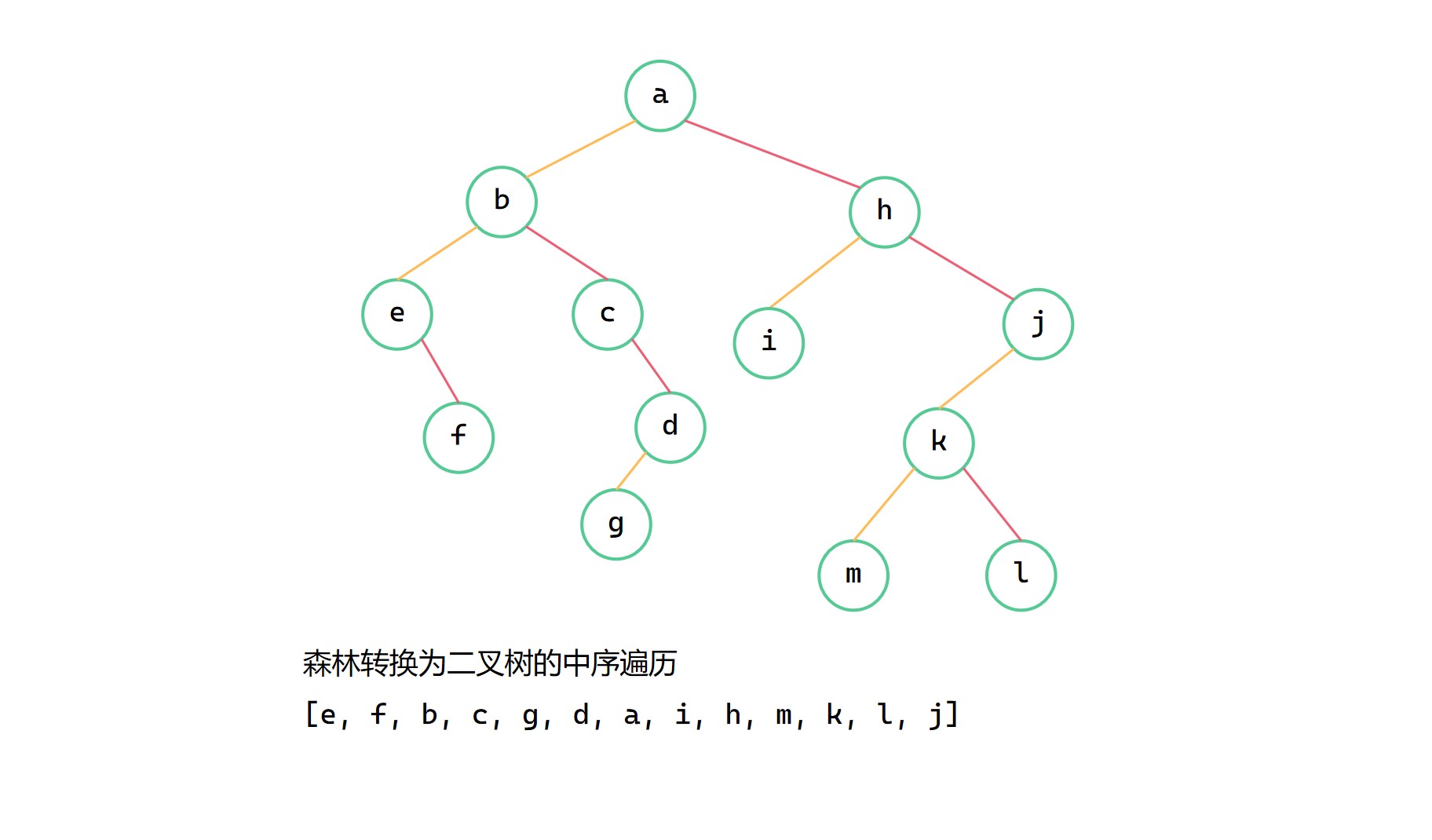
同理，森林转换为二叉树的中序遍历，正好对应了森林中序遍历的结果。

森林的中序遍历

转换为二叉树的中序遍历

---

程序测试

程序代码

#include<stdio.h>
#include<stdlib.h>
#define MAX 100

typedef char Elemtype;
//树 (孩子兄弟表示法)
typedef struct CSNode

    Elemtype data;
    struct CSNode *firstchild;      //第一个孩子
    struct CSNode *nextsibling;     //下一个兄弟

CSNode, *CSTree;


//二叉树 结构体
typedef struct BiNode

    Elemtype data;
    struct BiNode *leftchild;       //左儿子
    struct BiNode *rightchild;      //右儿子

BiNode, *BinaryTree;              


//森林 结构体
typedef struct 

    CSTree ct[MAX];
    int n;   //树的个数
	
forest, *Forest;



/*—————————————————————————————————————————————————————————————————————————————————————*/
//创建 树
CSTree Create_CSTree()
    Elemtype data;
    CSTree T;
    scanf("%c", &data);                       //输入节点数据
    getchar();

    if(data == \'#\')        //输入 - 以停止创建子树
        return NULL;
    T = (CSTree)malloc(sizeof(CSNode));
    T->data = data;

    printf("输入 %c 的第一个孩子数据(#停止): ", data);  //递归创建
    T->firstchild = Create_CSTree();
    printf("输入 %c 的下一个兄弟数据(#停止): ", data);  
    T->nextsibling = Create_CSTree();
 
    return T;




/*—————————————————————————————————————————————————————————————————————————————————————*/
//树 转化为 二叉树
BinaryTree CSTree_Transform_to_BinaryTree(CSTree ct)
    if(!ct) return NULL;

    BinaryTree T = (BinaryTree)malloc(sizeof(BiNode));
    T->data = ct->data;
    //相当于将left变为firstchild, 将right变为nextsibling 本质的形态没有改变
    T->leftchild = CSTree_Transform_to_BinaryTree(ct->firstchild);
    T->rightchild = CSTree_Transform_to_BinaryTree(ct->nextsibling);

    return T;



//二叉树 转化 为树
CSTree BinaryTree_Transform_to_CSTree(BinaryTree bt)
    if(!bt)	return NULL;

    CSTree T = (CSTree)malloc(sizeof(CSNode));
    T->data = bt->data;
    //相当于将firstchild变为left, 将nextsibling变为right 本质的形态没有改变
    T->firstchild = BinaryTree_Transform_to_CSTree(bt->leftchild);
    T->nextsibling = BinaryTree_Transform_to_CSTree(bt->rightchild);

    return T;



//森林 转化为 二叉树
BinaryTree Forest_Transform_to_BinaryTree(CSTree ct[], int low, int high)
    if(low > high)	return NULL;

    //每个树变成二叉树
    BinaryTree T = CSTree_Transform_to_BinaryTree(ct[low]);  
    //通过rightchild连接每一个二叉树的根节点
    T->rightchild = Forest_Transform_to_BinaryTree(ct, low + 1, high);

    return T;



//二叉树 转化为 森林
Forest BinaryTree_Transform_to_Forest(BinaryTree bt)
    Forest F = (Forest)malloc(sizeof(forest));
    BinaryTree p = bt;	
    BinaryTree q = NULL;

    int count = 0;
    while(p)
	q = p->rightchild;    //q指向要切断连接的下一个节点(即其右儿子)
	p->rightchild = NULL; //切断连接 形成单独的树

	F->ct[count++] = BinaryTree_Transform_to_CSTree(p);//二叉树 转化为 树存到森林中
	p = q;    //p指向下一个节点 重复操作
    

    F->n = count; //记录森林中 树的个数
    return F;




/*—————————————————————————————————————————————————————————————————————————————————————*/
//前序 递归遍历二叉树
void BinaryTree_Show_Pre_Order(BinaryTree T)
    if(T == NULL)
	return;

    printf("%c ", T->data);	
    BinaryTree_Show_Pre_Order(T->leftchild);
    BinaryTree_Show_Pre_Order(T->rightchild);



//中序 递归遍历二叉树
void BinaryTree_Show_Infix_Order(BinaryTree T)
    if(T == NULL)
        return;

    BinaryTree_Show_Infix_Order(T->leftchild);
    printf("%c ", T->data);
    BinaryTree_Show_Infix_Order(T->rightchild);



//后序 递归遍历二叉树
void BinaryTree_Show_Post_Order(BinaryTree T)
    if(T == NULL)
	return;

    BinaryTree_Show_Post_Order(T->leftchild);
    BinaryTree_Show_Post_Order(T->rightchild);
    printf("%c ", T->data);




/*—————————————————————————————————————————————————————————————————————————————————————*/
//树的先根遍历  (相当于将firstchild当做left, 将nextsibling当做right)
void CSTree_Show_Pre_Order(CSTree T)
    if(T == NULL)
	return;
    
    printf("%c ", T->data);
    CSTree_Show_Pre_Order(T->firstchild);	
    CSTree_Show_Pre_Order(T->nextsibling);



//树的后根遍历 写法和二叉树的中序遍历一样(相当于将firstchild当做left, 将nextsibling当做right)
void CSTree_Show_Post_Order(CSTree T)
    if(T == NULL)
	return;

    CSTree_Show_Post_Order(T->firstchild);
    printf("%c ", T->data);
    CSTree_Show_Post_Order(T->nextsibling);




/*—————————————————————————————————————————————————————————————————————————————————————*/
//森林的先序遍历
void Forest_Show_Pre_Order(Forest F)
    for(int i = 0; i < F->n; i++)
	CSTree_Show_Pre_Order(F->ct[i]);



//森林的中序遍历
void Forest_Show_Post_Order(Forest F)
    for(int i = 0; i < F->n; i++)
	CSTree_Show_Post_Order(F->ct[i]);




/*—————————————————————————————————————————————————————————————————————————————————————*/
int main()
    CSTree F[3];
    for(int i = 0; i < 3; i++)
        printf("创建第 %d 棵树 输入根节点(注意根节点无兄弟):\\n", i + 1);
        F[i] = Create_CSTree();
        printf("\\n");
    

    printf("第一棵普通树后根遍历: \\n");
    CSTree_Show_Post_Order(F[0]);
    printf("\\n");

    printf("第二棵普通树先根遍历: \\n");
    CSTree_Show_Pre_Order(F[1]);
    printf("\\n");

    printf("三棵树组成的森林转化为二叉树之后中序遍历: \\n");
    //如果是一个Forset结构体指针F  Foresr_Transform_to_BinaryTree(F->ct, 0, (F->n) - 1)
    BinaryTree bt = Forest_Transform_to_BinaryTree(F, 0, 2);
    BinaryTree_Show_Infix_Order(bt);
    printf("\\n");

    printf("二叉树再次转换为森林之后先根遍历: \\n");
    Forest backF = BinaryTree_Transform_to_Forest(bt);
    Forest_Show_Pre_Order(backF);
    printf("\\n");

程序运行结果

一切都是命运石之门的选择，本文章来源于博客园，作者：Amαdeus，出处：https://www.cnblogs.com/MAKISE004/p/17091971.html，未经允许严禁转载