树的存储结构以及树和森林的遍历(C语言)
Posted bfhonor
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树的存储结构以及树和森林的遍历(C语言)相关的知识,希望对你有一定的参考价值。
一、树的存储结构
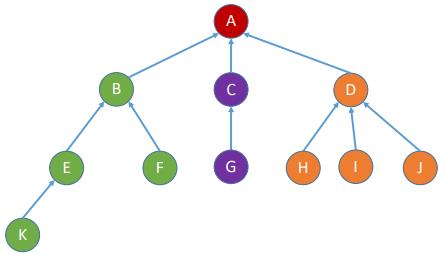
(一)双亲表示法(顺序存储)
- 双亲表示法:每个结点中保存指向双亲的“指针”

#define MAX_TREE_SIZE 100 //树中最多结点数
typedef struct{ //树的结点定义
ElemType data; //数据元素
int parent; //双亲位置域
}PTNode;
typedef struct{
PTNode nodes[MAX_TREE_SIZE];//树的类型定义
int n; //双亲表示
}PTree;
1. 添加元素
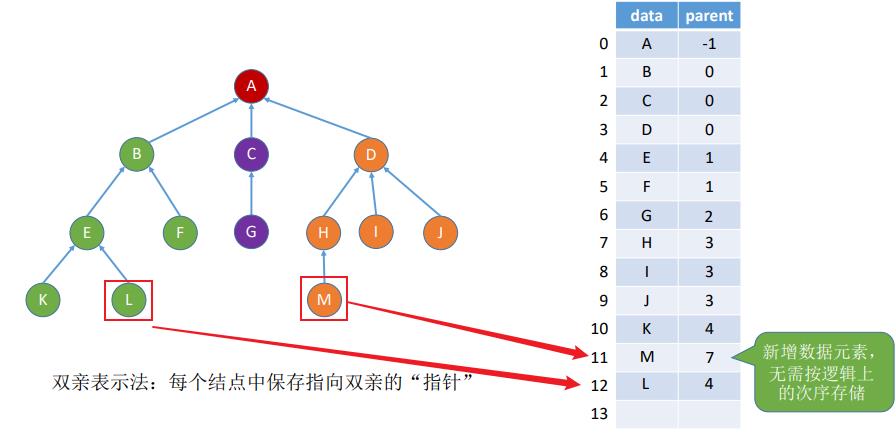
2. 删除元素
- 方案一:只需要parent双亲位置域设置成-1即可。

- 方案二:将最下的面的元素替换掉要删除的元素即可。

- ❗❗❗如果删除的不是叶子结点呢?❗❗❗那么就需要将其删除结点的孩子节点也删除掉。
3. 优缺点
- 优点:查指定结点的双亲很方便。
- 缺点:查指定结点的孩子只能从头遍历。
- 空数据导致遍历更慢。
(二)孩子表示法(顺序+链式存储)
- 孩子表示法:顺序存储各个节点,每个结点中保存孩子链表头指针。
- 优点:找孩子方便。
- 缺点:找父节点不方便。

struct CTNode{
int child; //孩子结点在数组中的位置
struct CTNode *next; //下一个孩子
};
typedef struct{
ElemType data;
struct CTNode *firstChild;//第一个孩子
}CTBox;
typedef struct{
CTBox nodes[MAX_TREE_SIZE];
int n,r; //结点数和根的位置
}CTree;
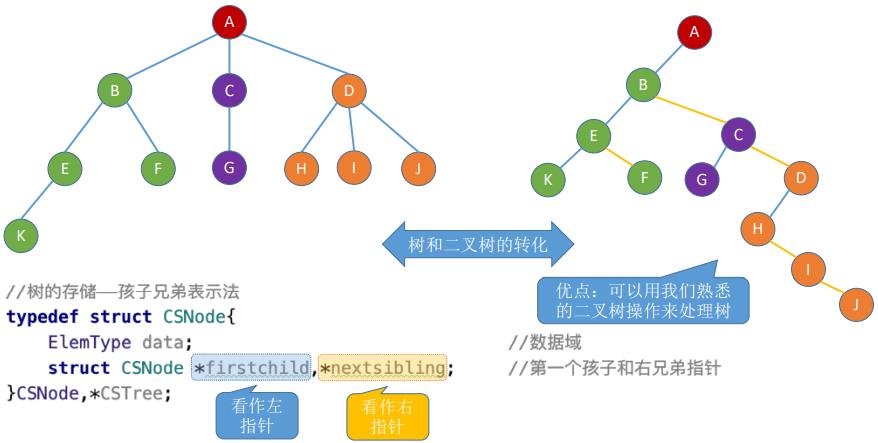
(三)❗❗❗孩子兄弟表示法(链式存储)❗❗❗
//树的存储——孩子兄弟表示法
typedef struct CSNode{
ElemType data; //数据域
struct CSNode *firstchild,*nextsibling; //第一个孩子和右兄弟指针
}CSNode, *CSTree;

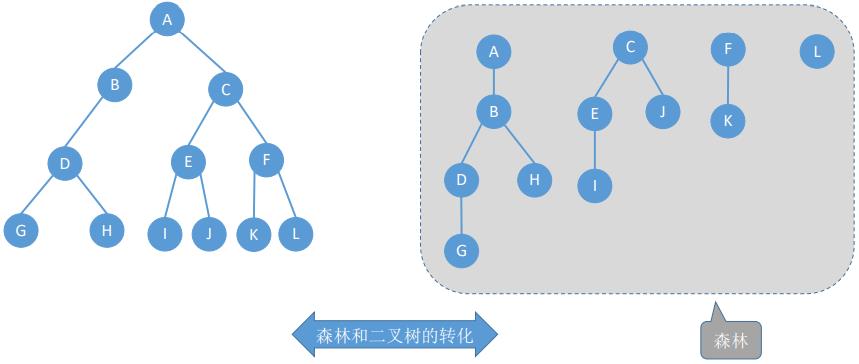
1. 森林和二叉树的转换
- 森林。森林是m(m≥0)棵互不相交的树的集合
- 本质:用二叉链表存储森林——左兄弟右孩子
- 森林中各个树的根节点之间视为兄弟关系。

二、树和森林的遍历
(一)树的先根遍历

//树的先根遍历
void PreOrder(TreeNode *R){
if(R != NULL){
visit(R); //访问根节点
while(R还有下一个子树T)
PreOrder(T); //先根遍历下一棵子树
}
}
(二)树的后根遍历
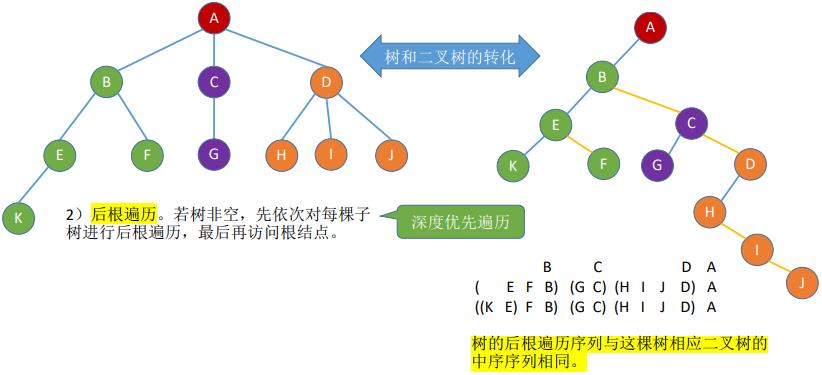
//树的后根遍历
void PostOrder(TreeNode *R){
if(R != NULL){
while(R还有下一个子树T)
PostOrder(T); //后根遍历下一棵子树
visit(R); //访问根节点
}
}
(三)树的层序遍历

(四)森林的先序遍历
- 森林。森林是m(m≥0)棵互不相交的树的集合。每棵树去掉根节点后,其各个子树又组成森林。


(五)森林的中序遍历

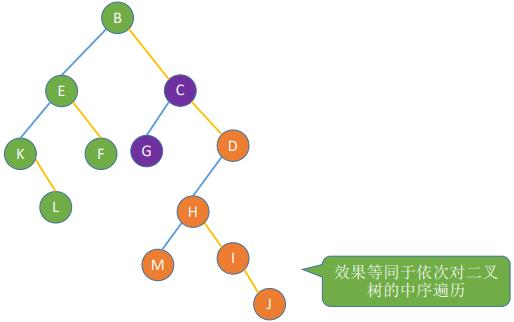
以上是关于树的存储结构以及树和森林的遍历(C语言)的主要内容,如果未能解决你的问题,请参考以下文章
数据结构学习笔记——树的存储结构以及树森林与二叉树之间的转换