C语言数据结构与算法----树和二叉树全面总结(中)
Posted 知心宝贝
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C语言数据结构与算法----树和二叉树全面总结(中)相关的知识,希望对你有一定的参考价值。
目录
一、前言
- 学习目标:掌握二叉树的先序、中序、后序、层次遍历,对于遍历算法的五个应用要求掌握、线索二叉树的基本结构和基本概念
- 重点:先序、中序、后序遍历、线索二叉树叶子结点判断、二叉链表存储
- 难点:线索二叉树(理解就行)
二、二叉树的遍历
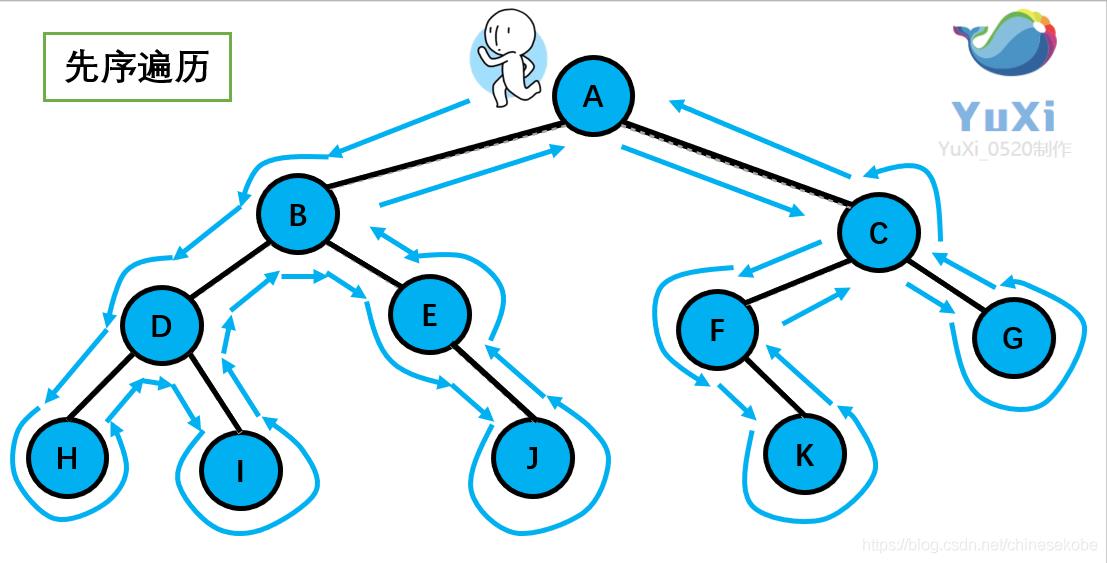
1.先序遍历
动态图:
 算法讲解:
算法讲解:
- 遍历顺序:根结点->左子树->右子树
- 动态图解:一个小人从根结点开始,围绕二叉树的外圈开始跑,依次输出序列
递归代码:
void PreOrder(BiTree root)
/*先序遍历二叉树, root为指向二叉树(或某一子树)根结点的指针*/
if (root!=NULL)
Visit(root ->data); /*访问根结点*/
PreOrder(root ->LChild); /*先序遍历左子树*/
PreOrder(root ->RChild); /*先序遍历右子树*/
2.中序遍历
动态图:

算法讲解:
- 遍历顺序:左子树->根结点->右子树
- 动态图解:中序遍历就像投影,将二叉树从最左侧到最右侧依次投影到同一水平线线,得到的序列就是二叉树的中序遍历
递归代码:
void InOrder(BiTree root)
/*中序遍历二叉树, root为指向二叉树(或某一子树)根结点的指针*/
if (root!=NULL)
InOrder(root ->LChild); /*中序遍历左子树*/
Visit(root ->data); /*访问根结点*/
InOrder(root ->RChild); /*中序遍历右子树*/
3.后序遍历
动态图:
算法讲解:
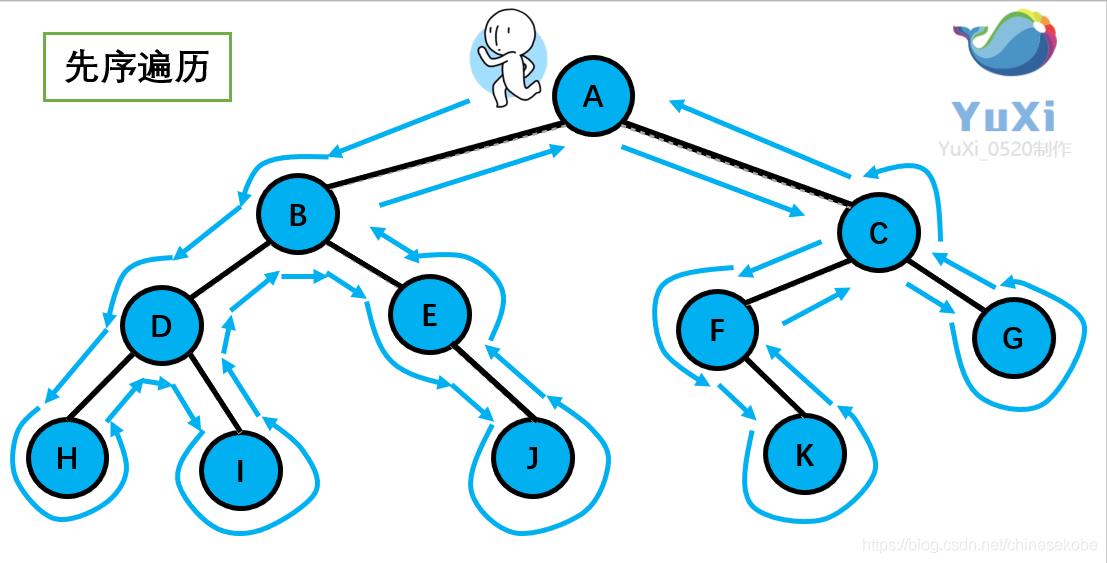
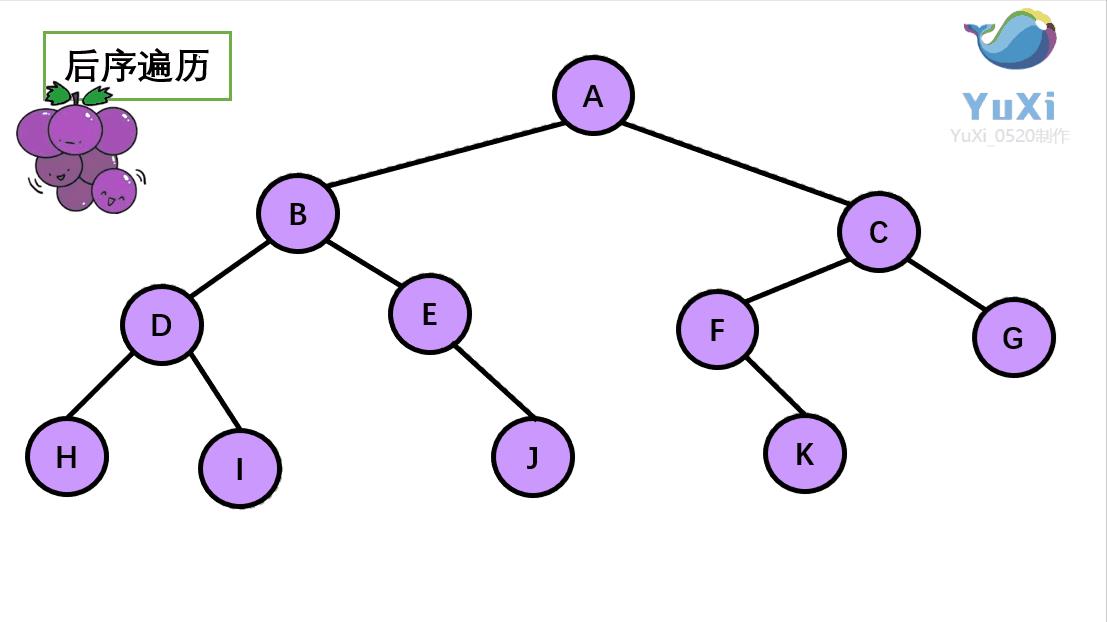
- 遍历顺序:左子树->右子树->根结点
- 动态图解:后序遍历也是按照先序遍历的顺序输出,不过后序遍历就像剪葡萄,只能一个个剪,不能让超过1个的葡萄一起掉下来。如上图中的B,剪去B后面的D、E、H、I、J都会掉下来,H剪去只会掉下H
递归代码:
void PostOrder(BiTree root)
/*后序遍历二叉树, root为指向二叉树(或某一子树)根结点的指针*/
if (root!=NULL)
PostOrder(root ->LChild); /*后序遍历左子树*/
PostOrder(root ->RChild); /*后序遍历右子树*/
Visit(root ->data); /*访问根结点*/
4.层次遍历
动态图:

算法讲解:
- 遍历顺序:一层一层开始遍历(算法不要求掌握)
三、遍历算法的应用
1.建立二叉链表存储的二叉树
void CreateBiTree(BiTree *bt)
//按“扩展先序遍历序列”建立二叉树的二叉链表的算法
char ch;
ch = getchar();
if(ch==‘.’) *bt=NULL; // 输入时以点号“. ”表示空结点。
else
*bt=(BiTree)malloc(sizeof(BiTNode)); //生成一个新结点
(*bt)->data=ch;
CreateBiTree(&((*bt)->LChild)); //生成左子树
CreateBiTree(&((*bt)->RChild)); //生成右子树
2.输出叶子结点
void PreOrder(BiTree root)
/*先序遍历二叉树, root为指向二叉树根结点的指针*/
if (root!=NULL)
if (root ->LChild==NULL && root ->RChild==NULL)
printf("%c ",root ->data); /*输出叶子结点*/
PreOrder(root ->LChild); /*先序遍历左子树*/
PreOrder(root ->RChild); /*先序遍历右子树*/
3.统计二叉树叶子结点数目
/* LeafCount保存叶子结点的数目的全局变量,调用之前初始化值为0 */
方法一:
void leaf_a(BiTree root)
if(root!=NULL)
leaf_a(root->LChild);
leaf_a(root->RChild);
if (root ->LChild==NULL && root ->RChild==NULL)
LeafCount++;
4.求二叉树高度
int PostTreeDepth(BiTree bt) /* 后序遍历求二叉树的高度递归算法 */
int hl,hr,max;
if(bt!=NULL)
hl=PostTreeDepth(bt->LChild); /* 求左子树的深度 */
hr=PostTreeDepth(bt->RChild); /* 求右子树的深度 */
max=hl>hr?hl:hr; /* 得到左、右子树深度较大者*/
return(max+1); /* 返回树的深度 */
else return(0); /* 如果是空树,则返回0 */
5.按树状打印二叉树
void PrintTree(BiTree bt,int nLayer) /* 按竖向树状打印的二叉树 */
if(bt == NULL) return;
PrintTree(bt->RChild,nLayer+1);
for(int i=0;i<nLayer;i++)
printf(" ");
printf("%c\\n",bt->data);
PrintTree(bt->LChild,nLayer+1);
四、线索二叉树
1.基本概念
- 前驱和后继:在二叉树先序、中序、后序、层次遍历之后得到的序列,前一个是前驱,后一个是后继
- 线索:指向前驱或后继结点的指针
- 线索化:对二叉树进行某种遍历次序,使之变成线索二叉树的过程
- 线索二叉树:加上线索的二叉链表
2.基本结构
- 孩子指针域:LChild指向左孩子,RChild指向右孩子
- 标志域Ltag:Ltag==1,表示LChild指向左孩子,Ltag==0表示LChild指向前驱
- 标志域Rtag:Rtag==1,表示RChild指向左孩子,Rtag==0表示RChild指向前驱
- 选择题表示结点p为叶子结点的是:p->Ltag==1&&p->Rtag==1
结构体:
typedef struct node
int data;
int ltag, rtag;
struct node *lchild, *rchild;
JD;
3.建立中序线索化二叉树
动态图:
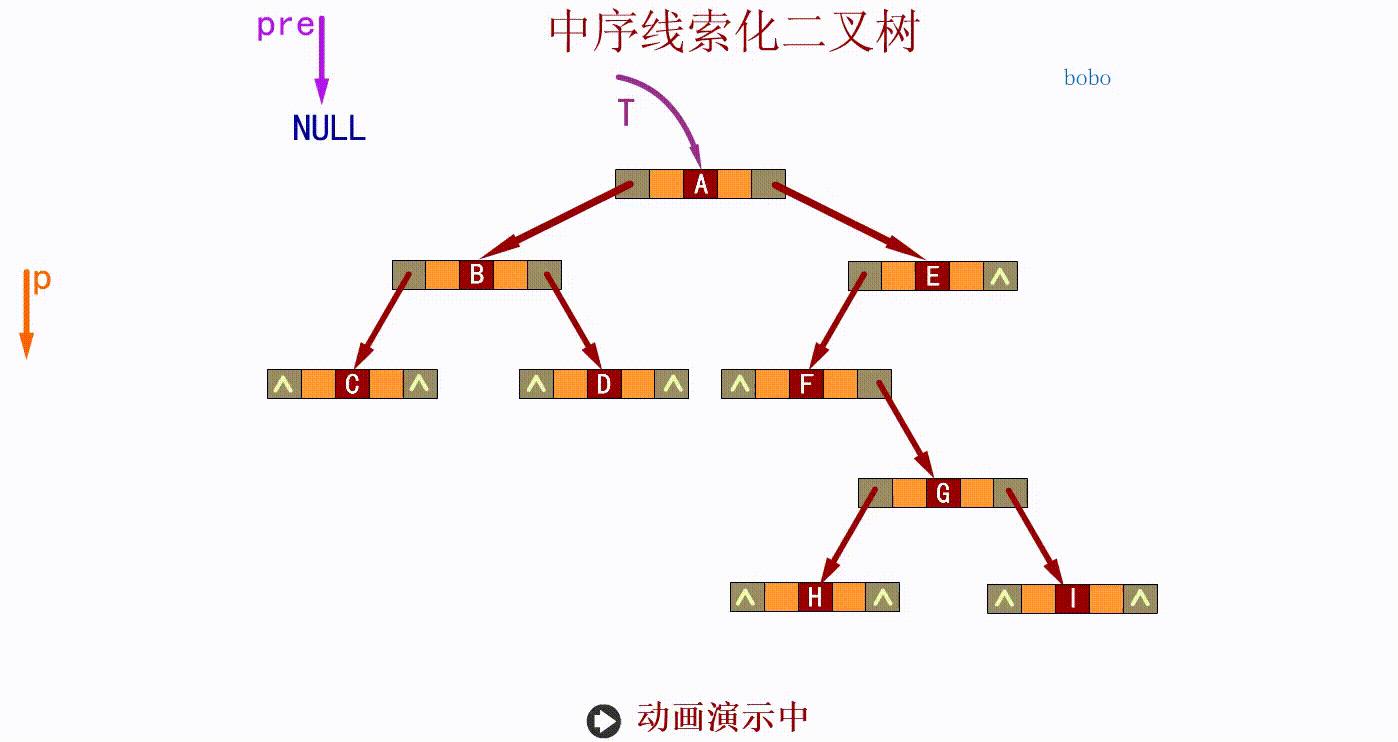
算法讲解:
- LTag=0, LChild指向根结点
- RTag=1, RChild指向遍历序列中最后一个结点
- 遍历序列中第一个结点的LChild域和最后一个结点的RChild域都指向根结点
代码:
void Inthread(BiTree root)
/* 对root所指的二叉树进行中序线索化,其中pre始终指向刚访问过的结点,其初值为NULL*/
if (root!=NULL)
Inthread(root->LChild); /* 线索化左子树 */
if (root->LChild==NULL)
root->Ltag=1;
root->LChild=pre; /*置前驱线索 */
if (pre!=NULL&& pre->RChild==NULL) /* 置后继线索 */
pre->RChild=root;
pre->Rtag=1;
pre=root;
Inthread(root->RChild); /*线索化右子树*/
文章遍历的动态图片参考:
【数据结构】理解二叉树的三种遍历--前序、中序、后序 +层序(简明易懂)
附录:
以上是关于C语言数据结构与算法----树和二叉树全面总结(中)的主要内容,如果未能解决你的问题,请参考以下文章