算法图解：广度优先搜索

Posted 2022-03-03 Thales_ZeeWay

广度优先搜索

对于图的搜索算法，有两种比较常见且使用广泛，分别hi是广度优先搜索（BFS）和深度优先搜索（DFS）。在这里，主要学习的广度优先搜索。广度优先搜索一般用来解决两个问题：

• 第一类问题：从节点A出发，是否有前往节点B的路径
• 第二类问题：从节点A出发，前往节点B的哪条路径最短

图的基础概念

我们这里先了解一下什么叫做图。

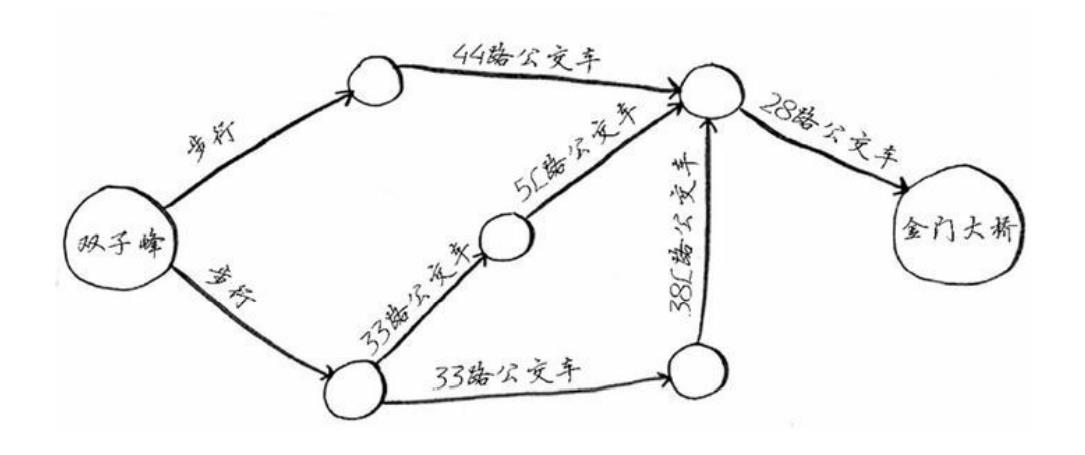
简单来说，我们可以把图理解为一张纸上的所有节点和连接节点的边。由于图的这个特性可以明显的看出各个节点的连接情况，所以图常常被用于模拟不同的东西是如何相连的。另外，图也分为有向图和无向图，两者的区别只在于连接节点的边是否具有箭头指向。单箭头的边表示只能单方向连通，无箭头的边表示可以双向连通。

第一类问题：从节点A出发，是否有前往节点B的路径

对于这类问题，我们可以用一个简单的例子来说明。

假设现在我有一间大别墅（当然不可能），我想把它卖出去，那我需要找一个合适的房产中介来帮我卖房子。为了知根知底，我会在我的人际关系圈中去寻找，找到合适的房产中介。

在这个问题中，我和我的朋友，还有我朋友的朋友等等。这些都可以看作是一个个节点，朋友间的联系，就可以看成是连接节点的边。那么我就可以这样来寻找搜素，先在我的朋友之中寻找，如果没有找到，就在我朋友的朋友中寻找，直到找到那个房产中介。

具体实现起来可以概况为：我先在一张纸上写下我朋友的名字，一个个查找过去，如果他不是中介，那么我就将他的朋友的名字写在名单上，等我将我的朋友们都找完再在这些人中寻找。

这样一直寻找搜索下去，我们就可以在我们广大的人际朋友圈之中寻找到我们需要的房产中介。换句话说，我们找到了从我到达房产中介的路径。

第二类问题：从节点A出发，前往节点B的哪条路径最短

这个问题其实可以看作是上一个问题的衍生。我们总是会趋向于和自己的朋友合作，而不是和朋友的朋友合作对吧。（就算被坑了，也可以直接肛他屁眼~~）

第二类问题的实现过程和第一类问题的实现是大致的。只是在名单中添加名字的时候，我们应该采用一种顺序添加的方法，也就是将后来的名字添加在名单的尾部，因为他们都不是我们的直接朋友，需要等我们先把直接朋友查找完再去考虑查找。（同时，也只有顺序添加可以实现这样的目的）

那么对于这个名单，我们可以使用特殊的数据结构来实现：队列。队列是一种特殊的数据结构，它的特点是先进先出，后进后出（其实也就和我们平时在超市排队一个道理），和栈是相反的。

如此一来，只要我们找到了房产中介，也就得到了相应的最短路径。

有一点需要注意的是，因为会存在你的一个朋友A和另外一个朋友B也是朋友的情况，如果不加控制，那么就会一直重复的查找这两个朋友。（具体的情况会像这样：查找A，A不是中介，A有一个朋友B，查找B，B不是中介，B有一个朋友A，查找A，A不是中介......）所以呢，我们需要在查找名单之外，再使用一个名单来存放那些已经查找过的人，在这个名单中的名字，将不会再被添加到查找名单中。