[AGC049D] Convex Sequence

Posted Marsrayd

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[AGC049D] Convex Sequence相关的知识，希望对你有一定的参考价值。

[AGC049D] Convex Sequence

给定整数 \\(n\\) 和 \\(m\\)，问有多少个长为 \\(n\\) 的非负整数数列 \\(A\\)，满足以下条件：

  • \\(A_1+A_2+\\ldots+A_n = m\\)
  • 对任意 \\(i(2 \\leq i \\leq N-1)\\) ，都有 \\(2A_i \\leq A_i-1 + A_i+1\\)

答案对 \\(10^9+7\\) 取模。

\\(\\textttdata range\\)：\\(n,m\\le 100000\\)。

通过题目和

Convex Sets and Convex functions

文章目录

第3章 Convex Sets and Convex functions

凸优化问题的定义

凸集的定义：

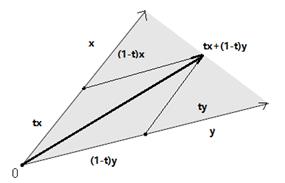
定义：给定一个集合 C ⊆ R n C \\subseteq \\mathbbR^n C⊆Rn,满足下列条件则称为凸集： x , y ∈ C ⇒ t x + ( 1 − t ) y ∈ C x,y \\in C \\Rightarrow tx+(1-t)y \\in C x,y∈C⇒tx+(1−t)y∈C 对于任意的 0 ≤ t ≤ 1 0≤t≤1 0≤t≤1


直观上看，可以利用下图帮助理解，假定我们的变量在二维空间中，x,y为二维空间变量，黑体线代表的向量为tx+(1−t)y，t取值范围为[0,1]，那么无论t怎么变化，向量tx+(1−t)y总会落在x和y张成的集合空间中。[3]

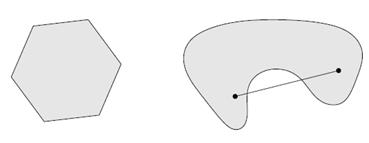
那么从定义出发，我们也能知道非凸集的情况，下图左侧为凸集，右图为非凸集。一句话来概括凸集就是集合内任意两点间连线依旧在集合内。

convex hull（凸包） 定义：


给定集合内的任意k个元素 x 1 , . . . , x k ∈ R n x_1,...,x_k \\in \\mathbbR^n x1​,...,xk​∈Rn,任意的线性组合形式： θ 1 x 1 + . . . + θ k x k , θ i ≥ 0 , ∑ i = 1 k θ i = 1 \\theta_1 x_1+...+\\theta_k x_k,\\theta_i \\geq 0, \\sum_i=1^k\\theta_i=1 θ1​x1​+...+θk​xk​,θi​≥0,∑i=1k​θi​=1，称之为集合的convex hull,表示为 c o n v ( C ) conv(C) conv(C)。convex hull总是凸的。可以直观认为凸包就是最外围的元素所围成的集合外壳，下图是两个凸包的例子：

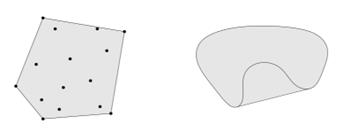
一些凸集的examples：



锥（Cone）和凸锥（Convex Cone）的定义


范数锥(Norm cone): ( x , t ) : ∣ ∣ x ∣ ∣ ≤ t \\left \\(x,t):||x|| \\leq t \\right \\ (x,t):∣∣x∣∣≤t，对于一范数和二范数成立。下图取定不同的t做出了三维情况下的图

（讨论：这里我感觉用字母 t t t有一些歧义，和上面定义中的 t t t不是一个含义。范数锥中的 t t t是定义域中的一个维度变量；而上面锥定义中的 t t t是表示一个常数）：

凸集的性质：

  • 可分离超平面理论（Separating hyperplane theorem）：两个不相交的凸集总存在一个超平面能将两者分离，如果 C ⋂ D = ∅ C⋂D=∅ C⋂D=∅,那么总存在着a,b使得有: C ⊆ x : a T x ≤ b C \\subseteq \\left \\x:a^Tx \\leq b \\right \\ C⊆x:aTx≤b， D ⊆ x : a T x ≥ b D \\subseteq \\left \\x:a^Tx \\geq b \\right \\ D⊆x:aTx≥b

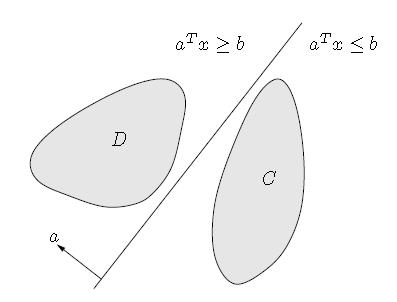
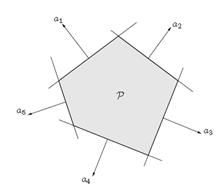
  • 支撑超平面理论(Supporting hyperplane theorem):凸集边界上的一点必然存在一个支撑超平面穿过该点，即如果C都是非空凸集，
    x 0 ∈ b o u n d ( C ) x_0 \\in bound(C) x0​∈bound(C)，那么必然存在一个超平面a，使得, C ⊆ x : a T x ≤ a T x 0 C \\subseteq \\left \\x:a^Tx \\leq a^T x_0 \\right \\ C⊆x:aTx≤aTx0​。如下图：

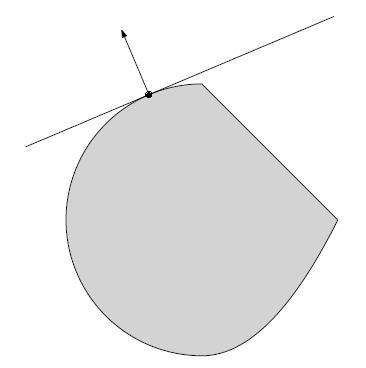
保凸操作：


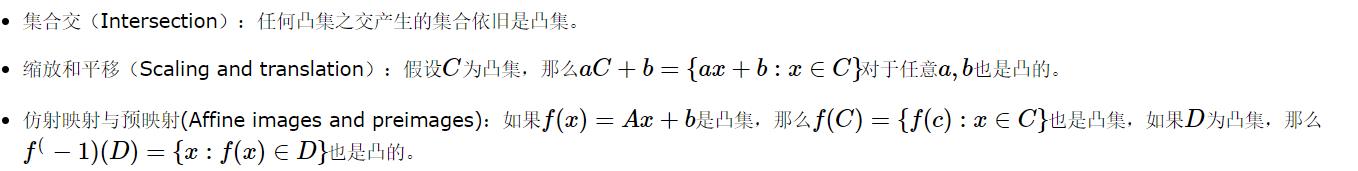
（上面是 f − 1 ( D ) f^-1(D) f−1(D)，因为借用了[3]的截图，就不重新打了。）

一个例子：

这一章都是一些概念，看的有点晕，哈哈。下面看一下一个证明的例子：

给定一系列的 n × n n\\times n n×n的对称矩阵，有一种线性矩阵不等式如下，其中 x ∈ R k x \\in R^k x∈Rk。证明： x x x组成的集合C是凸集。

证明过程思路上面写了：只要根据前面提过的凸集定义去证明就行了。如果有 x , y ∈ C x,y \\in C x,y∈C，只要证明 t x + ( 1 − t ) y ∈ C tx+(1-t)y \\in C tx+(1−t)y∈C，
其中 0 ≤ t ≤ 1 0\\leq t \\leq 1 0≤t≤1，就可以了。根据题目，我们可以知道：
t v T B v − ∑ i = 1 k t x i v T A i v ≥ 0 ( 1 − t ) v T B v − ∑ i = 1 k ( 1 − t ) y i v T A i v ≥ 0 tv^T B v - \\sum_i=1^ktx_iv^TA_i v \\geq 0 \\\\ (1-t)v^T B v - \\sum_i=1^k(1-t)y_iv^TA_i v \\geq 0 tvTBv−i=1∑k​txi​vTAi​v≥0(1−t)vTBv−i=1∑k​(1−t)yi​vTAi​v≥0

然后我们可以推出

v T ( B − ∑ i = 1 k ( t x i + ( 1 − t ) y i ) A i ) v = v T B v − ∑ i = 1 k ( t x i + ( 1 − t ) y i ) v T A i v = ( t + ( 1 − t ) ) v T B v − ∑ i = 1 k ( t x i + ( 1 − t ) y i ) v T A i v ≥ 0 v^T \\left(B - \\sum_i=1^k(tx_i + (1-t)y_i)A_i \\right) v \\\\ = v^T B v - \\sum_i=1^k(tx_i + (1-t)y_i)v^TA_i v \\\\ = (t + (1-t))v^T B v - \\sum_i=1^k(tx_i + (1-t)y_i)v^TA_i v \\geq 0\\\\ vT(B−i=1∑k​(txi​+(1−t)yi​)Ai​)v=vTBv−i=1∑以上是关于[AGC049D] Convex Sequence的主要内容，如果未能解决你的问题，请参考以下文章

AtCoder AGC031D A Sequence of Permutations (群论置换快速幂)

[AGC003E]Sequential operations on Sequence

agc003E Sequential operations on Sequence

Agc003_E Sequential operations on Sequence

Convex Sets and Convex functions

Convex Sets and Convex functions