主成分分析（PCA），用Matlab和SAS、SPSS结果不一样，后二者一样。但三者的特征值一样，特征向量正负不一

Posted 2023-05-16

特征向量的结果：
原始数据：（18样本*6变量）
92 77 80 95 99 126
97 75 77 80 95 125
95 80 70 78 89 120
75 75 73 88 98 110
92 68 72 79 88 113
90 85 80 70 78 103
72 93 75 77 80 100
88 70 76 72 81 102
64 70 69 85 93 105
70 73 70 87 84 100
78 69 75 73 89 97
78 72 71 68 75 96
75 64 63 76 73 92
84 66 77 55 65 76
70 64 51 60 67 88
58 72 75 62 52 75
82 73 40 50 48 61
45 65 42 47 43 60

三种方法特征根都是一样的：
3.9829 0.8314 0.6630 0.4120 0.0640 0.0466

但特征向量不一样：
SAS、SPSS的结果（特征向量矩阵）：
0.342794 0.071053 0.882724 0.118374 0.287588 0.039016
0.253554 0.914051 -.200006 0.233780 -.020130 0.071834
0.403902 0.112564 -.045051 -.906119 0.006436 -.032695
0.446693 -.234003 -.405320 0.201942 0.711506 -.185481
0.472785 -.263329 -.120036 0.154394 -.296973 0.762033 0.481670 -.150637 0.008555 0.213692 -.567814 -.614127
Matlab的结果（特征向量矩阵）：
-0.3428 0.0711 -0.8827 0.1184 0.2876 0.0390
-0.2536 0.9141 0.2000 0.2338 -0.0201 0.0718
-0.4039 0.1126 0.0451 -0.9061 0.0064 -0.0327
-0.4467 -0.2340 0.4053 0.2019 0.7115 -0.1855
-0.4728 -0.2633 0.1200 0.1544 -0.2970 0.7620
-0.4817 -0.1506 -0.0086 0.2137 -0.5678 -0.6141

第一主成分和第三主成分的特征向量的正负号正好是相反的。从结果直观分析，sas、spss的结果应该更好，即，第一主成分的特征向量理论上应该是正的。

为什么有如此差异？有什么方法可以解决？

谢谢！

主成份分析本质上是一种降维技术，要将多个变量通过旋转在少数维度（最好是2个）上表示出来，并据此分类。但是旋转的方法不同，投射出来的结果也是不一样的，因此你会看到特征向量数值绝对值相同，但符号相反。就好比一种旋转方法将点投影到了X轴之上，而另一种方法恰好投影到了X轴之下。在使用时你只要能确定变量和主成份之间的关系就可以了，解释时用最方便解释得结果。 参考技术A 映射关系不同导致，不影响的，关键是特征值的累积置贡献率达到一定值就可以取这几个做主特征值了。

图像识别基于主成分分析PCA实现视频人脸识别matlab源码

逐步解释PCA

第一步：标准化

此步骤的目的是标准化输入数据集，使数据成比例缩小。

更确切地说，在使用PCA之前必须标准化数据的原因是PCA方法对初始变量的方差非常敏感。也就是说，如果初始变量的范围之间存在较大差异，那么范围较大的变量占的比重较大，和较小的变量相比（例如，范围介于0和100之间的变量较0到1之间的变量会占较大比重），这将导致主成分的偏差。通过将数据转换为同样的比例可以防止这个问题。

在数学上，可以通过减去平均值并除以每个变量的标准偏差来完成。

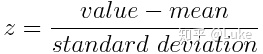
标准化

标准化完成后，所有变量将转换为相同的范围：[0,1]。

 

第二步：计算协方差矩阵

此步骤的目的是了解输入数据集的变量相对于彼此平均值变化，换句话说，查看它们是否存在关系。因为有时候，变量由于高度相关，这样就会包含冗余信息。因此，为了识别变量的相关性，我们计算协方差矩阵。

协方差矩阵是p×p对称矩阵（其中p是维数），变量与变量之间的协方差作为矩阵元素。例如，对于具有3个变量x，y和z的三维数据集，协方差矩阵是以下的3×3矩阵：

 

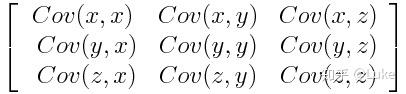
协方差矩阵变量有什么用呢？

实际上协方差的符号起作用：

• 如果是正的话：两个变量一起增加或减少（相关），
• 如果是负的话：当一个变量增加时，另一个变量减少（不相关）

现在，我们知道协方差矩阵不仅仅是一个矩阵，而是展示变量相关性的矩阵，让我们进入下一步。

 

第三步：计算协方差矩阵的特征向量和特征值以识别主成分

特征向量和特征值是我们需要从协方差矩阵计算的线性代数概念，以便确定数据的主要成分。 在开始解释这些概念之前，让我们首先理解主成分的含义。

主成分是新变量，是初始变量的线性组合。这些组合以新变量（即主成分）不相关的方式完成，并且初始变量内的大部分信息被压缩或压缩到第一组分中。比如，10维数据提供10个主要组件，但PCA尝试在第一个组件中获取最大可能信息，然后在第二个组件中获得最大剩余信息，依此类推。

如果你有一个10维数据，你最终会得到类似下面的图中显示的内容，其中第一个主要组件包含原始数据集的大部分信息，而最后一个只携带少数几个。因此，以这种方式组织信息，可以在不丢失太多信息的情况下减少维度，并通过丢弃携带较少信息的组件来实现这一点。

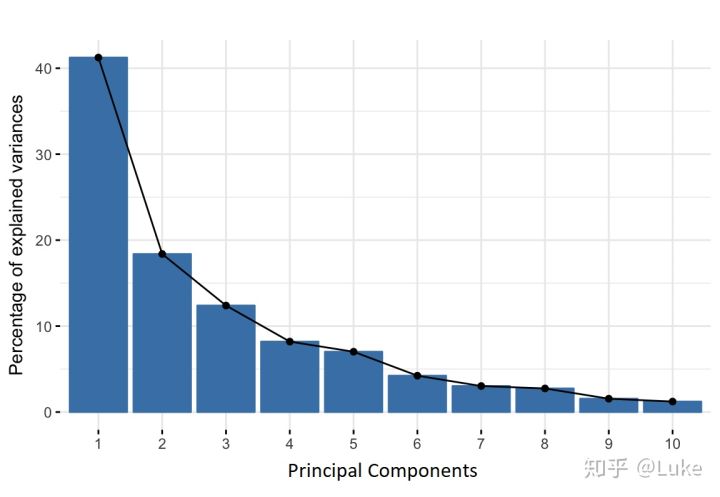
每个主成分方差所占的比重

主成分不是很好解释，并且对我们没有任何实际意义，因为它们被构造为初始成分的线性组合。 从几何学上讲，主成分表示解释最大方差量的数据的方向，也就是说，捕获数据的大部分信息的线。这里方差和信息之间的关系是，线所承载的方差越大，数据点沿着它的分散越大，沿着线的色散越大，它所具有的信息就越多。简单地说，只需将主成分视为新轴，然后从这个轴查看和评估数据。

PCA怎么构建主成分？

由于数据中存在与变量一样多的主成分，因此主成分以第一主成分占数据集中最大可能方差的方式构造。例如，假设我们的数据集的散点图如下所示，我们可以猜出第一个主成分吗？它大致是与紫色标记匹配的线，因为它穿过原点，并且它是点（红点）的投影最分散的线。或者从数学上讲，它是最大化方差的线（从投影点（红点）到原点的平方距离的平均值）。

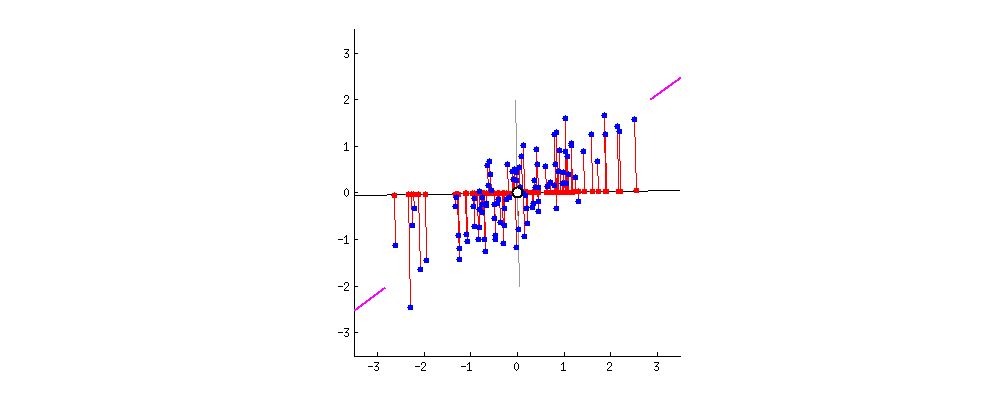
第二主成分以相同的方式计算，条件是它与第一主成分不相关（即垂直），并且它占下一个最高方差。这一直持续到计算出总共p个主成分，等于原始变量数。 现在我们理解了主成分的含义，让我们回到特征向量和特征值。你首先需要知道的是它们总是成对出现，因此每个特征向量都有一个特征值。它们的数量等于数据的维数。例如，对于三维数据集，存在3个变量，因此存在3个具有3个对应特征值的特征向量。 协方差矩阵的特征向量实际上是方差最多的轴的方向（大多数信息），我们称之为主成分。并且特征值只是附加到特征向量的系数，它们给出了每个主成分中携带的方差量。 通过按特征值的顺序对特征向量进行排序，从最高到最低，按重要性顺序得到主要成分。

 

% Create a cascade detector object.
faceDetector = vision.CascadeObjectDetector();

% Read a video frame and run the detector.
videoFileReader = vision.VideoFileReader('visionface.avi');
videoFrame      = step(videoFileReader);
bbox            = step(faceDetector, videoFrame);

% Draw the returned bounding box around the detected face.
videoOut = insertObjectAnnotation(videoFrame,'rectangle',bbox,'Face');
%%videoOut = insertObjectAnnotation( double(videoFrame), 'rectangle', bbox, 'Face');
vision.ShapeInserter
figure, imshow(videoOut), title('Detected face');

% Get the skin tone information by extracting the Hue from the video frame
% converted to the HSV color space.
[hueChannel,~,~] = rgb2hsv(videoFrame);

% Display the Hue Channel data and draw the bounding box around the face.
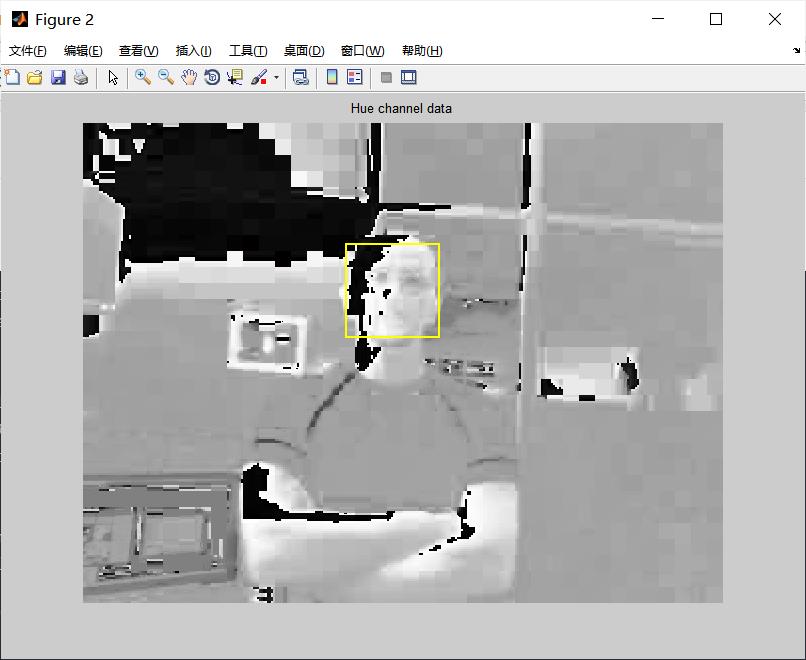
figure, imshow(hueChannel), title('Hue channel data');
rectangle('Position',bbox(1,:),'LineWidth',2,'EdgeColor',[1 1 0])

% Detect the nose within the face region. The nose provides a more accurate
% measure of the skin tone because it does not contain any background


end

% Release resources
release(videoFileReader);
release(videoPlayer);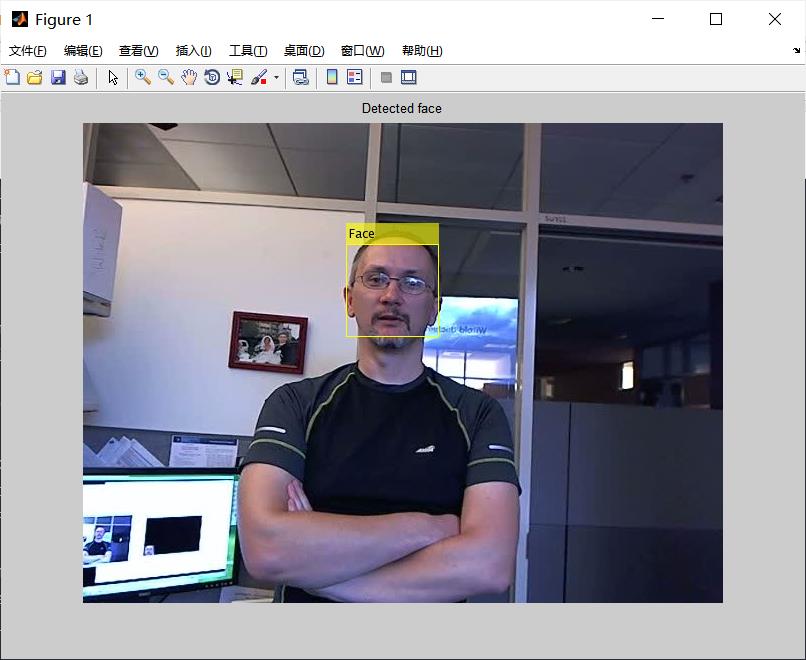

完整代码或者仿真咨询添加QQ1575304183