傅里叶变化
- 含义: 与时域对比,傅里叶变化更关心的是在频率域所发生的事情
傅里叶变化的作用
- 高频 变化剧烈的灰度分量 比如图像边界
- 低频 变化缓慢的灰度分量 灰度均匀区域
滤波
- 低通滤波器: 只保留低频信息 边界会模糊
- 高通滤波器: 只保留高频信息 增强图像细节
示例
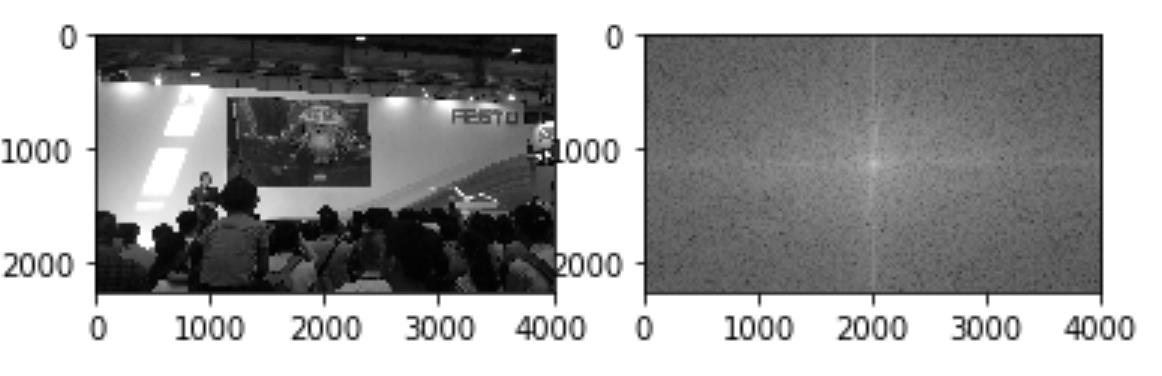
img = cv2.imread(r"E:\\2019PythonProject\\OpencvTest\\123.jpg",0)
# 图像数据要转换成float32
img_float32 = np.float32(img)
#进行傅里叶变换
dft = cv2.dft(img_float32,flags = cv2.DFT_COMPLEX_OUTPUT)
# 将低频信息转换至图像中心
dft_shift = np.fft.fftshift(dft)
# 傅里叶变换后的数据是由实部虚部构成的,需要进行转换成图像格式才能显示(0,255)
magnitude = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
plt.subplot(121),plt.imshow(img,cmap = \'gray\')
plt.subplot(122),plt.imshow(magnitude,cmap=\'gray\')
plt.show()
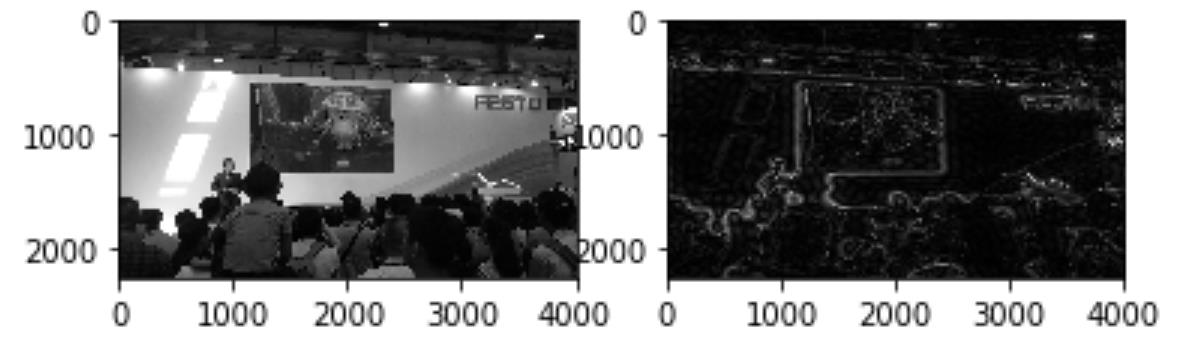
# 获取图像尺寸 与 中心坐标
rows,cols = img.shape
crow,ccol = int(rows/2),int(cols/2)
# 创建高通掩码
mask = np.ones((rows,cols,2),np.uint8)
mask_size = 20
mask[crow - mask_size:crow +mask_size, ccol -mask_size:ccol+mask_size] = 0
# 掩码与傅里叶图像按位相乘 去除低频区域
fshift = dft_shift * mask
# 之前把低频转换到了图像中间,现在需要重新转换回去
f_ishift = np.fft.ifftshift(fshift)
# 傅里叶逆变换
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
plt.subplot(121),plt.imshow(img,cmap = \'gray\')
plt.subplot(122),plt.imshow(img_back,cmap=\'gray\')
plt.show()