采样定理的定理历程

Posted 2023-04-25

1924年奈奎斯特(Nyquist)推导出在理想低通信道的最高码元传输速率的公式。
1928年美国电信工程师H.奈奎斯特推出采样定理，因此称为奈奎斯特采样定理。
1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理，因此在苏联文献中称为科捷利尼科夫采样定理。
1948年信息论的创始人C.E.香农对这一定理加以明确地说明并正式作为定理引用，因此在许多文献中又称为香农采样定理。采样定理有许多表述形式，但最基本的表述方式是时域采样定理和频域采样定理。
采样定理在数字式遥测系统、时分制遥测系统、信息处理、数字通信和采样控制理论等领域得到广泛的应用。

参考技术A 1、采样定理的定理历程为：
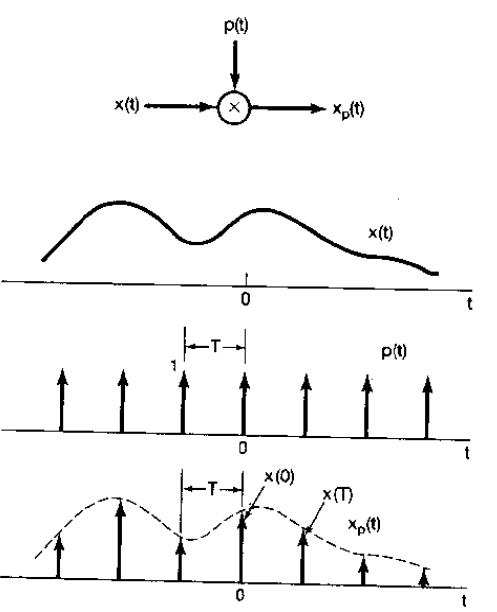
（1）1924年奈奎斯特推导出在理想低通信道的最高码元传输速率的公式；
（2）1928年美国电信工程师H.奈奎斯特推出采样定理，因此称为奈奎斯特采样定理；
（3）1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理，因此在苏联文献中称为科捷利尼科夫采样定理；
（4）1948年信息论的创始人C.E.香农对这一定理加以明确地说明并正式作为定理引用，因此在许多文献中又称为香农采样定理；采样定理有许多表述形式，但最基本的表述方式是时域采样定理和频域采样定理。
2、采样定理是美国电信工程师H.奈奎斯特在1928年提出的，采样定理说明采样频率与信号频谱之间的关系，是连续信号离散化的基本依据。
3、在进行模拟/数字信号的转换过程中，当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，一般实际应用中保证采样频率为信号最高频率的2.56～4倍；采样定理又称奈奎斯特定理。

转载：奈奎斯特采样定理

原文：http://xilinx.eetrend.com/article/10399

现实世界接触到的诸如电信号、光信号、声音信号等这些信号都是随时间连续变化的，称之为连续信号。但对于计算机来说，处理这些连续的信号显然是无能为力，要使计算机能够识别、计算、处理这些连续信号就必须将其转化为离散信号，将连续信号转换为离散信号的过程就叫采样。常用的mp3、数码照片、视频等都是经过了采样，才能应用于计算机上。
采样后，计算机得到的是离散的点，用这些离散的点来代替连续的线就势必会产生误差，那么这个误差是不是在容许的范围内，根据采样得到离散的点能不能还原出连续的信号？

奈奎斯特采样定理
奈奎斯特采样定理解释了采样率和所测信号频率之间的关系。 阐述了采样率fs必须大于被测信号感兴趣最高频率分量的两倍。 该频率通常被称为奈奎斯特频率f_N。

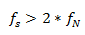
为更好理解其原因，让我们来看看不同速率测量的正弦波。 情况A，频率f的正弦波以同一频率采样。 这些采样标记在原始信号的左侧，在右侧构建时，信号错误地显示为恒定直流电压。 情况B，采样率是信号频率的两倍。 现在信号显示为三角波。 这种情况下，f等于奈奎斯特频率，这也是特定采样频率下为了避免混叠而允许的最高频率分量。 情况C，采样率是4f/3。

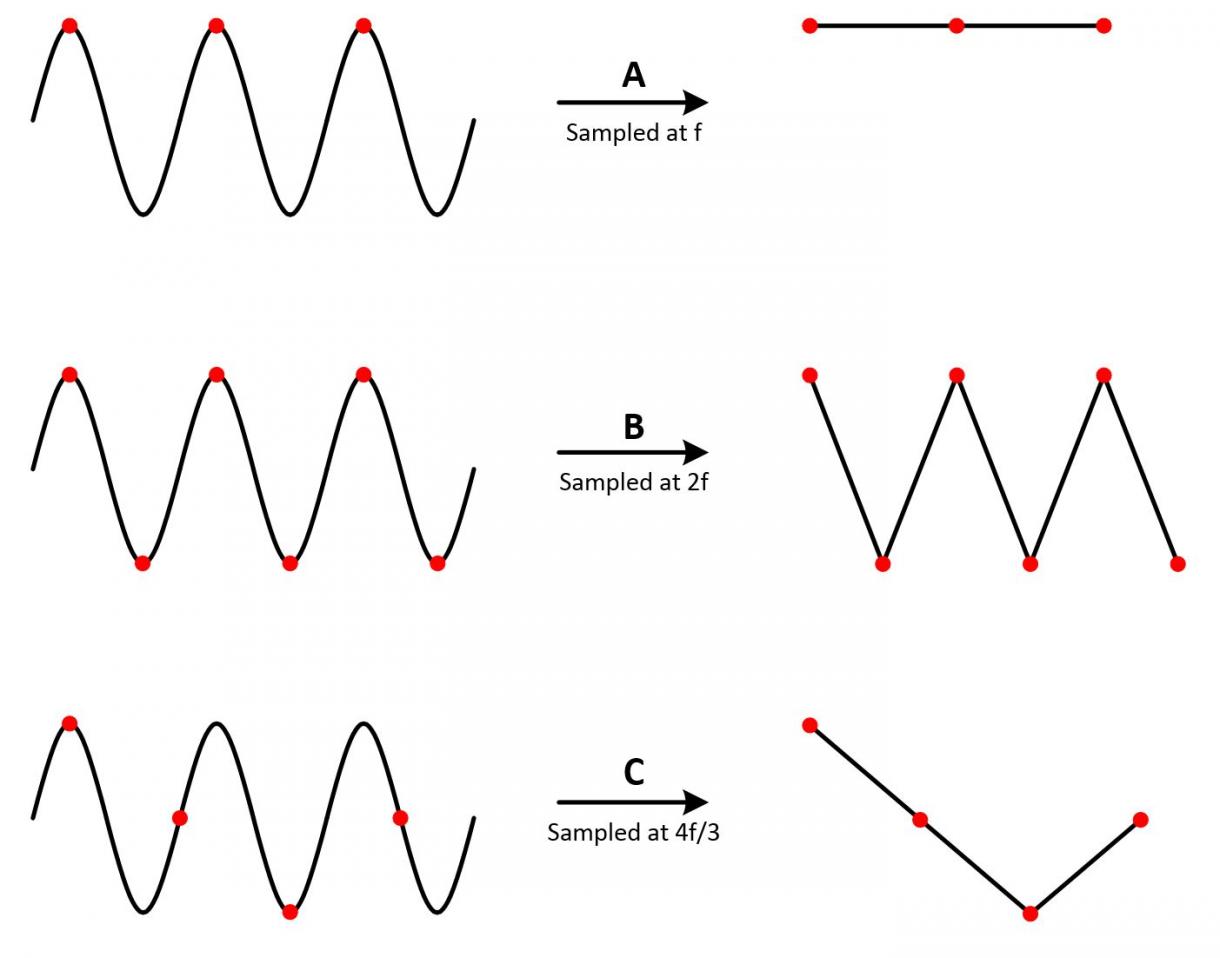
采样率过低会造成波形重构不准确。因此，为了无失真地恢复原波形信号，采样率fs必须大于被测信号感兴趣最高频率分量的两倍。 通常希望采样率大于信号频率约五倍。

混叠
如需按一定速率采样以避免混叠，那么混叠到底是什么？ 如果信号的采样率低于两倍奈奎斯特频率，采样数据中就会出现虚假的低频成分。 这种现象便称为混叠。 

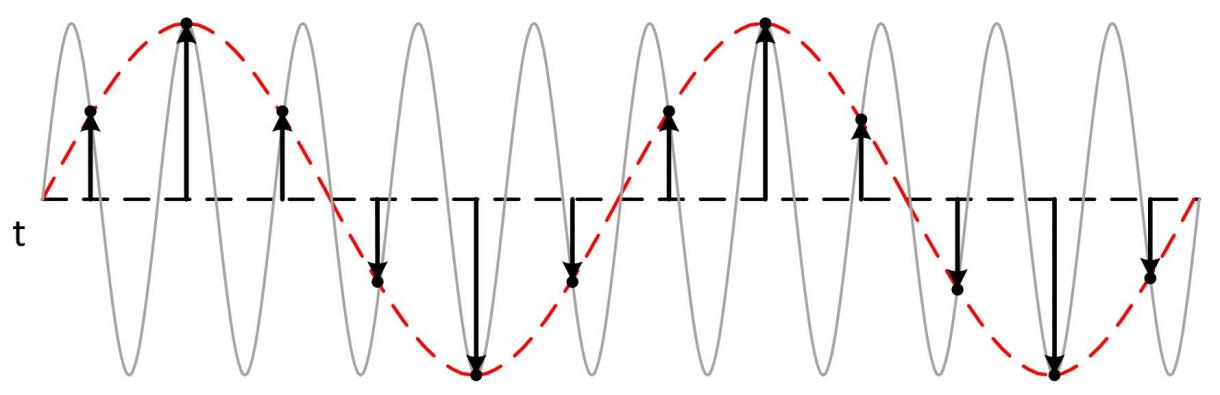
 混叠发生在采样率过低的时候，产生不精确的波形显示。