简述奈奎斯特时域抽样定理?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了简述奈奎斯特时域抽样定理?相关的知识,希望对你有一定的参考价值。
百度百科有奈奎斯特抽样定理,我不知道这两个是不是一回事
奈奎斯特抽样定理指若频带宽度有限的,要从抽样信号中无失真地恢复原信号,抽样频率应大于2倍信号最高频率。抽样频率小于2倍频谱最高频率时,信号的频谱有混叠。
抽样频率大于2倍频谱最高频率时,信号的频谱无混叠。 参考技术A 采样定理是美国电信工程师H.奈奎斯特在1928年提出的,在数字信号处理领域中,采样定理是连续时间信号(通常称为“模拟信号”)和离散时间信号(通常称为“数字信号”)之间的基本桥梁。该定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。 它为采样率建立了一个足够的条件,该采样率允许离散采样序列从有限带宽的连续时间信号中捕获所有信息。 参考技术B w他的问题我回答不了不好意思哦 参考技术C 这个可以去百度一下,看看有没有相关的知识。
数字信号处理4:采样定理
文章目录
采样定理又称奈奎斯特定理,它规定了连续信号抽样成为离散信号时的采样率与信号最大频率之间的关系,那就是:
对于连续信号 x ( t ) x(t) x(t)进行抽样时,抽样信号的最小频率 p ( t ) p(t) p(t)的频率要大于 x ( t ) x(t) x(t)的最大频率的2倍,采样得出的信号 x [ n ] x[n] x[n]才能还原出原始信号 x ( t ) x(t) x(t)。
这一点其实容易想明白,比如下面三个信号:
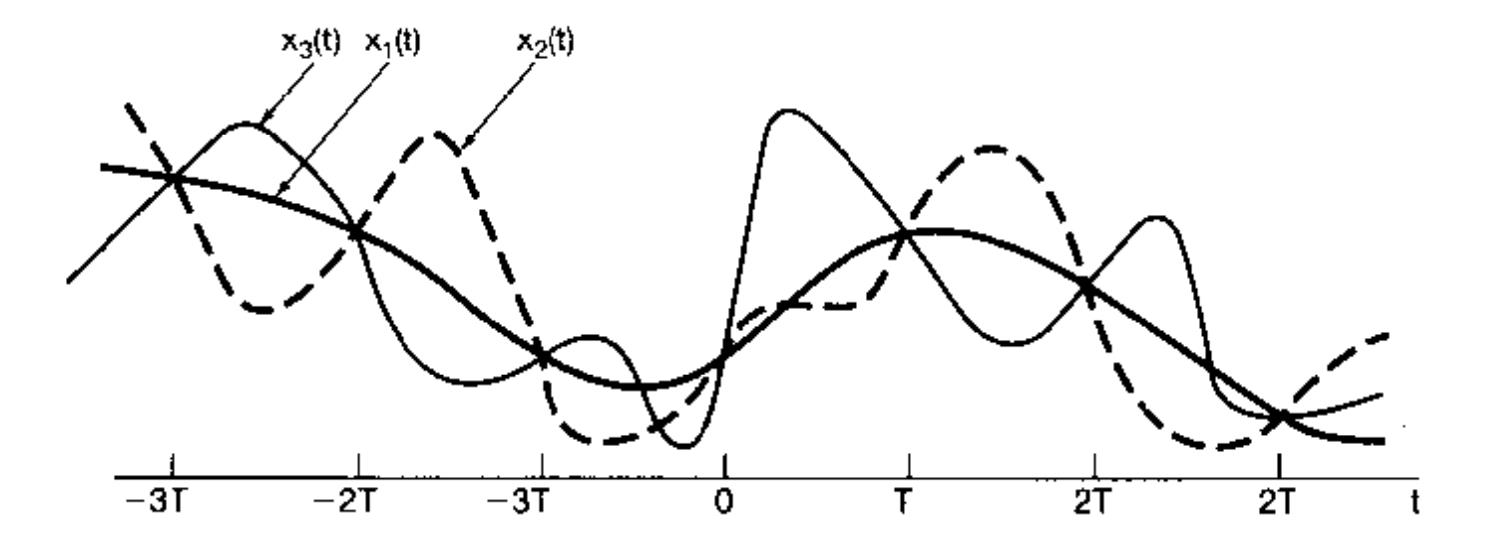
如果在T的整数倍处对三个信号采样,你会发现采样出的信号是完全一致的,这就导致你无法还原原始信号。因此,我们要明确采样频率和原信号的中包含的最高频率分量的关系。
通常来说,我们对于一个连续信号采样时,是截取
x
(
t
)
x(t)
x(t)在某一时刻的值,因此不妨将整个采样过程看做
x
(
t
)
x(t)
x(t)与
p
(
t
)
p(t)
p(t)的乘积,其中
p
(
t
)
p(t)
p(t)是梳妆函数,它是一系列冲激信号的延时叠加:
p
(
t
)
=
∑
n
=
−
∞
+
∞
δ
(
t
−
n
T
)
p(t) = \\sum_n = -\\infty^+\\infty \\delta(t-nT)
p(t)=n=−∞∑+∞δ(t−nT)
它的时域图像如下:
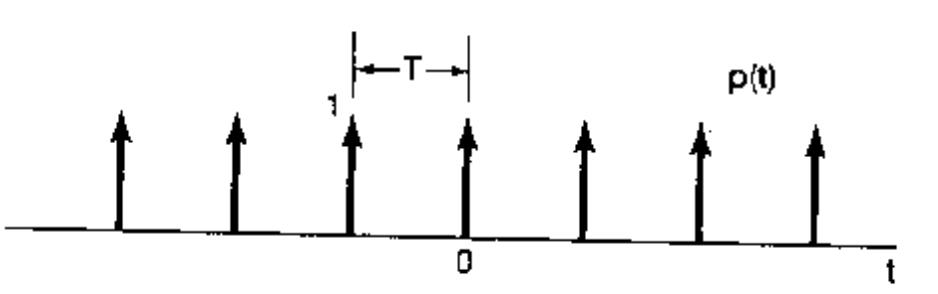
对它做傅里叶变换得到频域图像如下:
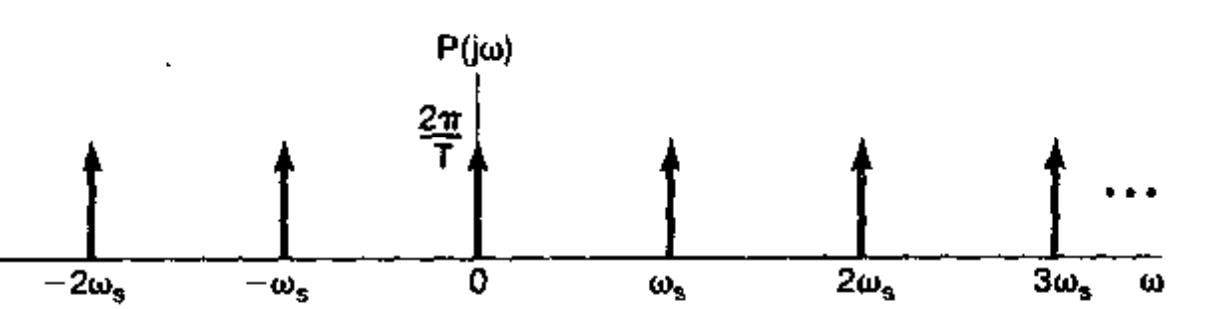
对应的表达式为
P ( j w ) = ∑ k = − ∞ + ∞ δ ( w − k w s ) P(jw) = \\sum_k=-\\infty^+\\infty\\delta(w - kw_s) P(jw)=k=−∞∑+∞δ(w−kws)
而对于
x
(
t
)
x(t)
x(t),我们需要假设它是一个带限信号,意味着它在频率上是有界的(否则就会发生频谱混叠)。它的频域图像如下:
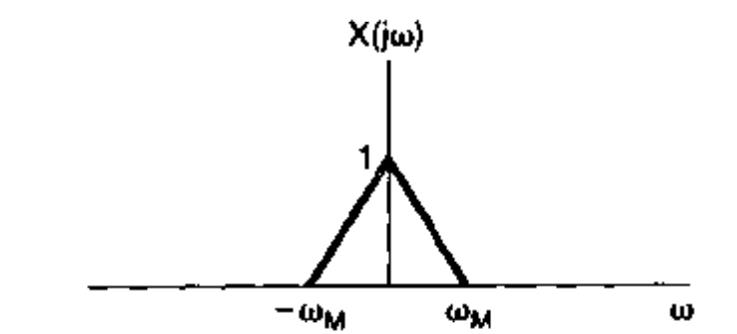
以上就是我们对输入信号 x ( t ) x(t) x(t)和采样信号 p ( t ) p(t) p(t)的直观认识,接下来推导采样定理。
1. 卷积定理
之前我们有说过,时域卷积等于频域相乘,频域相乘等于时域卷积。这个结论对于我们推导采样定理以及建立对傅里叶变换后的频域的认识非常重要。因此先推导这个结论。
假设有信号
y
(
t
)
=
x
(
t
)
∗
h
(
t
)
=
∫
−
∞
+
∞
x
(
τ
)
h
(
t
−
τ
)
d
τ
y(t) = x(t) * h(t) = \\int_-\\infty^+\\inftyx(\\tau)h(t-\\tau)d\\tau
y(t)=x(t)∗h(t)=∫−∞+∞x(τ)h(t−τ)dτ
直接对
y
(
t
)
y(t)
y(t)做傅里叶变换:
Y
(
j
w
)
=
∫
−
∞
+
∞
[
∫
−
∞
+
∞
x
(
τ
)
h
(
t
−
τ
)
d
τ
]
e
−
j
w
t
d
t
Y(jw) = \\int_-\\infty^+\\infty[\\int_-\\infty^+\\inftyx(\\tau)h(t-\\tau)d\\tau]e^-jwtdt
Y(jw)=∫−∞+∞[∫−∞+∞x(τ)h(t−τ)dτ]e−jwtdt
交换积分次序,且由于
x
(
τ
)
x(\\tau)
x(τ)与
t
t
t无关
= ∫ − ∞ + ∞ x ( τ ) [ ∫ − ∞ + ∞ h ( t − τ ) e − j w t d t ] d τ = \\int_-\\infty^+\\inftyx(\\tau)[\\int_-\\infty^+\\inftyh(t-\\tau)e^-jwtdt]d\\tau =∫−∞+∞x(τ)[∫−∞+∞h(t−τ)e−jwtdt]dτ
根据傅里叶变换的时移性质:
若
x
(
t
)
x(t)
x(t)的傅里叶变换为
X
(
j
w
)
X(jw)
X(jw),则
x
(
t
−
τ
)
x(t-\\tau)
x(t−τ)的傅里叶变换为:
∫
−
∞
+
∞
x
(
t
−
τ
)
e
−
j
w
t
d
t
=
∫
−
∞
+
∞
x
(
t
−
τ
)
e
−
j
w
(
t
−
τ
)
e
−
j
w
τ
d
t
=
e
−
j
w
τ
X
(
j
w
)
\\int_-\\infty^+\\inftyx(t-\\tau)e^-jwtdt = \\int_-\\infty^+\\inftyx(t-\\tau)e^-jw(t-\\tau)e^-jw\\taudt=e^-jw\\tauX(jw)
∫−∞+∞x(t−τ)e−jwtdt=∫−∞+∞x(t−τ)e−jw(t−τ)e−jwτdt=e−jwτX(jw)
因此,上式中方括号内的部分就可以用时移定理处理。
= ∫ − ∞ + ∞ x ( τ ) [ e − j w τ H ( j w ) ] d τ = \\int_-\\infty^+\\inftyx(\\tau)[e^-jw\\tauH(jw)]d\\tau =∫−∞+∞x(τ)[e−jwτH(jw)]dτ
且 H ( j w ) H(jw) H(jw)与 τ \\tau τ无关,可移出积分外。
= H ( j w ) ∫ − ∞ + ∞ x ( τ ) e − j w τ d τ = H ( j w ) X ( j w ) = H(jw)\\int_-\\infty^+\\inftyx(\\tau)e^-jw\\taud\\tau = H(jw)X(jw) =H(jw)∫−∞+∞x(τ)e−jwτdτ=H(jw)X(jw)
故而
y
(
t
)
=
x
(
t
)
∗
h
(
t
)
y(t) = x(t) * h(t)
y(t)=x(t)∗h(t)
的傅里叶变换为
Y
(
w
)
=
X
(
j
w
)
H
(
j
w
)
Y(w) = X(jw)H(jw)
Y(w)=X(jw)H(jw)
对于频域卷积的情况,由于情况是对称的,所以不再单独推导。
2. 采样定理推导
之前的结论是,对于采样过程,可以写成
x
p
(
t
)
=
x
(
t
)
p
(
t
)
x_p(t) = x(t)p(t)
xp(t)=x(t)p(t)
那么,对于 x p ( t ) x_p(t) xp(t)的傅里叶变换 X p ( j w ) X_p(jw) Xp(jw),就是频域卷积 X ( j w ) ∗ P ( j w ) X(jw)*P(jw) X(jw)∗P(j