抽样定理是啥？？

Posted 2023-04-25

在线等答案

抽样定理是通信理论中的一个重要定理，是模拟信号数字化的理论依据，包括时域抽样定理和频域抽样定理两部分。

采样过程所应遵循的规律，又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系，是连续信号离散化的基本依据。采样定理是1928年由美国电信工程师H.奈奎斯特首先提出来的，因此称为奈奎斯特采样定理。1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理，因此在苏联文献中称为科捷利尼科夫采样定理。

扩展资料

在进行模拟/数字信号的转换过程中，当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，一般实际应用中保证采样频率为信号最高频率的2.56～4倍；采样定理又称奈奎斯特定理。

如果对信号的其它约束是已知的，则当不满足采样率标准时，完美重建仍然是可能的。 在某些情况下（当不满足采样率标准时），利用附加的约束允许近似重建。 这些重建的保真度可以使用Bochner定理来验证和量化。

参考资料来源：百度百科-抽样定理

参考技术A 是对时间连续的信号隔一定的时间抽取一个瞬时幅度值，抽样是由抽样门完成的。解决了为什么可以用数字信号处理的手段解决连续信号与系统在实际应用中遇到的难题 参考技术B 抽取一些样本来研究，为它定下一些理论，或研究后的发现~ 参考技术C 将时间上连续的模拟信号变成一系列时间上离散抽样值的过程称为抽样。从信息还原的角度考虑，对抽样的要求是在用时间离散的抽样序列来代替原模拟信号时，所得的样值序列中能包含原模拟信号的全部信息，这样就可以根据它不失真地恢复出原模拟信号。要满足这一要求，对模拟信号进行抽样的速率就必须达到一定的频率，这便是著名的奈奎斯特抽样定理所表述的主要思想。它是模拟信号数字化的理论基础，简称抽样定理。 参考技术D 抽样定理
定义:在一个频带限制在（0，f h）内的时间连续信号f（t），如果以1/2 f h的时间间隔对它进行抽样，那么根据这些抽样值就能完全恢复原信号。或者说，如果一个连续信号f（t）的频谱中最高频率不超过f h，当抽样频率f S≥2 f h时，抽样后的信号就包含原连续的全部信息。抽样定理在实际应用中应注意在抽样前后模拟信号进行滤波，把高于二分之一抽样频率的频率滤掉。这是抽样中必不可少的步骤。本回答被提问者采纳

中心极限定理|z分布|t分布|卡方分布

生物统计学

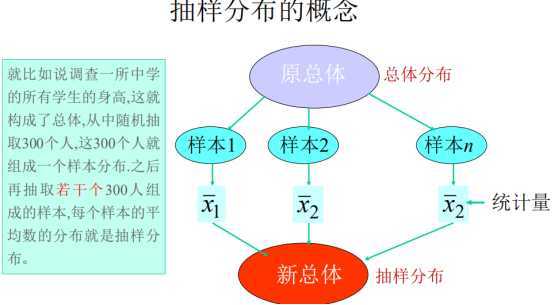
抽样分布：n个样本会得到n个统计量，将这n个统计量作为总体，该总体的分布即是抽样分布

 

 

 

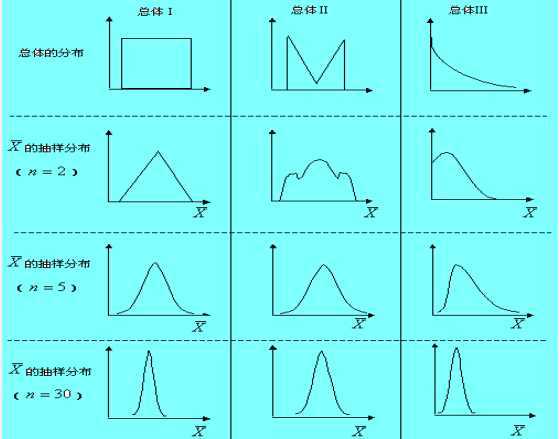
根据辛钦大数定律，从一个非正态分布的总体中抽取的含量主n的样本，当n充分大时，样本平均数渐近服从正态分布。因此平均数的抽样分布对正态性的要求并不是十分严格，但方差的抽样分布，对总体的正态性的要求是十分严格的。

 

样本平均值的分布：

 

 

 

 

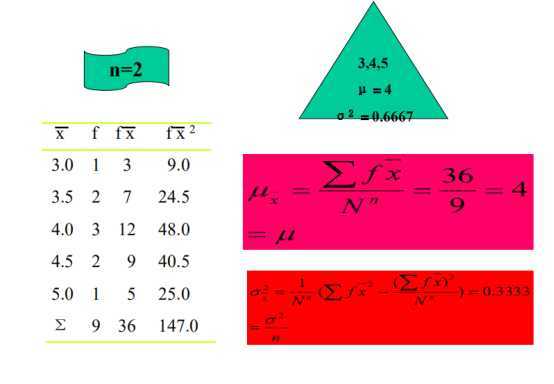
基于正态总体(两个参数都知道)的抽样分布:

eg‘：总体n=3,

因为n=2有放回抽样,有9种可能性：

 

 

 

n=4有放回抽样,有81种可能性

 

 

 

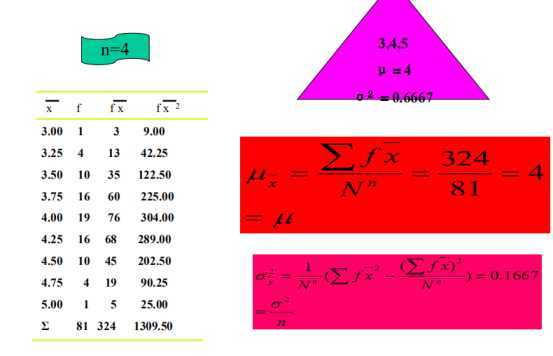
统计量与总体参数不完全一样，但是满足以上关系，所以有：

 

 

 

 

标准误就是参数方差

非正态分布总体(两个参数都知道)：根据中心极限定理，大样本同基于正态总体

所以，只要是大样本都会满足z分布，z即满足N(0,1)

 

 

 

 

方差未知：用样本标准差代替总体标准差，并得到t,此时是t满足自由度为（n-1）的t分布，从PDF可知t分布只与自由度有关，与其他无关。

 

 

 

 

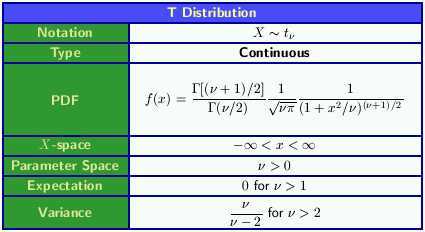
因为n个数要满足均数，必有一个数的值受其他数影响，又因为自由度是独立观测的个数，所以自由度为n-1：

当自由度较大时，也就是n较大时就是正态分布；t--->u

特征值：

 

 

 

 

总体分布和抽样分布的关系：

 

 

 

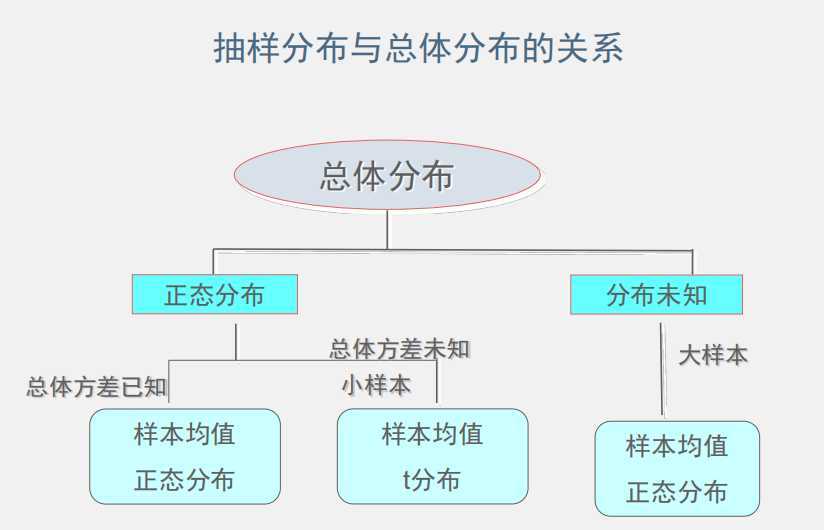
PS：对于总体分布未知的小样本并无方法

 

样本方差的分布

 

正态总体时，两个参数都知道的情况下，样本方差满足卡方分布

 

 

 

随机变量是S方，所以卡方也是一个随机变量，卡方分布只与自由度有关系。

 

总结：

 

 

 

 

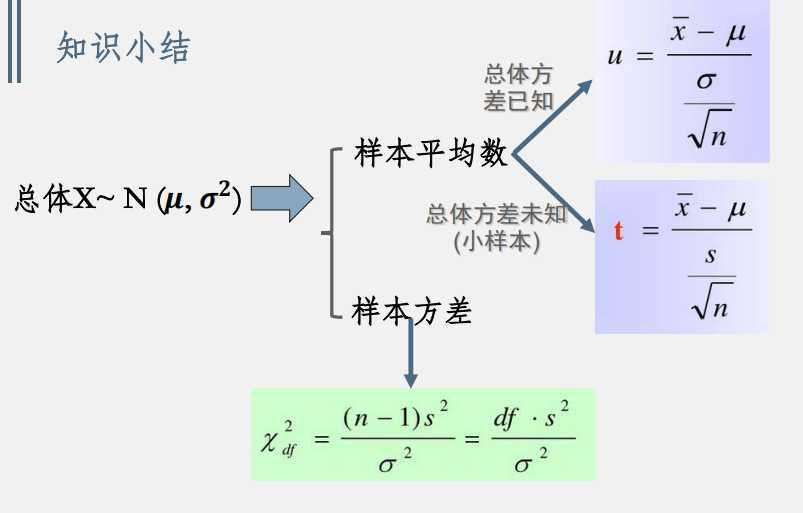
两个正态分布总体（都知道均数和方差），两个样本平均数的和与差的分布：利用正态分布加加减减

 

 

 

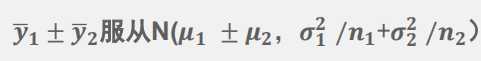
两个正态分布总体（都知道均数，但未知方差具体值，但知道方差相等），两个样本平均数的和与差的分布：利用他分布加加减减

 

 

 

 

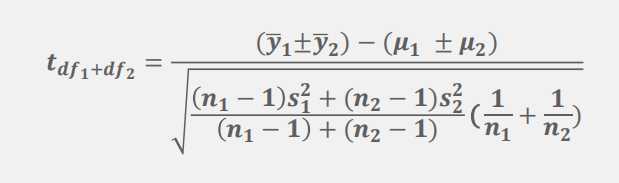
分布使用条件：1.均值是否已知？2.方差是否已知？3.样本量是大或者小？