读SQL进阶教程笔记12_地址与三值逻辑

Posted 2023-04-19 躺柒

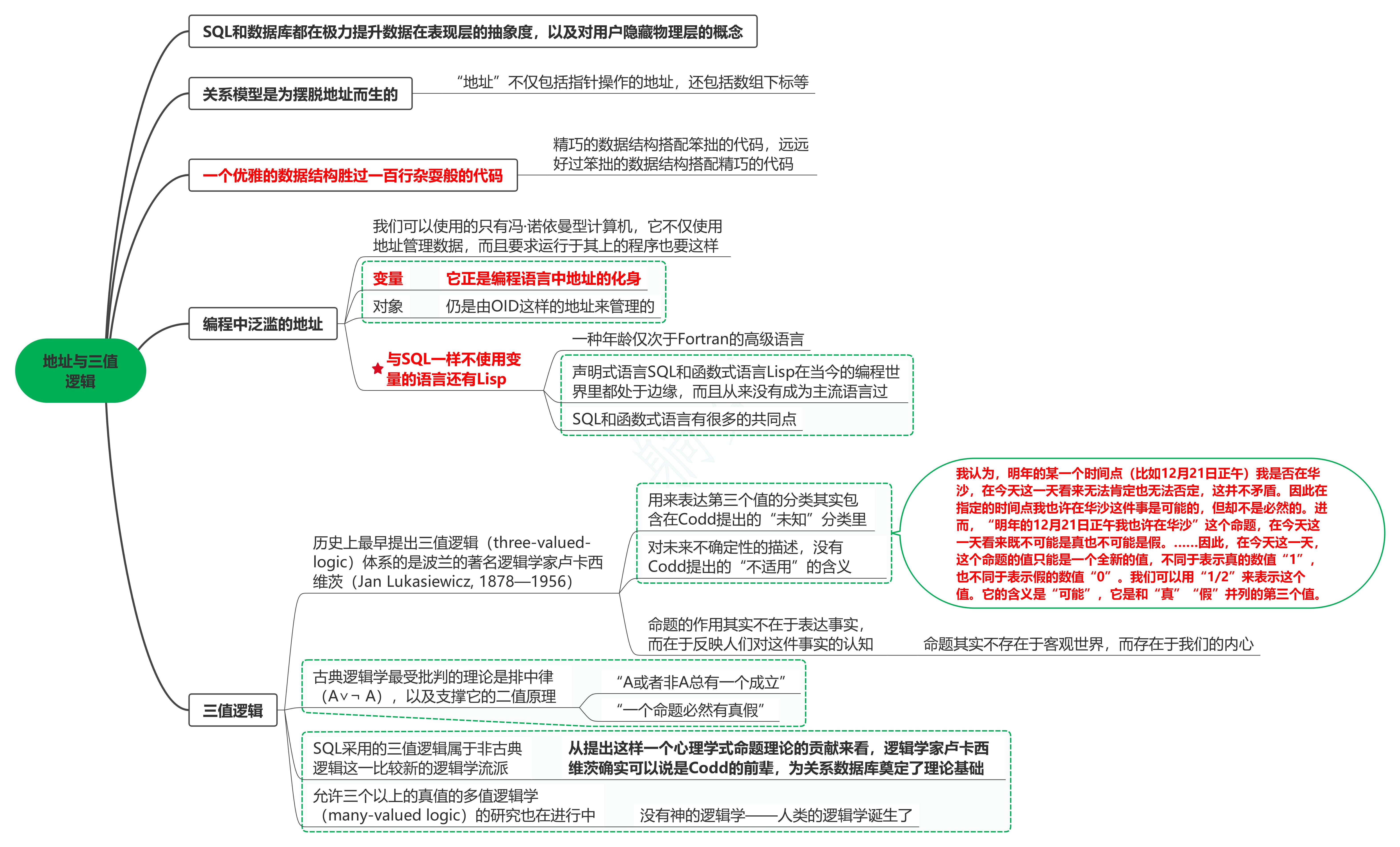
1. SQL和数据库都在极力提升数据在表现层的抽象度，以及对用户隐藏物理层的概念

2. 关系模型是为摆脱地址而生的

2.1. “地址”不仅包括指针操作的地址，还包括数组下标等

3. 一个优雅的数据结构胜过一百行杂耍般的代码

3.1. 精巧的数据结构搭配笨拙的代码，远远好过笨拙的数据结构搭配精巧的代码

4. 编程中泛滥的地址

4.1. 我们可以使用的只有冯·诺依曼型计算机，它不仅使用地址管理数据，而且要求运行于其上的程序也要这样

4.2. 变量

4.2.1. 它正是编程语言中地址的化身

4.3. 对象

4.3.1. 仍是由OID这样的地址来管理的

4.4. 与SQL一样不使用变量的语言还有Lisp

4.4.1. 一种年龄仅次于Fortran的高级语言

4.4.2. 声明式语言SQL和函数式语言Lisp在当今的编程世界里都处于边缘，而且从来没有成为主流语言过

4.4.3. SQL和函数式语言有很多的共同点

5. 三值逻辑

5.1. 历史上最早提出三值逻辑（three-valued-logic）体系的是波兰的著名逻辑学家卢卡西维茨（Jan Lukasiewicz, 1878—1956）

5.1.1. 用来表达第三个值的分类其实包含在Codd提出的“未知”分类里

5.1.2. 对未来不确定性的描述，没有Codd提出的“不适用”的含义

5.1.3. 我认为，明年的某一个时间点（比如12月21日正午）我是否在华沙，在今天这一天看来无法肯定也无法否定，这并不矛盾。因此在指定的时间点我也许在华沙这件事是可能的，但却不是必然的。进而，“明年的12月21日正午我也许在华沙”这个命题，在今天这一天看来既不可能是真也不可能是假。……因此，在今天这一天，这个命题的值只能是一个全新的值，不同于表示真的数值“1”，也不同于表示假的数值“0”。我们可以用“1/2”来表示这个值。它的含义是“可能”，它是和“真”“假”并列的第三个值。

5.1.4. 命题的作用其实不在于表达事实，而在于反映人们对这件事实的认知

5.1.4.1. 命题其实不存在于客观世界，而存在于我们的内心

5.2. 古典逻辑学最受批判的理论是排中律（A∨¬ A），以及支撑它的二值原理

5.2.1. “A或者非A总有一个成立”

5.2.2. “一个命题必然有真假”

5.3. SQL采用的三值逻辑属于非古典逻辑这一比较新的逻辑学流派

5.3.1. 从提出这样一个心理学式命题理论的贡献来看，逻辑学家卢卡西维茨确实可以说是Codd的前辈，为关系数据库奠定了理论基础

5.4. 允许三个以上的真值的多值逻辑学（many-valued logic）的研究也在进行中

5.4.1. 没有神的逻辑学——人类的逻辑学诞生了

读SQL进阶教程笔记10_HAVING下

1. 按照现在的SQL标准来说，HAVING子句是可以单独使用的

1.1. 就不能在SELECT子句里引用原来的表里的列了

1.1.1. 使用常量

1.1.2. 使用聚合函数

1.2. WHERE子句用来调查集合元素的性质，而HAVING子句用来调查集合本身的性质

2. 表不是文件，记录也没有顺序，所以SQL不进行排序

3. GROUP BY子句可以用来生成子集

3.1. SQL通过不断生成子集来求得目标集合

3.2. SQL不是面向过程语言，没有循环、条件分支、赋值操作

3.3. SQL通过不断生成子集来求得目标集合

3.4. SQL不像面向过程语言那样通过画流程图来思考问题，而是通过画集合的关系图来思考

4. 示例

4.1. -- 查询缺失编号的最小值

    SELECT MIN(seq + 1) AS gap
      FROM SeqTbl
     WHERE (seq+ 1) NOT IN ( SELECT seq FROM SeqTbl);

5. 求众数

5.1. 在群体中出现次数最多的值

5.2. 示例

5.2.1.

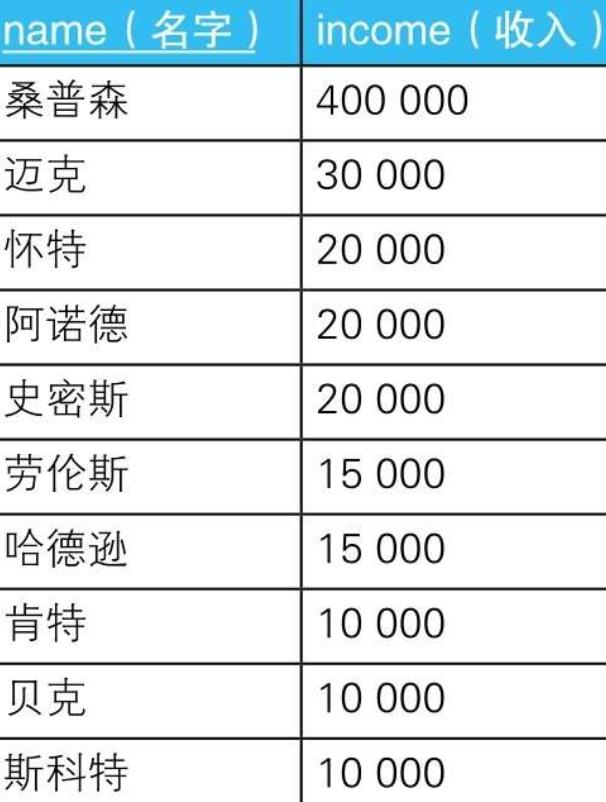
5.2.1.1. --求众数的SQL语句(1)：使用谓词

    SELECT income, COUNT(＊) AS cnt
      FROM Graduates
     GROUP BY income
    HAVING COUNT(＊) ＞= ALL ( SELECT COUNT(＊)
                              FROM Graduates
                              GROUP BY income);

5.2.1.1.1. ALL谓词用于NULL或空集时会出现问题

5.2.1.2. --求众数的SQL语句(2)：使用极值函数

    SELECT income, COUNT(＊) AS cnt
      FROM Graduates
     GROUP BY income
    HAVING COUNT(＊) ＞=  ( SELECT MAX(cnt)
                            FROM ( SELECT COUNT(＊) AS cnt
                                    FROM Graduates
                                  GROUP BY income) TMP ) ;

5.2.1.2.1. 用极值函数来代替

6. 求中位数

6.1. 将集合中的元素按升序排列后恰好位于正中间的元素

6.2. 如果集合的元素个数为偶数，则取中间两个元素的平均值作为中位数

6.3. 示例

6.3.1. --求中位数的SQL语句：在HAVING子句中使用非等值自连接

    SELECT AVG(DISTINCT income)
      FROM (SELECT T1.income
              FROM Graduates T1, Graduates T2
            GROUP BY T1.income
            --S1的条件
      HAVING SUM(CASE WHEN T2.income ＞= T1.income THEN 1 ELSE 0 END)
                ＞= COUNT(＊) / 2
            --S2的条件
        AND SUM(CASE WHEN T2.income ＜= T1.income THEN 1 ELSE 0 END)
                ＞= COUNT(＊) / 2 ) TMP;

6.3.1.1. 加上等号并不是为了清晰地分开子集S1和S2，而是为了让这2个子集拥有共同部分

6.3.1.2. 如果去掉等号，将条件改成“＞COUNT(＊)/2”，那么当元素个数为偶数时，S1和S2就没有共同的元素了，也就无法求出中位数了

6.3.1.3. 如果事先知道集合的元素个数是奇数，那么因为FROM子句里的子查询结果只有一条数据，所以外层的AVG函数可以去掉

7. 查询不包含NULL的集合

7.1. COUNT（＊）和COUNT（列名）

7.1.1. 性能上的区别

7.1.2. COUNT（＊）可以用于NULL

7.1.3. COUNT（列名）与其他聚合函数一样，要先排除掉NULL的行再进行统计

7.1.4. COUNT（＊）查询的是所有行的数目，而COUNT（列名）查询的则不一定是

7.2. 示例1

7.2.1. --在对包含NULL的列使用时，COUNT（＊）和COUNT（列名）的查询结果是不同的

    SELECT COUNT(＊), COUNT(col_1)
      FROM NullTbl;

7.3. 示例2

7.3.1.

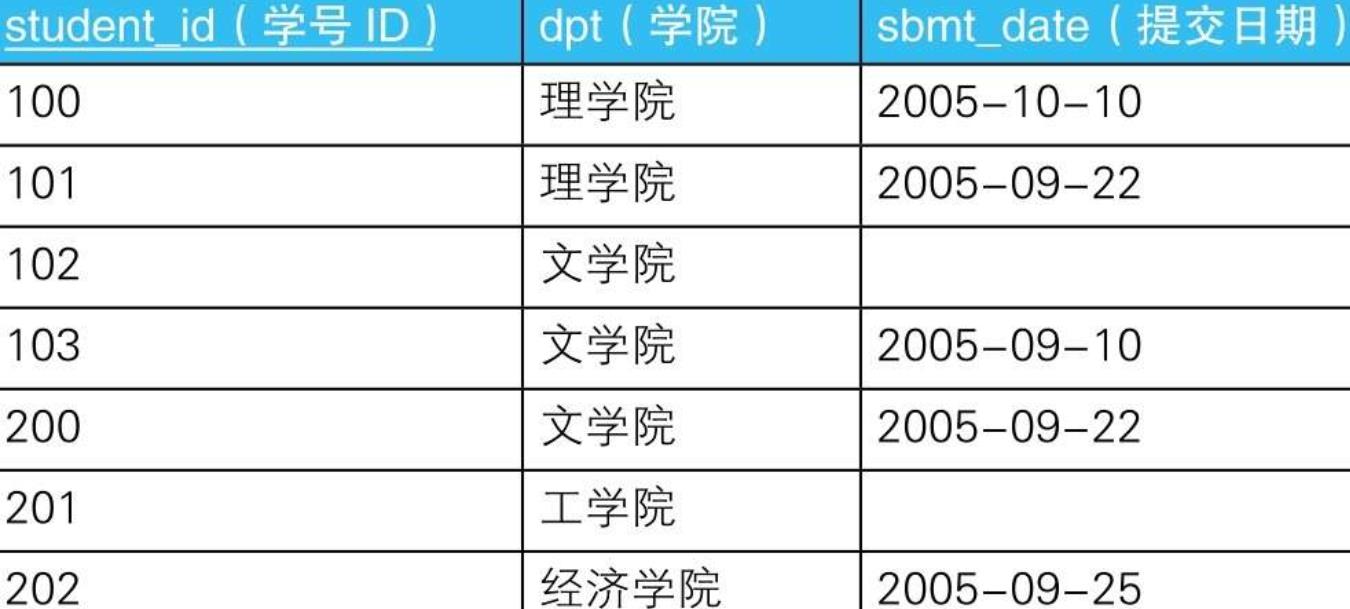
7.3.1.1. --查询“提交日期”列内不包含NULL的学院(1)：使用COUNT函数

    SELECT dpt
      FROM Students
     GROUP BY dpt
    HAVING COUNT(＊) = COUNT(sbmt_date);

7.3.1.2. --查询“提交日期”列内不包含NULL的学院(2)：使用CASE表达式

    SELECT dpt
      FROM Students
     GROUP BY dpt
    HAVING COUNT(＊) = SUM(CASE WHEN sbmt_date IS NOT NULL
                              THEN 1
                              ELSE 0 END);

7.3.1.2.1. CASE表达式的作用相当于进行判断的函数，用来判断各个元素（=行）是否属于满足了某种条件的集合

7.3.1.2.1.1. 特征函数（characteristic function）

8. 关系除法运算

8.1. 示例1

8.1.1.

8.1.2. --查询啤酒、纸尿裤和自行车同时在库的店铺：错误的SQL语句

    SELECT DISTINCT shop
      FROM ShopItems
     WHERE item IN (SELECT item FROM Items);

8.1.2.1. --查询啤酒、纸尿裤和自行车同时在库的店铺：正确的SQL语句

    SELECT SI.shop
      FROM ShopItems SI, Items I
     WHERE SI.item = I.item
     GROUP BY SI.shop
    HAVING COUNT(SI.item) = (SELECT COUNT(item) FROM Items);

8.1.2.1.1. HAVING子句的子查询(SELECT COUNT(item) FROM Items)的返回值是常量3

8.1.3. 带余除法”（division with a remainder）

8.2. 示例2

8.2.1. “精确关系除法”（exact relational division）

8.2.2. --精确关系除法运算：使用外连接和COUNT函数

    SELECT SI.shop
      FROM ShopItems SI LEFT OUTER JOIN Items I
        ON SI.item=I.item
     GROUP BY SI.shop
    HAVING COUNT(SI.item) = (SELECT COUNT(item) FROM Items)    --条件1
      AND COUNT(I.item)  = (SELECT COUNT(item) FROM Items);   --条件2

8.3. 在SQL里，交叉连接相当于乘法运算

8.3.1. 关系除法运算是关系代数中知名度最低的运算