读SQL进阶教程笔记15_SQL编程思维
Posted 躺柒
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了读SQL进阶教程笔记15_SQL编程思维相关的知识,希望对你有一定的参考价值。
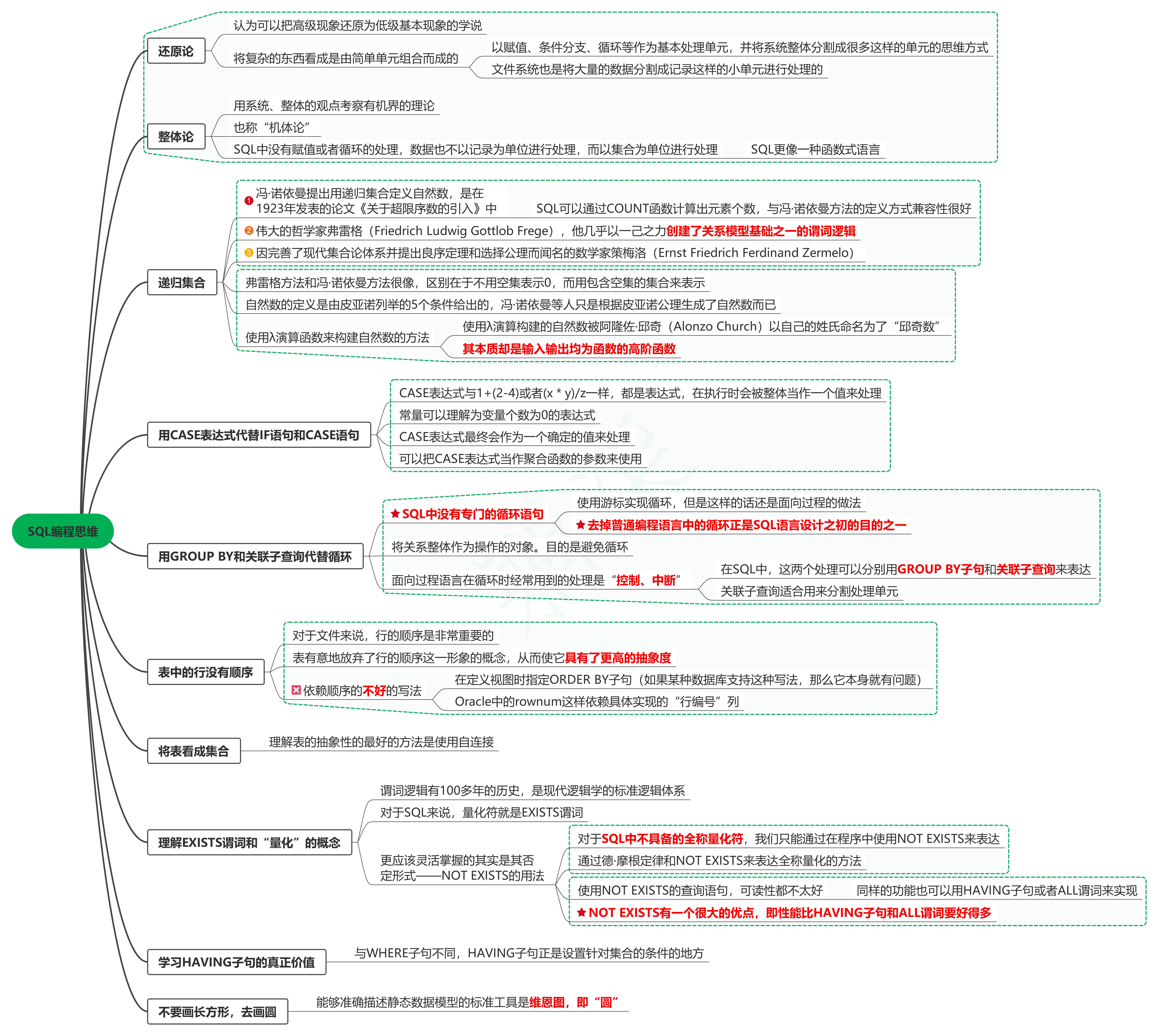
1. 还原论
1.1. 认为可以把高级现象还原为低级基本现象的学说
1.2. 将复杂的东西看成是由简单单元组合而成的
1.2.1. 以赋值、条件分支、循环等作为基本处理单元,并将系统整体分割成很多这样的单元的思维方式
1.2.2. 文件系统也是将大量的数据分割成记录这样的小单元进行处理的
2. 整体论
2.1. 用系统、整体的观点考察有机界的理论
2.2. 也称“机体论”
2.3. SQL中没有赋值或者循环的处理,数据也不以记录为单位进行处理,而以集合为单位进行处理
2.3.1. SQL更像一种函数式语言
3. 递归集合
3.1. 冯·诺依曼提出用递归集合定义自然数,是在1923年发表的论文《关于超限序数的引入》中
3.1.1. SQL可以通过COUNT函数计算出元素个数,与冯·诺依曼方法的定义方式兼容性很好
3.2. 伟大的哲学家弗雷格(Friedrich Ludwig Gottlob Frege),他几乎以一己之力创建了关系模型基础之一的谓词逻辑
3.3. 因完善了现代集合论体系并提出良序定理和选择公理而闻名的数学家策梅洛(Ernst Friedrich Ferdinand Zermelo)
3.4. 弗雷格方法和冯·诺依曼方法很像,区别在于不用空集表示0,而用包含空集的集合来表示
3.5. 自然数的定义是由皮亚诺列举的5个条件给出的,冯·诺依曼等人只是根据皮亚诺公理生成了自然数而已
3.6. 使用λ演算函数来构建自然数的方法
3.6.1. 使用λ演算构建的自然数被阿隆佐·邱奇(Alonzo Church)以自己的姓氏命名为了“邱奇数”
3.6.2. 其本质却是输入输出均为函数的高阶函数
4. 用CASE表达式代替IF语句和CASE语句
4.1. CASE表达式与1+(2-4)或者(x*y)/z一样,都是表达式,在执行时会被整体当作一个值来处理
4.2. 常量可以理解为变量个数为0的表达式
4.3. CASE表达式最终会作为一个确定的值来处理
4.4. 可以把CASE表达式当作聚合函数的参数来使用
5. 用GROUP BY和关联子查询代替循环
5.1. SQL中没有专门的循环语句
5.1.1. 使用游标实现循环,但是这样的话还是面向过程的做法
5.1.2. 去掉普通编程语言中的循环正是SQL语言设计之初的目的之一
5.2. 将关系整体作为操作的对象。目的是避免循环
5.3. 面向过程语言在循环时经常用到的处理是“控制、中断”
5.3.1. 在SQL中,这两个处理可以分别用GROUP BY子句和关联子查询来表达
5.3.2. 关联子查询适合用来分割处理单元
6. 表中的行没有顺序
6.1. 对于文件来说,行的顺序是非常重要的
6.2. 表有意地放弃了行的顺序这一形象的概念,从而使它具有了更高的抽象度
6.3. 依赖顺序的不好的写法
6.3.1. 在定义视图时指定ORDER BY子句(如果某种数据库支持这种写法,那么它本身就有问题)
6.3.2. Oracle中的rownum这样依赖具体实现的“行编号”列
7. 将表看成集合
7.1. 理解表的抽象性的最好的方法是使用自连接
8. 理解EXISTS谓词和“量化”的概念
8.1. 谓词逻辑有100多年的历史,是现代逻辑学的标准逻辑体系
8.2. 对于SQL来说,量化符就是EXISTS谓词
8.3. 更应该灵活掌握的其实是其否定形式——NOT EXISTS的用法
8.3.1. 对于SQL中不具备的全称量化符,我们只能通过在程序中使用NOT EXISTS来表达
8.3.2. 通过德·摩根定律和NOT EXISTS来表达全称量化的方法
8.3.3. 使用NOT EXISTS的查询语句,可读性都不太好
8.3.3.1. 同样的功能也可以用HAVING子句或者ALL谓词来实现
8.3.4. NOT EXISTS有一个很大的优点,即性能比HAVING子句和ALL谓词要好得多
9. 学习HAVING子句的真正价值
9.1. 与WHERE子句不同,HAVING子句正是设置针对集合的条件的地方
10. 不要画长方形,去画圆
10.1. 能够准确描述静态数据模型的标准工具是维恩图,即“圆”
读SQL进阶教程笔记09_HAVING上

1. HAVING子句的用法
1.1. 学习SQL时最大的阻碍就是我们已经习惯了的面向过程语言的思考方式(排序、循环、条件分支、赋值等)
1.2. 只有习惯了面向集合的思考方式,才能真正地学好它
1.3. 帮助我们顺利地忘掉面向过程语言的思考方式并理解SQL面向集合特性的最为有效的方法
1.4. HAVING子句的处理对象是集合而不是记录
1.4.1. 如果一个实体对应着一行数据→那么就是元素,所以使用WHERE子句
1.4.2. 如果一个实体对应着多行数据→那么就是集合,所以使用HAVING子句
1.5. HAVING子句可以通过聚合函数(特别是极值函数)针对集合指定各种条件
1.5.1.

1.5.2. 如果通过CASE表达式生成特征函数,那么无论多么复杂的条件都可以描述
2. 点名
2.1. 示例
2.1.1.

2.1.1.1. -- 用谓词表达全称量化命题
SELECT team_id, member
FROM Teams T1
WHERE NOT EXISTS
(SELECT *
FROM Teams T2
WHERE T1.team_id = T2.team_id
AND status <>’待命’);
2.1.1.1.1. “所有队员都处于待命状态”=“不存在不处于待命状态的队员”
2.1.1.1.2. 查询性能很好
2.1.1.1.3. 结果中能体现出队员信息
2.1.1.2. -- 用集合表达全称量化命题(1)
SELECT team_id
FROM Teams
GROUP BY team_id
HAVING COUNT(*) = SUM(CASE WHEN status =’待命’
THEN 1
ELSE 0 END);
2.1.1.2.1. 代码很简洁
2.1.1.2.2. 使用的是特征函数的方法
2.1.1.3. -- 用集合表达全称量化命题(2)
SELECT team_id
FROM Teams
GROUP BY team_id
HAVING MAX(status) =’待命’
AND MIN(status) =’待命’;
2.1.1.3.1. 性能更好
2.1.1.3.1.1. 极值函数可以使用参数字段的索引
2.1.1.3.2. 如果元素最大值和最小值相等,那么这个集合中肯定只有一种值
2.1.1.4. -- 列表显示各个队伍是否所有队员都在待命
SELECT team_id,
CASE WHEN MAX(status) =’待命’AND MIN(status) =’待命’
THEN ’全都在待命’
ELSE’队长!人手不够’END AS status
FROM Teams
GROUP BY team_id;
2.1.1.4.1. 条件移到SELECT子句后,查询可能就不会被数据库优化了
3. 单重集合
3.1. 示例
3.1.1.
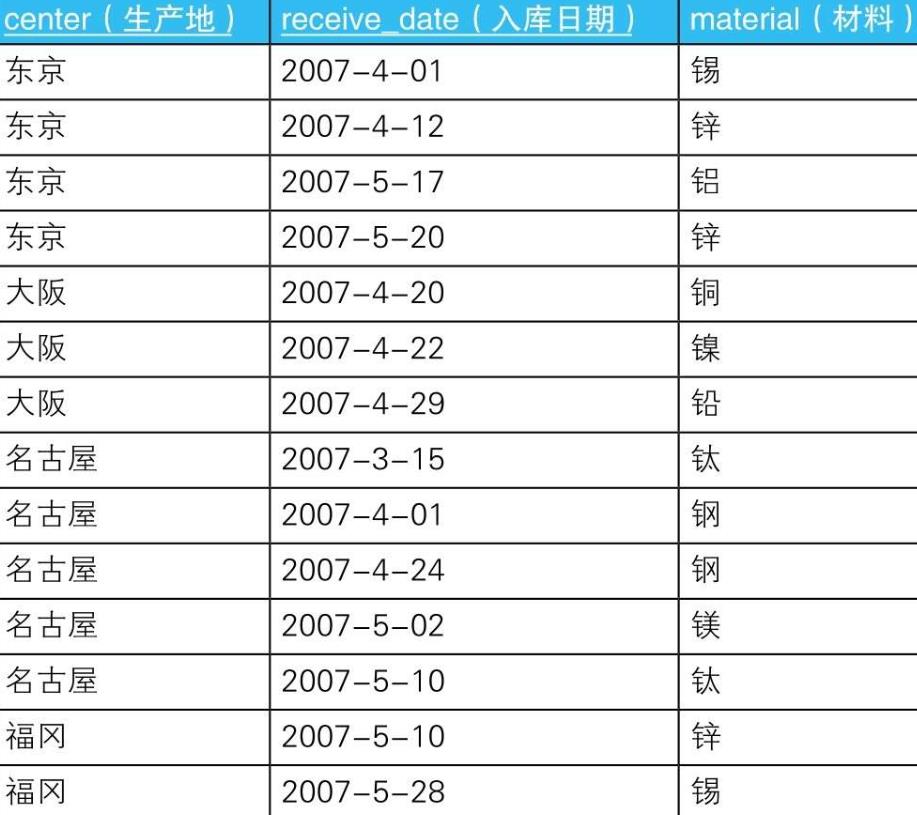
3.1.1.1. -- 选中材料存在重复的生产地
SELECT center
FROM Materials
GROUP BY center
HAVING COUNT(material) <> COUNT(DISTINCT material);
3.1.1.1.1.
SELECT center,
CASE WHEN COUNT(material) <> COUNT(DISTINCT material) THEN’存在重复’
ELSE’不存在重复’END AS status
FROM Materials
GROUP BY center;
3.1.1.2. --存在重复的集合:使用EXISTS
SELECT center, material
FROM Materials M1
WHERE EXISTS
(SELECT *
FROM Materials M2
WHERE M1.center = M2.center
AND M1.receive_date <> M2.receive_date
AND M1.material = M2.material);
3.2. 在数学中,通过GROUP BY生成的子集有一个对应的名字,叫作划分(partition)
3.2.1. 集合论和群论中的重要概念,指的是将某个集合按照某种规则进行分割后得到的子集
3.2.2. 这些子集相互之间没有重复的元素,而且它们的并集就是原来的集合
4. 寻找缺失的编号:升级版
4.1. 示例
4.1.1. -- 如果有查询结果,说明存在缺失的编号
SELECT’存在缺失的编号’AS gap
FROM SeqTbl
HAVING COUNT(*) <> MAX(seq);
4.1.1.1. 有一个前提条件,即数列的起始值必须是1
4.1.2. -- 如果有查询结果,说明存在缺失的编号:只调查数列的连续性
SELECT’存在缺失的编号’ AS gap
FROM SeqTbl
HAVING COUNT(*) <> MAX(seq) - MIN(seq) + 1 ;
4.1.3. -- 不论是否存在缺失的编号都返回一行结果
SELECT CASE WHEN COUNT(*) = 0
THEN ’表为空’
WHEN COUNT(*) <> MAX(seq) - MIN(seq) + 1
THEN ’存在缺失的编号’
ELSE’连续’END AS gap
FROM SeqTbl;
4.1.4. -- 查找最小的缺失编号:表中没有1时返回1
SELECT CASE WHEN COUNT(*) = 0 OR MIN(seq) > 1 -- 最小值不是1时→返回1
THEN 1
ELSE (SELECT MIN(seq +1) -- 最小值是1时→返回最小的缺失编号
FROM SeqTbl S1
WHERE NOT EXISTS
(SELECT *
FROM SeqTbl S2
WHERE S2.seq = S1.seq + 1)) END
FROM SeqTbl;
5. 为集合设置详细的条件
5.1. 示例
5.1.1.
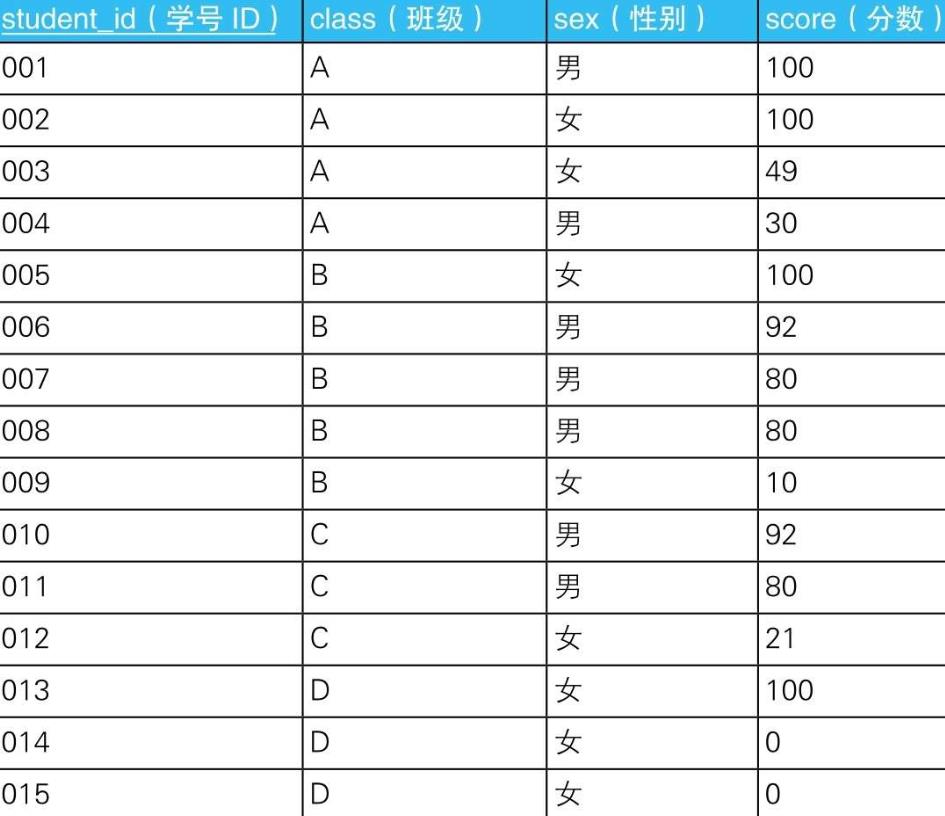
5.1.1.1. 查询出75%以上的学生分数都在80分以上的班级
5.1.1.1.1.
SELECT class
FROM TestResults
GROUP BY class
HAVING COUNT(*) * 0.75
<= SUM(CASE WHEN score >= 80
THEN 1
ELSE 0 END) ;
5.1.1.2. 查询出分数在50分以上的男生的人数比分数在50分以上的女生的人数多的班级
5.1.1.2.1.
SELECT class
FROM TestResults
GROUP BY class
HAVING SUM(CASE WHEN score >= 50 AND sex =’男’
THEN 1
ELSE 0 END)
> SUM(CASE WHEN score >= 50 AND sex =’女’
THEN 1
ELSE 0 END) ;
5.1.1.3. 查询出女生平均分比男生平均分高的班级
5.1.1.3.1. -- 比较男生和女生平均分的SQL语句(1):对空集使用AVG后返回0
SELECT class
FROM TestResults
GROUP BY class
HAVING AVG(CASE WHEN sex =’男’
THEN score
ELSE 0 END)
< AVG(CASE WHEN sex =’女’
THEN score
ELSE 0 END) ;
5.1.1.3.2. -- 比较男生和女生平均分的SQL语句(2):对空集求平均值后返回NULL
SELECT class
FROM TestResults
GROUP BY class
HAVING AVG(CASE WHEN sex =’男’
THEN score
ELSE NULL END)
< AVG(CASE WHEN sex =’女’
THEN score
ELSE NULL END) ;
5.1.1.3.2.1. 根据标准SQL的定义,对空集使用AVG函数时,结果会返回NULL
以上是关于读SQL进阶教程笔记15_SQL编程思维的主要内容,如果未能解决你的问题,请参考以下文章